W zastosowaniach inżynierskich często spotykamy się z funkcjami, których wartości zmieniają się gwałtownie przy określonych wartościach czasu t. Jednym z powszechnych przykładów jest włączanie lub wyłączanie napięcia w obwodzie elektrycznym przy określonej wartości czasu t.
Dalej, na tej stronie…
Przesunięta funkcja kroku jednostkowego
Puls prostokątny
Wartość t = 0 jest zwykle przyjmowana jako dogodny czas do załączenia lub wyłączenia danego napięcia.
Proces przełączania można opisać matematycznie funkcją zwaną funkcją kroku jednostkowego (zwaną inaczej funkcją Heaviside’a od nazwiska Olivera Heaviside’a).
Funkcja kroku jednostkowego
Definicja: Funkcja kroku jednostkowego, `u(t)`, jest zdefiniowana jako
`u(t)={: {(0, t < 0), (1, t > 0) :}`
To znaczy, że u jest funkcją czasu t, a u ma wartość zero, gdy czas jest ujemny (zanim przerzucimy przełącznik); i wartość jeden, gdy czas jest dodatni (od kiedy przerzucimy przełącznik).
Graph of `f(t)=u(t)`, the unit step function.
Value at t = 0?
W niektórych podręcznikach zobaczysz funkcję unit step zdefiniowaną jako mającą wartość 1 w t = 0, w następujący sposób:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
Na naszym wykresie nieciągłość wskazalibyśmy w ten sposób:
Graph of `f(t)=u(t)`, the unit step function, with `f(0) = 1`.
Czasami można też spotkać się z wartością podaną jako `f(0) = 0.5`.
W tej pracy nie ma to większego znaczenia dla naszych obliczeń, więc będziemy nadal używać pierwszej interpretacji i odpowiednio rysować nasze wykresy.
Przesunięta funkcja kroku jednostkowego
W wielu obwodach przebiegi są stosowane w określonych odstępach czasu innych niż `t=0`. Taką funkcję można opisać za pomocą przesuniętej (lub opóźnionej) funkcji kroku jednostkowego.
Definicja przesuniętej funkcji kroku jednostkowego
Funkcję, która ma wartość `0` do czasu `t = a`, a potem ma wartość `1`, zapisujemy:
`u(t-a)={: (0, if, t < a), (1, if, t > a) :}`
Przykład 1 -. Funkcja o przesuniętym kroku jednostkowym
`f(t) = u(t – 3)`
Wynika z tego równania, że f(t) ma wartość równą f(t). równanie oznacza, że f(t) ma wartość `0`, gdy `t < 3` i `1`, gdy `t > 3`.
Szkic przebiegu jest następujący:
Graph of `f(t)=u(t-3)`, a shifted unit step function.
Puls prostokątny
Powszechną sytuacją w obwodzie jest przyłożenie napięcia w określonym czasie (powiedzmy t = a) i usunięcie go później, w czasie t = b (powiedzmy). Zapisujemy taką sytuację za pomocą funkcji kroku jednostkowego jako:
`V(t) = u(t – a) – u(t – b)`
Napięcie to ma siłę `1`, czas trwania `(b – a)`.
Przykład 2 – Impuls prostokątny
Wykres `V(t) = u(t – 1,2) – u(t – 3,8)` jest następujący. Tutaj czas trwania wynosi `3,8 – 1,2 = 2,6`.
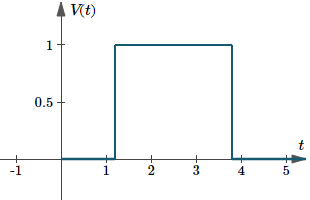
Wykres `V(t)=u(t-1.2)-u(t-3.8)`, przykład impulsu prostokątnego.
Ćwiczenia
Potrzebujesz papieru graficznego?
Zapisz poniższe funkcje w kategoriach funkcji kroku jednostkowego. Naszkicuj każdy przebieg.
(a) Źródło 12 V jest włączone w czasie t = 4 s.
Odpowiedź
Ponieważ napięcie jest włączone w czasie t = 4, musimy użyć u(t – 4). Mnożymy przez 12, ponieważ tyle wynosi napięcie.
Funkcję zapisujemy w następujący sposób:
`V(t)=12-u(t-4)`.
Tutaj wykres:
Graph of `V(t)=12-u(t-4)`, a shifted step function.
(b) `V(t)={: (1, 0 < t < a),(0, t > a) :}`
(Załóżmy, że a > 0.)
Odpowiedź
Słowem, napięcie ma wartość `1` do czasu `t = a`. Następnie zostaje wyłączone.
Mamy sytuację „impulsu prostokątnego” i musimy skorzystać z tego wzoru:
`V(t) = u(t – a) – u(t – b)`
W naszym przykładzie impuls zaczyna się w chwili `t = 0`, więc używamy `u(t)`, a kończy w chwili `t = a`, więc używamy `u(t – a)`.
Więc wymagana funkcja to:
`V(t)=1-` `=u(t)-u(t-a)`
Graph of `V(t)=u(t)-u(t-a)`, a shifted unit step function.
(c) Jeden cykl fali kwadratowej, `f(0) = 4`, amplituda = `4`, okres = `2` sekundy.
Odpowiedź
`f(0) = 4` oznacza, że zaczynamy od wartości `4`.
Jeśli cała fala ma okres `2`, i jest to fala kwadratowa, to znaczy, że przez połowę czasu wartość jest (dodatnia) `4`, a przez drugą połowę jest `-4`.
Więc przez pierwszą sekundę ma wartość `4`, przez drugą sekundę wartość funkcji jest `-4`.
Piszemy to, korzystając ze wzoru na „impuls prostokątny” z wcześniej:
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
Wykres tego pierwszego cyklu to:
Graph of `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, a square wave.
(d) Funkcja Rampa jednostkowa (tj.`f(t) = t` dla `t > 0`)
Odpowiedź
Jednostkowa funkcja rampowa ma nachylenie `1` , zaczynając od `t = 0` i przechodzi przez `(0, 0)`.
Dana jest więc funkcja napięcia:
`V(t) = t – u(t)`
Wykresem funkcji jest:
Graph of `V(t)=t – u(t)`, the unit ramp function.
(e) Jeden cykl fali piłokształtnej (i.e. `f(t)=a/b t` dla `0 < t < b`. Assume `a > 0`.)
Answer
Nasz wykres zaczyna się w punkcie `t = 0` i ma nachylenie `a / b`. Kończy się w punkcie `t = b`.
Więc naszą funkcją będzie:
`f(t)=a/b t – {u(t)-u(t-b)}`
Wykres naszej funkcji:
Graph of `f(t)=a/b t – {u(t)-u(t-b)}`, a sawtooth waveform.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t 5) :}`
Odpowiedź
W tym przykładzie naszą funkcją jest `V(t) = 2t + 8`, która ma nachylenie `2` i punkt przecięcia `V` – 8`.
Sygnał jest włączony tylko pomiędzy `t = 3` i `t = 5`. Przez resztę czasu jest wyłączony.
Więc nasza funkcja napięcia będzie miała postać:
`V(t) `= (2t+8) -{u(t – 3)- u(t – 5)}`
Wykres wygląda następująco:
Graph of `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}`. Linia przerywana to `V(t) = 2t + 8`.
top
Szukaj IntMath
Online Calculus Solver
Ten kalkulator może rozwiązywać szeroki zakres problemów matematycznych.
Przejdź do: Online calculus solver