In der Technik begegnen uns häufig Funktionen, deren Werte sich bei bestimmten Zeitwerten t sprunghaft ändern. Ein häufiges Beispiel ist das Ein- und Ausschalten einer Spannung in einem elektrischen Stromkreis bei einem bestimmten Zeitwert t.
Später, auf dieser Seite…
Verschiebte Einheitsschrittfunktion
Rechteckimpuls
Der Wert t = 0 wird üblicherweise als günstiger Zeitpunkt für das Ein- oder Ausschalten der gegebenen Spannung angenommen.
Der Schaltvorgang kann mathematisch durch die sogenannte Einheitsschrittfunktion (nach Oliver Heaviside auch als Heaviside-Funktion bezeichnet) beschrieben werden.
Die Einheitsschrittfunktion
Definition: Die Einheitsschrittfunktion, `u(t)`, ist definiert als
`u(t)={: {(0, t < 0), (1, t > 0) :}`
Das heißt, u ist eine Funktion der Zeit t, und u hat den Wert Null, wenn die Zeit negativ ist (bevor wir den Schalter umlegen); und den Wert Eins, wenn die Zeit positiv ist (ab dem Umlegen des Schalters).
Graph von `f(t)=u(t)`, der Einheitsschrittfunktion.
Wert bei t = 0?
In manchen Lehrbüchern wird die Einheitsschrittfunktion so definiert, dass sie bei t = 0 den Wert 1 hat, wie folgt:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
Wir würden die Unstetigkeit in unserem Graphen so darstellen:
Graph von `f(t)=u(t)`, der Einheitsschrittfunktion, mit `f(0) = 1`.
Manchmal wird der Wert auch als `f(0) = 0 angegeben.5`.
In dieser Arbeit macht das keinen großen Unterschied für unsere Berechnungen, also werden wir weiterhin die erste Interpretation verwenden und unsere Graphen entsprechend zeichnen.
Verschiebte Einheitsschrittfunktion
In vielen Schaltungen werden Wellenformen in bestimmten Intervallen angelegt, die nicht `t=0` sind. Eine solche Funktion kann mit der verschobenen (auch verzögerten) Einheitsschrittfunktion beschrieben werden.
Definition der verschobenen Einheitsschrittfunktion
Eine Funktion, die bis zum Zeitpunkt `t = a` den Wert `0` hat und danach den Wert `1`, wird geschrieben:
`u(t-a)={: (0, wenn, t < a), (1, wenn, t > a) :}`
Beispiel 1 – Verschobene Einheitsschrittfunktion
`f(t) = u(t – 3)`
Die Gleichung bedeutet, dass f(t) den Wert `0` hat, wenn `t < 3` und `1`, wenn `t > 3`.
Die Skizze der Wellenform sieht wie folgt aus:
Graph von `f(t)=u(t-3)`, einer verschobenen Einheitsschrittfunktion.
Rechteckiger Impuls
Eine häufige Situation in einer Schaltung ist, dass eine Spannung zu einem bestimmten Zeitpunkt (sagen wir t = a) angelegt und später, sagen wir bei t = b, entfernt wird. Wir schreiben eine solche Situation mit Hilfe von Einheitsschrittfunktionen als:
`V(t) = u(t – a) – u(t – b)`
Diese Spannung hat die Stärke `1`, die Dauer `(b – a)`.
Beispiel 2 – Rechteckimpuls
Der Graph von `V(t) = u(t – 1,2) – u(t – 3,8)` sieht wie folgt aus. Hier ist die Dauer `3.8 – 1.2 = 2.6`.
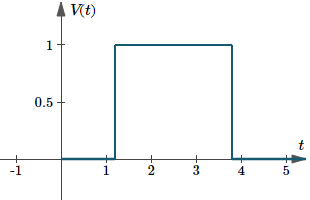
Graph von `V(t)=u(t-1.2)-u(t-3.8)`, ein Beispiel für einen Rechteckimpuls.
Übungen
Brauchen Sie Millimeterpapier?
Schreiben Sie die folgenden Funktionen in Form von Einheitsschrittfunktion(en). Skizzieren Sie jede Wellenform.
(a) Eine 12-V-Quelle wird bei t = 4 s eingeschaltet.
Antwort
Da die Spannung bei t = 4 eingeschaltet wird, müssen wir u(t – 4) verwenden. Wir multiplizieren mit 12, da dies die Spannung ist.
Wir schreiben die Funktion wie folgt:
`V(t)=12-u(t-4)`.
Hier ist der Graph:
Graph von `V(t)=12-u(t-4)`, einer verschobenen Stufenfunktion.
(b) `V(t)={{: (1, 0 < t < a),(0, t > a) :}`
(Angenommen, a > ist 0.)
Antwort
In Worten: Die Spannung hat den Wert `1` bis zum Zeitpunkt `t = a`. Dann wird sie ausgeschaltet.
Wir haben eine „Rechteckimpuls“-Situation und müssen diese Formel verwenden:
`V(t) = u(t – a) – u(t – b)`
In unserem Beispiel beginnt der Impuls bei `t = 0`, also verwenden wir `u(t)`, und endet bei `t = a`, also verwenden wir `u(t – a)`.
Die benötigte Funktion ist also:
`V(t)=1-` `=u(t)-u(t-a)`
Graph von `V(t)=u(t)-u(t-a)`, einer verschobenen Einheitsschrittfunktion.
(c) Ein Zyklus einer Rechteckwelle, `f(0) = 4`, Amplitude = `4`, Periode = `2` Sekunden.
Antwort
`f(0) = 4` bedeutet, wir beginnen beim Wert `4`.
Wenn die ganze Welle die Periode `2` hat und es sich um eine Rechteckwelle handelt, dann bedeutet das, dass für die Hälfte der Zeit der Wert `4` (positiv) ist und für die andere Hälfte `-4`.
So hat sie für die erste Sekunde den Wert `4`, für die zweite Sekunde ist der Funktionswert `-4`.
Wir schreiben das, indem wir die „Rechteckimpuls“-Formel von vorher verwenden:
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
Der Graph dieses ersten Zyklus ist:
Graph von `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, einer Rechteckwelle.
(d) Die Einheitsrampenfunktion (d.h..`f(t) = t` für `t > 0`)
Antwort
Die Einheitsrampenfunktion hat die Steigung `1` , beginnend bei `t = 0` , und geht durch `(0, 0)`.
Die Spannungsfunktion ist also gegeben durch:
`V(t) = t – u(t)`
Der Graph der Funktion ist:
Graph von `V(t)=t – u(t)`, der Einheitsrampenfunktion.
(e) Ein Zyklus einer Sägezahnwellenform (d.d. h. `f(t)=a/b t` für `0 < t < b`. Nehmen Sie `a > 0` an.)
Antwort
Unser Graph beginnt bei `t = 0` und hat die Steigung `a / b`. Er endet bei `t = b`.
So wird unsere Funktion sein:
`f(t)=a/b t – {u(t)-u(t-b)}`
Der Graph unserer Funktion:
Der Graph von `f(t)=a/b t – {u(t)-u(t-b)}`, eine Sägezahn-Wellenform.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t 5) :}`
Antwort
In diesem Beispiel ist unsere Funktion `V(t) = 2t + 8`, die Steigung `2` und `V`-Achsenabschnitt `8` hat.
Das Signal ist nur zwischen `t = 3` und `t = 5` eingeschaltet. Die restliche Zeit ist es ausgeschaltet.
So wird unsere Spannungsfunktion sein:
`V(t) ` `= (2t+8) -{u(t – 3)- u(t – 5)}`
Der Graph sieht wie folgt aus:
Der Graph von `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}`. Die gestrichelte Linie ist `V(t) = 2t + 8`.
top
Online Calculus Solver
Dieser Calculus Solver kann eine Vielzahl von mathematischen Problemen lösen.
Gehen Sie zu: Online-Rechenkernlöser