Lernziele
Am Ende dieses Abschnitts werden Sie in der Lage sein:
- Definieren Sie Äquipotentialflächen und Äquipotentiallinien
- Erläutern Sie den Zusammenhang zwischen Äquipotentiallinien und elektrischen Feldlinien
- Bilden Sie Äquipotentiallinien für eine oder zwei Punktladungen
- Beschreiben Sie das Potential eines Leiters
- Vergleichen und kontrastieren Sie Äquipotentiallinien und Höhenlinien auf topographischen Karten
Wir können elektrische Potentiale (Spannungen) bildlich darstellen,genauso wie wir Bilder zur Veranschaulichung von elektrischen Feldern gezeichnet haben. Das ist nicht verwunderlich, da die beiden Konzepte miteinander verwandt sind. Betrachten wir Abbildung\(\PageIndex{1}\), die eine isolierte positive Punktladung und ihre elektrischen Feldlinien zeigt, die von einer positiven Ladung ausgehen und an negativen Ladungen enden. Wir verwenden blaue Pfeile, um die Größe und Richtung des elektrischen Feldes darzustellen, und wir verwenden grüne Linien, um Orte darzustellen, an denen das elektrische Potential konstant ist. Diese werden in drei Dimensionen als Äquipotentialflächen und in zwei Dimensionen als Äquipotentiallinien bezeichnet. Der Begriff Äquipotential wird auch als Substantiv verwendet und bezieht sich auf eine Äquipotentiallinie oder -fläche. Das Potenzial für eine Punktladung ist überall auf einer imaginären Kugel mit dem Radius r, die die Ladung umgibt, gleich groß. Dies ist wahr, weil das Potenzial für eine Punktladung durch \(V = kq/r\) gegeben ist und somit an jedem Punkt, der einen bestimmten Abstand von der Ladung hat, den gleichen Wert hat. Eine Äquipotentialsphäre ist ein Kreis in der zweidimensionalen Ansicht der Abbildung \(\PageIndex{1}\). Da die elektrischen Feldlinien radial von der Ladung weg zeigen, stehen sie senkrecht zu den Äquipotentiallinien.
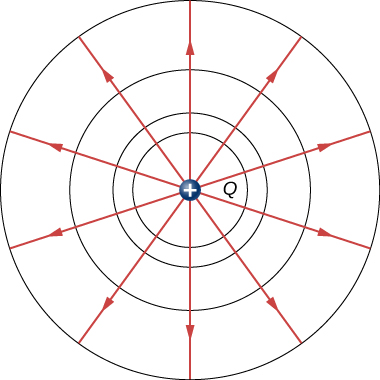
Es ist wichtig zu beachten, dass Äquipotentiallinien immer senkrecht zu elektrischen Feldlinien stehen. Es ist keine Arbeit erforderlich, um eine Ladung entlang eines Äquipotentials zu bewegen, da \(\Delta V = 0\). Somit ist die Arbeit
Die Arbeit ist Null, wenn die Richtung der Kraft senkrecht zur Verschiebung ist. Die Kraft hat die gleiche Richtung wie \(E\), eine Bewegung entlang eines Äquipotentials muss senkrecht zu \(E\) verlaufen. Genauer gesagt, ist die Arbeit mit dem elektrischen Feld verbunden durch
&= q\vec{E} \cdot \vec{d} \Nummer \\ &= qEd\, \cos \, \theta \Nummer \\\ &= 0. \nonumber \end{align}\nonumber\]
Beachten Sie, dass in Gleichung \ref{eq5}, \(E\) und \(F\) die Größen des elektrischen Feldes bzw. der Kraft symbolisieren. Weder \(q\) noch \(E\) ist Null und \(d\) ist auch nicht Null. Also muss \(\cos \,\theta\) 0 sein, was bedeutet, dass \(\theta\) \(90^o\) sein muss. Mit anderen Worten, die Bewegung entlang eines Äquipotentials ist senkrecht zuE.
Eine der Regeln für statische elektrische Felder und Leiter ist, dass das elektrische Feld senkrecht zur Oberfläche eines jeden Leiters sein muss. Dies impliziert, dass ein Leiter in statischen Situationen eine Äquipotentialfläche ist. Es kann keine Spannungsdifferenz über die Oberfläche eines Leiters geben, da sonst Ladungen fließen.Eine der Anwendungen dieser Tatsache ist, dass ein Leiter auf das, was wir als Null Volt betrachten, fixiert werden kann, indem er mit einem guten Leiter an die Erde angeschlossen wird – ein Prozess, der Erdung genannt wird. Die Erdung kann ein nützliches Sicherheitsinstrument sein. Zum Beispiel stellt die Erdung des Metallgehäuses eines elektrischen Geräts sicher, dass es im Verhältnis zur Erde null Volt hat.
Da ein Leiter ein Äquipotential ist, kann er jede Äquipotentialfläche ersetzen. In Abbildung \(\PageIndex{2}\) kann beispielsweise ein geladener kugelförmiger Leiter die Punktladung ersetzen, und das elektrische Feld und die Potenzialflächen außerhalb des Leiters werden verändert, was die Behauptung bestätigt, dass eine kugelförmige Ladungsverteilung einer Punktladung in ihrem Zentrum entspricht.
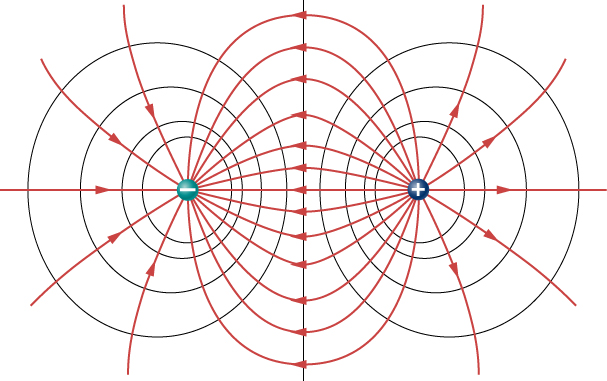
Abbildung \(\PageIndex{2}\) zeigt das elektrische Feld und die Äquipotenziallinien für zwei gleiche und entgegengesetzte Ladungen. Bei gegebenen elektrischen Feldlinien können die Äquipotentiallinien einfach gezeichnet werden, indem man sie senkrecht zu den elektrischen Feldlinien macht.
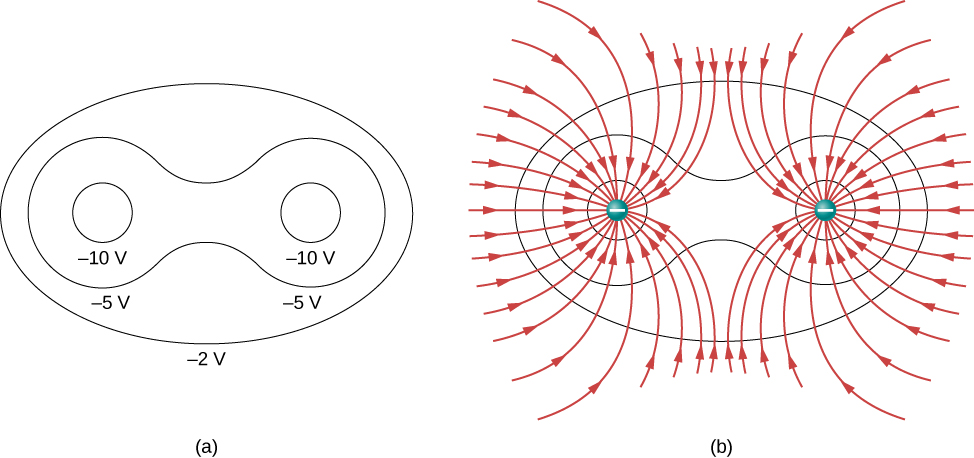
Umgekehrt können bei gegebenen Äquipotentiallinien, wie in Abbildung \(\PageIndex{2a}\), die elektrischen Feldlinien gezeichnet werden, indem man sie senkrecht zu den Äquipotentialen macht, wie in Abbildung \(\PageIndex{2b}\).
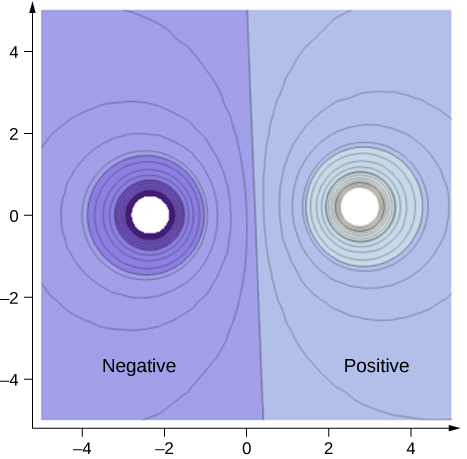
Zur Verbesserung Ihrer Intuition zeigen wir eine dreidimensionale Variante des Potentials in einem System mit zwei entgegengesetzten Ladungen. Die Abbildung zeigt eine dreidimensionale Karte des elektrischen Potentials, wobei die Linien auf der Karte für Äquipotentialflächen stehen, wobei der Berg bei der positiven Ladung und die Senke bei der negativen Ladung liegt. Beachten Sie, dass der Schnitt bei einem bestimmten Potential impliziert, dass sich die Ladungen auf leitenden Kugeln mit einem endlichen Radius befinden.
Abbildung (\PageIndex{4}\): Abbildung des elektrischen Potenzials zweier gleich großer, entgegengesetzter Ladungen auf leitenden Kugeln. Das Potenzial ist in der Nähe der negativen Ladung negativ und in der Nähe der positiven Ladung positiv. Dieses dynamische Bild wird von CalcPlot3D unterstützt und kann hier betrachtet werden.
Eine zweidimensionale Karte der Querschnittsebene, die beide Ladungen enthält, ist in Abbildung \(\PageIndex{5}\) dargestellt. Die Linie, die von den beiden entgegengesetzten Ladungen äquidistant ist, entspricht dem Nullpotential, da an den Punkten auf der Linie das positive Potential der positiven Ladung das negative Potential der negativen Ladung aufhebt. Äquipotentiallinien in der Querschnittsebene sind geschlossene Schleifen, die nicht notwendigerweise Kreise sind, da an jedem Punkt das Nettopotential die Summe der Potentiale von jeder Ladung ist.
Hinweis
In dieser Simulation können Sie die Äquipotentialflächen und elektrischen Felder für viele Standard-Ladungskonfigurationen beobachten und verändern. Es gibt eine Menge zu erforschen.
Einer der wichtigsten Fälle ist der der bekannten parallelleitenden Platten in Abbildung \(\PageIndex{6}\). Zwischen den Platten liegen die Äquipotentiale in gleichem Abstand und parallel. Das gleiche Feld könnte erhalten werden, indem man leitende Platten an den Äquipotentiallinien bei den gezeigten Potentialen anordnet.
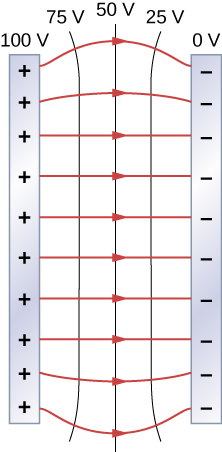
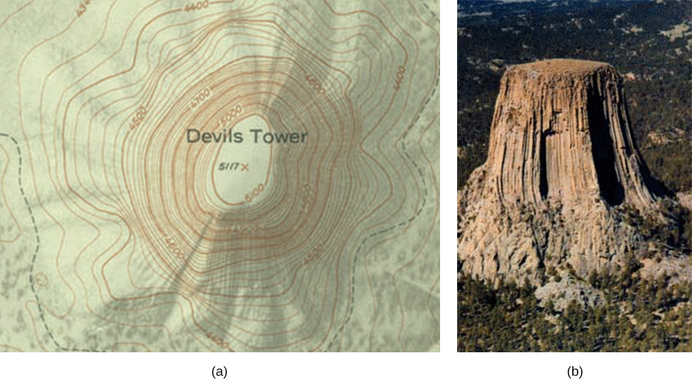
Betrachten Sie die parallelen Platten Abbildung \(\PageIndex{6}\). Diese haben Äquipotentiallinien, die parallel zu den Platten im Zwischenraum liegen und gleichmäßig beabstandet sind. Ein Beispiel hierfür (mit Beispielwerten) ist in Abbildung \(\PageIndex{6}\) dargestellt. Wir könnten einen ähnlichen Satz von Äquipotential-Isolinien für die Schwerkraft auf Hügeln zeichnen. Wenn der Hügel eine beliebige Ausdehnung am gleichen Hang hat, würden die Isolinien entlang dieser Ausdehnung parallel zueinander verlaufen. Außerdem würden die Isolinien in Regionen mit konstanter Neigung gleichmäßig verteilt sein. Ein Beispiel für reale topographische Linien ist in Abbildung \(\PageIndex{7}\) dargestellt.
Beispiel: Berechnen vonÄquipotentiallinien
Die Äquipotentiallinien einer Punktladung haben Sie inAbbildung \(\PageIndex{1}\) gesehen. Wie können wir sie berechnen? Wenn wir zum Beispiel eine \(+10-nC\)-Ladung im Ursprung haben, wie lauten die Äquipotentialflächen, an denen das Potential (a) 100 V, (b) 50 V, (c) 20 V und (d) 10 V beträgt?
Strategie
Setzen Sie die Gleichung für das Potential einer Punktladung gleich einer Konstante und lösen Sie für die verbleibende(n) Variable(n). Berechnen Sie dann die Werte nach Bedarf.
Lösung
In \(V = k\dfrac{q}{r}\) sei V eine Konstante. Die einzige verbleibende Variable ist r; daher ist \(r = k\dfrac{q}{V} =konstant\). Die Äquipotentialflächen sind also Kugeln um den Ursprung. Ihre Positionen sind:
- \(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{100 \, V} = 0,90 \, m\);
- \(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{50 \, V} = 1.8 \, m\);
- \(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{20 \, V} = 4.5 \, m\);
- \(r = k\dfrac{q}{V} = \left(8,99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{10 \, V} = 9,0 \, m\).
Bedeutung
Das bedeutet, dass Äquipotentialflächen um eine Punktladung, wie oben gezeigt, Kugeln mit konstantem Radius und wohldefinierter Lage sind.
Beispiel \(\PageIndex{2}\): Potentialdifferenz zwischen entgegengesetzt geladenen parallelen Platten
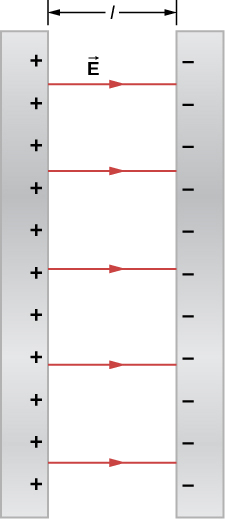
Zwei große leitende Platten tragen gleiche und entgegengesetzte Ladungen, mit einer Oberflächenladungsdichte \(\Sigma\) der Größenordnung \(6,81 \mal10^{-7} C/m\), wie in Abbildung \(\PageIndex{8}\) gezeigt. Der Abstand zwischen den Platten ist \(l = 6,50 \, mm\).
- Wie groß ist das elektrische Feld zwischen den Platten?
- Wie groß ist die Potentialdifferenz zwischen den Platten?
- Wie groß ist der Abstand zwischen Äquipotentialflächen, die sich um 100 V unterscheiden?
Strategie
- Da die Platten als „groß“ beschrieben werden und der Abstand zwischen ihnen nicht, werden wir jede von ihnen als eine unendliche Ebene annähern und das Ergebnis aus dem Gaußschen Gesetz im vorigen Kapitel anwenden.
- Verwenden Sie \(\Delta V_{AB} = – \int_A^B \vec{E} \cdot d\vec{l}\).
- Da das elektrische Feld konstant ist, finden Sie das Verhältnis von 100 V zur gesamten Potentialdifferenz; dann berechnen Sie diesen Bruchteil der Entfernung.
Lösung
a. Das elektrische Feld ist von der positiven zur negativen Platte gerichtet, wie in der Abbildung gezeigt, und sein Betrag ist gegeben durch
&= \dfrac{6.81 \times 10^{-7} C/m^2}{8,85 \Times 10^{-12} C^2/N\cdot m^2} \\ &= 7,69 \Times 10^4 \, V/m. \end{align*}\]
b. Um die Potentialdifferenz \(\Delta V\) zwischen den Platten zu finden, verwenden wir einen Weg von der negativen zur positiven Platte, der gegen das Feld gerichtet ist. Der Verschiebungsvektor \(d\vec{l}\) und das elektrische Feld \(\vec{E}\) sind antiparallel, so dass \(\vec{E}\cdot d\vec{l} = – E \, dl\). Die Potentialdifferenz zwischen der positiven Platte und der negativen Platte ist dann
&= E \int dl \\ &= El \\ &= (7.69 \times 10^4V/m)(6.50 \times 10^{-3}m) \\\ &= 500 \, V \end{align*}\]
c. Die gesamte Potenzialdifferenz beträgt 500 V, also ist 1/5 des Abstands zwischen den Platten der Abstand zwischen 100-V-Potenzialdifferenzen. Der Abstand zwischen den Platten beträgt 6,5 mm, so dass der Abstand zwischen 100-V-Potentialdifferenzen 1,3 mm beträgt.
Bedeutung
Sie haben nun eine numerische Berechnung der Orte der Potentiale zwischen zwei geladenen parallelen Platten gesehen.
Wie lauten die Äquipotentialflächen für eine unendliche Linienladung?
Antwort
unendliche Zylinder mit konstantem Radius, mit der Linienladung als Achse
Ladungsverteilung auf Leitern
In Beispiel \(\PageIndex{1}\) mit einer Punktladung haben wir festgestellt, dass die Äquipotentialflächen die Form von Kugeln haben, mit der Punktladung im Zentrum. Da eine leitende Kugel im elektrostatischen Gleichgewicht eine kugelförmige Äquipotentialfläche ist, sollten wir erwarten, dass wir eine der Flächen in Beispiel \(\PageIndex{2}\) durch eine leitende Kugel ersetzen können und eine identische Lösung außerhalb der Kugel erhalten. Im Inneren wird es jedoch ganz anders aussehen.
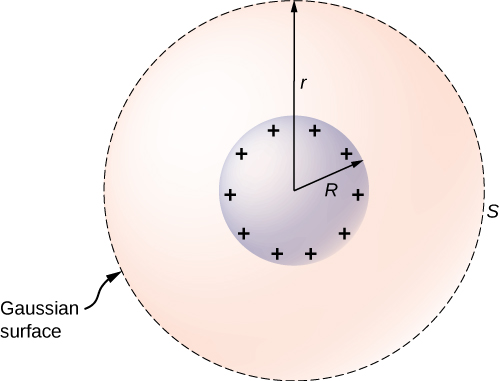
Um dies zu untersuchen, betrachten wir die isolierte leitende Kugel ausAbbildung \(\PageIndex{9}\), die einen Radius R und eine Überladung q hat. Um das elektrische Feld sowohl innerhalb als auch außerhalb der Kugel zu finden, beachten wir, dass die Kugel isoliert ist, so dass ihre Oberflächenänderungsverteilung und das elektrische Feld dieser Verteilung sphärisch symmetrisch sind. Wir können daher das Feld als \(\vec{E} = E(r)\hat{r}\) darstellen. Um \(E(r)\) zu berechnen, wenden wir das Gaußsche Gesetz auf eine geschlossene Kugeloberfläche S mit dem Radius r an, die konzentrisch zur leitenden Kugel ist. Da \(r\) konstant ist und \(\hat{n} = \hat{r}\) auf der Sphäre,
&=E(r) 4\pi r^2. \end{align}\]
Für \(r < R\) liegt \(S\) innerhalb des Leiters, also erinnern wir uns aus unserer vorherigen Untersuchung des Gaußschen Gesetzes daran, dass \(q_{enc} = 0\) und das Gaußsche Gesetz \(E(r) = 0\) ergibt, wie es innerhalb eines Leiters im Gleichgewicht erwartet wird. Wenn \(r > R\), S den Leiter umschließt, so\(q_{enc} = q\). Aus dem Gauß’schen Gesetz,
Das elektrische Feld der Kugel kann also geschrieben werden als
und
Wie erwartet, ist im Bereich \(r \geq R\) das elektrische Feld einer Ladung q auf einer isolierten leitenden Kugel mit dem Radius R identisch mit dem elektrischen Feld einer Punktladung q, die sich im Zentrum der Kugel befindet.
Um das elektrische Potential innerhalb und außerhalb der Kugel zu finden, beachten Sie, dass für \(r \geq R\) das Potential dasselbe sein muss wie das einer isolierten Punktladung q, die sich bei \(r = 0\) befindet,
einfach aufgrund der Ähnlichkeit des elektrischen Feldes.
Für \(r < R, \, E = 0\), ist also V(r) in diesem Bereich konstant. Da \(V(R) = q/4\pi \epsilon_0 R\),
Wir werden dieses Ergebnis verwenden, um zu zeigen, dass
für zwei leitende Kugeln der Radien \(R_1\) und \(R_2\), mit Oberflächenladungsdichten \(\sigma_1\) bzw. \(\sigma_2\), die durch einen dünnen Draht verbunden sind, wie in Abbildung\(\PageIndex{10}\) gezeigt. Die Kugeln sind ausreichend voneinander getrennt, so dass jede so behandelt werden kann, als wäre sie isoliert (abgesehen von dem Draht).

Wir haben soeben gesehen, dass das elektrische Potential an der Oberfläche einer isolierten, geladenen leitenden Kugel mit dem Radius Ris
Nun sind die Kugeln durch einen Leiter verbunden und haben somit das gleiche Potential; daher
und
Die Nettoladung auf einer leitenden Kugel und ihre Oberflächenladungsdichte sind durch \(q = \sigma (4\pi R^2)\) verbunden. Setzt man diese Gleichung in die vorhergehende ein, erhält man
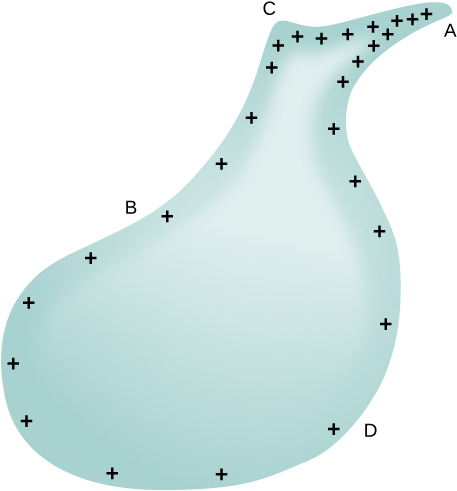
Obwohl zwei Kugeln, die durch einen dünnen Draht verbunden sind, keinen typischen Leiter mit variablem Krümmungsradius darstellen, liefert dieses Ergebnis zumindest eine qualitative Vorstellung davon, wie die Ladungsdichte über die Oberfläche eines Leiters variiert. Die Gleichung zeigt, dass dort, wo der Krümmungsradius groß ist (Punkte B und D in \(\PageIndex{11}\)), \(\Sigma\) und E klein sind.
Analog dazu sind die Ladungen tendenziell dichter, wo die Krümmung der Oberfläche größer ist, wie die Ladungsverteilung auf ungerade geformtem Metall (Abbildung \(\PageIndex{11}\)) zeigt. Die Oberflächenladungsdichte ist an Stellen mit einem kleinen Krümmungsradius höher als an Stellen mit einem großen Krümmungsradius.
Eine praktische Anwendung dieses Phänomens ist der Blitzableiter, der einfach ein geerdeter Metallstab mit einem spitzen Ende ist, das nach oben zeigt. Da sich durch eine negativ geladene Wolke über dem Boden positive Ladung ansammelt, wird das elektrische Feld um die Spitze sehr groß. Wenn das Feld einen Wert von etwa \(3,0 \mal 10^6 N/C\) (die Durchschlagsfestigkeit der Luft) erreicht, werden die freien Ionen in der Luft auf so hohe Energien beschleunigt, dass ihre Kollisionen mit Luftmolekülen die Moleküle tatsächlich ionisieren. Die entstehenden freien Elektronen in der Luft fließen dann durch den Stab zur Erde und neutralisieren so einen Teil der positiven Ladung. Dadurch wird verhindert, dass das elektrische Feld zwischen der Wolke und der Erde groß genug wird, um einen Blitz in der Region um den Stab zu erzeugen.
Eine wichtige Anwendung von elektrischen Feldern und Äquipotentiallinien betrifft das Herz. Das Herz ist auf elektrische Signale angewiesen, um seinen Rhythmus aufrechtzuerhalten. Die Bewegung der elektrischen Signale bewirkt, dass sich die Kammern des Herzens zusammenziehen und entspannen. Wenn eine Person einen Herzinfarkt hat, kann die Bewegung dieser elektrischen Signale gestört sein. Ein künstlicher Herzschrittmacher und ein Defibrillator können verwendet werden, um den Rhythmus der elektrischen Signale zu initiieren. Die Äquipotentiallinien um das Herz, die Thoraxregion und die Herzachse sind nützliche Mittel, um die Struktur und die Funktionen des Herzens zu überwachen. Ein Elektrokardiogramm (EKG) misst die kleinen elektrischen Signale, die während der Aktivität des Herzens entstehen.
PheT
Spielen Sie mit dieser Simulation, um Punktladungen auf dem Spielfeld zu bewegen und dann das elektrische Feld, Spannungen, Äquipotentiallinien und mehr zu betrachten.
Mitwirkende und Namensnennung
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) und Bill Moebs mit vielen mitwirkenden Autoren. Dieses Werk ist lizenziert von OpenStax University Physics unter einer Creative Commons Attribution License (by 4.0).