Die Cramersche Regel ist eine weitere Methode, die lineare Gleichungssysteme mit Hilfe von Determinanten lösen kann.
In Bezug auf die Notation ist eine Matrix eine Reihe von Zahlen, die von eckigen Klammern umschlossen sind, während die Determinante eine Reihe von Zahlen ist, die von zwei senkrechten Balken umschlossen sind.
Notationen
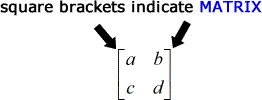
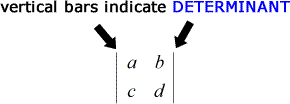
Die Formel zum Finden der Determinante einer 2 x 2 Matrix ist sehr einfach.
Lassen Sie uns einen kurzen Blick darauf werfen:
Die Determinante einer 2 x 2 Matrix
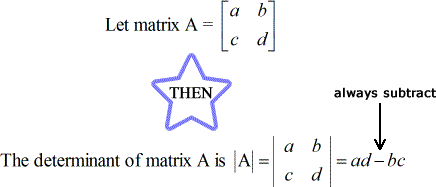
Schnelle Beispiele, wie man die Determinanten einer 2 x 2 Matrix findet
Beispiel 1: Finden Sie die Determinante der folgenden Matrix A.
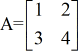
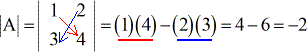
Beispiel 2: Finden Sie die Determinante der folgenden Matrix B.
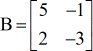
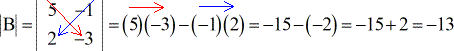
Beispiel 3: Finden Sie die Determinante der folgenden Matrix C.
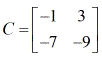
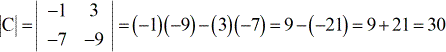
Nachdem Sie wissen, wie man die Determinante einer 2 x 2 Matrix findet, sind Sie nun bereit, die Prozeduren oder Schritte zu lernen, wie man die Cramersche Regel verwendet. Los geht’s!
Cramersche Regeln für lineare Gleichungssysteme mit zwei Variablen
- Gegeben ein lineares System

- Vergeben Sie Namen für jede Matrix
Koeffizientenmatrix:
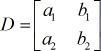
X – Matrix:
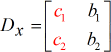
Y – Matrix:
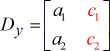
Um die Variable x zu lösen.
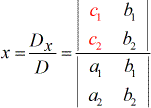
Um die Variable y zu lösen.
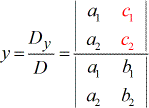
Einige Punkte, die bei der Betrachtung der Formel zu beachten sind:
1) Die Spalten von \large{x}, \large{y} und die konstanten Terme \large{c} ergeben sich wie folgt:
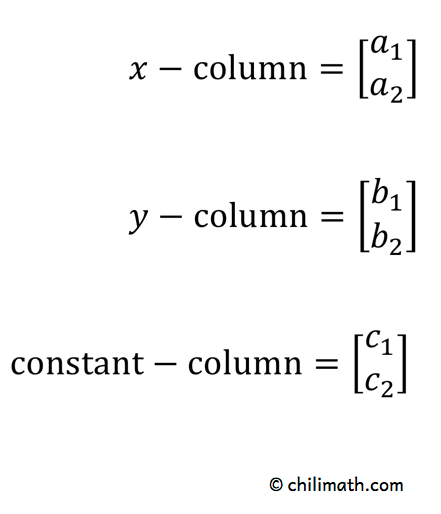
2) Die beiden Nenner beim Lösen von \large{x} und \large{y} sind gleich. Sie stammen aus den Spalten von \large{x} und \large{y}.
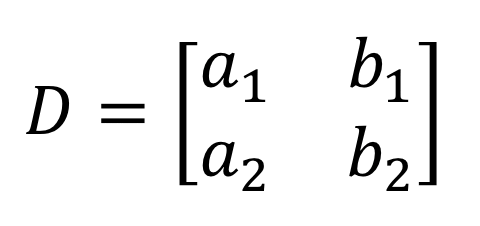
3) Betrachtet man den Zähler beim Lösen von \large{x}, so werden die Koeffizienten der \large{x}-Spalte durch die Konstanten-Spalte (in rot) ersetzt.
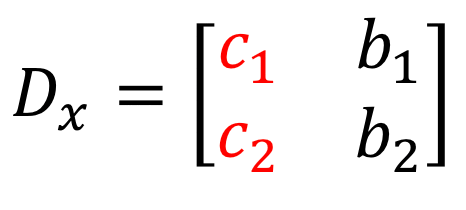
4) Auf die gleiche Weise werden beim Lösen für \large{y} die Koeffizienten der \large{y}-Spalte durch die konstante Spalte (in rot) ersetzt.
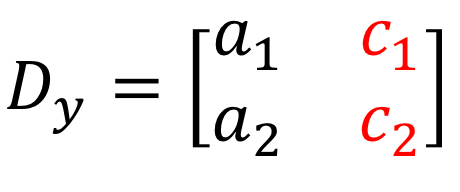
Beispiele, wie man Lösen von Systemen linearer Gleichungen mit zwei Variablen mit Hilfe der Cramerschen Regel
Beispiel 1: Lösen Sie das System mit zwei Variablen mit Hilfe der Cramerschen Regel
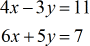
Beginnen Sie mit dem Extrahieren der drei relevanten Matrizen: Koeffizient, \large{x}, und \large{y}. Lösen Sie dann die entsprechenden Determinanten.
- Für die Koeffizientenmatrix
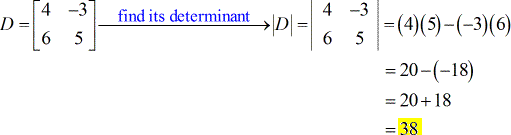
- Für X – Matrix

- Für die Y-Matrix

Sobald alle drei Determinanten berechnet sind, ist es an der Zeit, die Werte von \large{x} und \large{y} mithilfe der obigen Formel zu lösen.
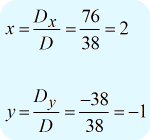
Ich kann die endgültige Antwort als \large{\left( {x,y} \right) = \left( {2, – 1} \right)} schreiben.
Beispiel 2: Lösen Sie das System mit zwei Variablen nach der Cramerschen Regel
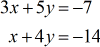
Bestimmen Sie die Koeffizienten-, \large{x}- und \large{y}-Matrizen aus dem gegebenen System linearer Gleichungen. Berechnen Sie dann deren Determinanten entsprechend.
Erinnern Sie sich, dass wir immer die Produkte der Diagonaleinträge subtrahieren.
- Für die Koeffizientenmatrix (verwenden Sie die Koeffizienten der beiden Variablen x und y)
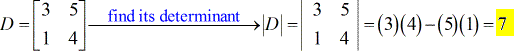
- Für die X – Matrix (ersetzen Sie die x-Spalte durch die Konstanten-Spalte)
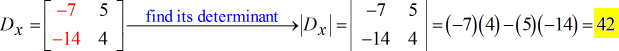
- Für die Y – Matrix (ersetzen Sie die y-Spalte durch die Konstanten-Spalte)
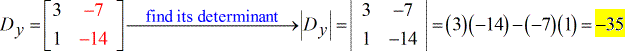
Ich hoffe, Sie fühlen sich langsam wohl beim Rechnen für die Determinante einer 2-dimensionalen Matrix. Um schließlich die benötigten Variablen zu lösen, erhalte ich folgende Ergebnisse…
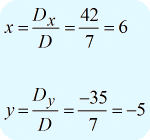
Schreibt man die endgültige Antwort in Punktschreibweise, erhält man \large{\left( {x,y} \right) = \left( {6, – 5} \right)}.
Beispiel 3: Lösen Sie das System mit zwei Variablen mit der Cramerschen Regel
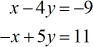
Dieses Problem lässt sich eigentlich recht einfach mit der Eliminationsmethode lösen. Das liegt daran, dass die Koeffizienten der Variablen x „gleich“ sind, aber nur entgegengesetzte Vorzeichen haben ( +1 und -1 ). Um dies mit der Eliminationsmethode zu lösen, addieren Sie die entsprechenden Spalten und die x-Variable verschwindet – übrig bleibt eine Einschrittgleichung in \large{y}. Ich erwähne dies, weil jede Technik ihre Schwächen hat und es am besten ist, die effizienteste zu wählen. Klären Sie immer mit Ihrem Lehrer, ob es in Ordnung ist, einen anderen Ansatz zu verwenden, wenn die Methode für ein bestimmtes Problem nicht angegeben ist.
Also, da wir lernen, wie man nach der Cramerschen Regel löst, lassen Sie uns mit dieser Methode weitermachen.
Ich werde drei Matrizen (Koeffizient, \large{x} und \large{y}) konstruieren und ihre entsprechenden Determinanten auswerten.
- Für die Koeffizientenmatrix
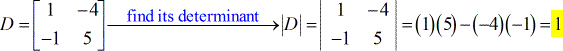
- Für die X – Matrix ( geschrieben als großes D mit tiefgestelltem x )
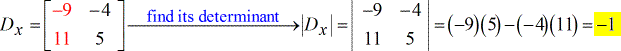
- Für die Y-Matrix (geschrieben als großes D mit tiefgestelltem y)
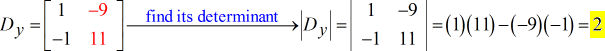
Nachdem ich die Werte der drei benötigten Determinanten erhalten habe, werde ich \large{x} und \large{y} wie folgt berechnen.
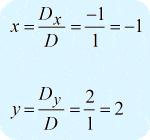
Die endgültige Antwort in der Punktform ist \large{\left( {x,y} \right) = \left( { – 1,2} \right)} .
Beispiel 4: Lösen Sie mit Hilfe der Cramerschen Regel das System mit zwei Variablen
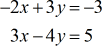
Da wir schon ein paar Beispiele durchgegangen sind, schlage ich vor, dass Sie diese Aufgabe selbst versuchen. Vergleichen Sie dann Ihre Antworten mit der Lösung unten.
Wenn Sie es beim ersten Mal richtig machen, bedeutet das, dass Sie ein „Profi“ in Bezug auf die Cramer’sche Regel werden. Wenn nicht, versuchen Sie herauszufinden, was falsch gelaufen ist und lernen Sie, den gleichen Fehler beim nächsten Mal nicht mehr zu begehen. So werden Sie besser in Mathe. Studieren Sie viele Arten von Problemen und, was noch wichtiger ist, machen Sie eine Menge unabhängiger Übungen.
- Für die Koeffizientenmatrix
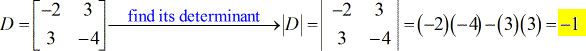
- Für die x-Matrix
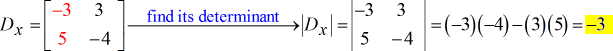
- Für die Y-Matrix
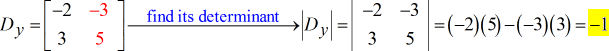
Sie sollten die Antwort unten erhalten…
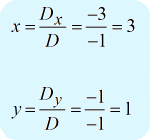
Beispiel 5: Lösen Sie das System mit zwei Variablen mit der Cramerschen Regel
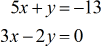
Für unser letztes Beispiel habe ich eine Null in die Konstanten-Spalte gesetzt. Jedes Mal, wenn Sie die Zahl Null in der Konstanten-Spalte sehen, empfehle ich dringend, die Cramersche Regel zu verwenden, um das lineare Gleichungssystem zu lösen. Warum? Weil die Berechnung der Determinanten für \large{x} und \large{y} Matrizen drastisch vereinfacht wird. Probieren Sie es selbst aus!
- Für die Koeffizientenmatrix
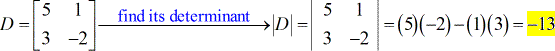
- Für X – Matrix
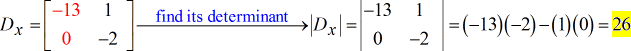
- Für die Y – Matrix
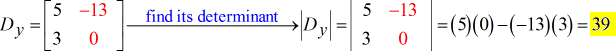
Die endgültige Lösung dieser Aufgabe ist
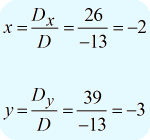
Üben mit Arbeitsblättern
Sie interessieren sich vielleicht auch für:
Cramersche Regel 3×3