Sampling ist definiert als, „Der Prozess der Messung der Momentanwerte eines zeitkontinuierlichen Signals in einer diskreten Form.“
Sample ist ein Teil der Daten, der aus den gesamten Daten, die im Zeitbereich kontinuierlich sind, entnommen wird.
Wenn eine Quelle ein analoges Signal erzeugt und dieses digitalisiert werden soll, das 1s und 0s hat, d.h., High oder Low, muss das Signal zeitlich diskretisiert werden. Diese Diskretisierung des analogen Signals wird als Sampling bezeichnet.
Die folgende Abbildung zeigt ein zeitkontinuierliches Signal x (t) und ein gesampeltes Signal xs (t). Wenn x (t) mit einer periodischen Impulsfolge multipliziert wird, erhält man das abgetastete Signal xs (t).
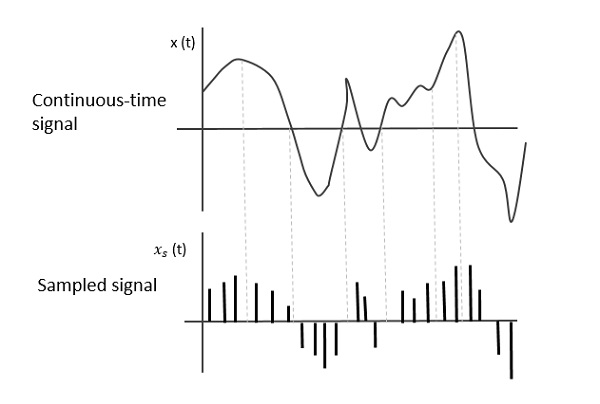
Abtastrate
Um die Signale zu diskretisieren, sollte der Abstand zwischen den Abtastungen festgelegt werden. Diese Lücke kann als Abtastperiode Ts bezeichnet werden.
$Abtastung \: Frequenz = \frac{1}{T_{s}} = f_s$
Wobei,
-
$T_{s}$ die Abtastzeit ist
-
$f_{s}$ die Abtastfrequenz oder die Abtastrate ist
Die Abtastfrequenz ist der Kehrwert der Abtastperiode. Diese Abtastfrequenz, kann einfach als Abtastrate bezeichnet werden. Die Abtastrate bezeichnet die Anzahl der Abtastungen pro Sekunde oder für eine endliche Menge von Werten.
Damit ein analoges Signal aus dem digitalisierten Signal rekonstruiert werden kann, sollte die Abtastrate gut überlegt sein. Die Abtastrate sollte so gewählt werden, dass die Daten im Nachrichtensignal weder verloren gehen noch überlagert werden. Daher wurde dafür eine Rate festgelegt, die als Nyquist-Rate bezeichnet wird.
Nyquist-Rate
Angenommen, ein Signal ist bandbegrenzt und hat keine Frequenzkomponenten, die höher als W Hertz sind. Das heißt, W ist die höchste Frequenz. Für ein solches Signal sollte die Abtastrate für eine effektive Reproduktion des Originalsignals das Doppelte der höchsten Frequenz betragen.
Das bedeutet,
$f_{S} = 2W$
Wobei,
-
$f_{S}$ die Abtastrate ist
-
W ist die höchste Frequenz
Diese Abtastrate wird als Nyquist-Rate bezeichnet.
Zur Theorie dieser Nyquist-Rate wurde ein Theorem aufgestellt, das Sampling-Theorem.
Sampling-Theorem
Das Sampling-Theorem, das auch als Nyquist-Theorem bezeichnet wird, liefert die Theorie der ausreichenden Abtastrate in Bezug auf die Bandbreite für die Klasse der Funktionen, die bandbegrenzt sind.
Das Abtasttheorem besagt, dass „ein Signal exakt reproduziert werden kann, wenn es mit der Rate fs abgetastet wird, die größer als das Doppelte der maximalen Frequenz W ist.“
Um dieses Abtasttheorem zu verstehen, betrachten wir ein bandbegrenztes Signal, d.h., ein Signal, dessen Wert zwischen einigen -W und W Hertz nicht Null ist.
Ein solches Signal wird dargestellt als $x(f) = 0 für |f\lvert > W$
Für das zeitkontinuierliche Signal x (t) kann das bandbegrenzte Signal im Frequenzbereich wie in der folgenden Abbildung dargestellt werden.
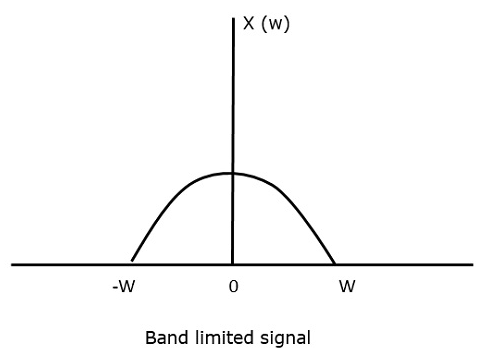
Wir benötigen eine Abtastfrequenz, eine Frequenz, bei der auch nach der Abtastung kein Informationsverlust auftreten darf. Dafür gibt es die Nyquist-Rate, die besagt, dass die Abtastfrequenz das Zweifache der Maximalfrequenz betragen sollte. Sie ist die kritische Abtastrate.
Wird das Signal x(t) oberhalb der Nyquist-Rate abgetastet, kann das ursprüngliche Signal wiederhergestellt werden, wird es unterhalb der Nyquist-Rate abgetastet, kann das Signal nicht wiederhergestellt werden.
Die folgende Abbildung erklärt ein Signal, wenn es mit einer höheren Rate als 2w im Frequenzbereich abgetastet wird.
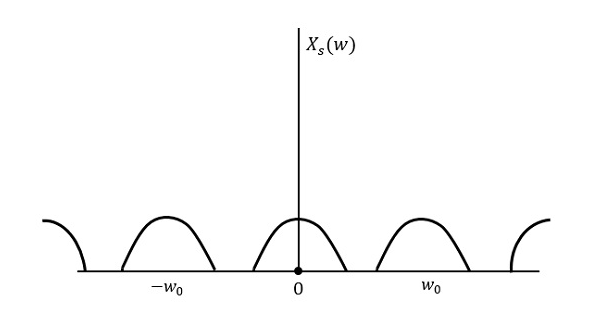
Die obige Abbildung zeigt die Fouriertransformation eines Signals $x_{s}(t)$. Hier wird die Information ohne Verlust wiedergegeben. Es gibt keine Verwechslung und somit ist eine Wiederherstellung möglich.
Die Fourier-Transformation des Signals $x_{s}(t)$ ist
$X_{s}(w) = \frac{1}{T_{s}}\sum_{n = – \infty}^\infty X(w-nw_0)$
Wobei $T_{s}$ = Abtastperiode und $w_{0} = \frac{2 \pi}{T_s}$
Lassen Sie uns sehen, was passiert, wenn die Abtastrate gleich dem Doppelten der höchsten Frequenz ist (2W)
Das bedeutet,
$f_{s} = 2W$
Wobei,
-
$f_{s}$ ist die Abtastfrequenz
-
W ist die höchste Frequenz
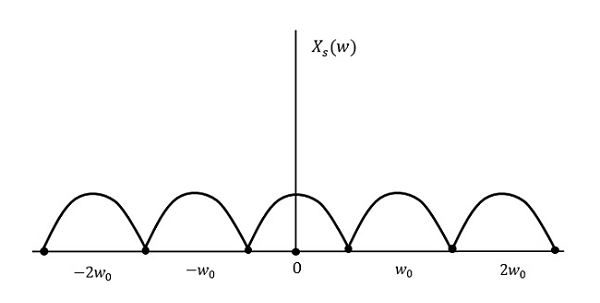
Das Ergebnis ist wie in der obigen Abbildung dargestellt. Die Information wird ohne Verlust ersetzt. Daher ist dies auch eine gute Abtastrate.
Betrachten wir nun die Bedingung,
$f_{s} Das resultierende Muster sieht wie in der folgenden Abbildung aus.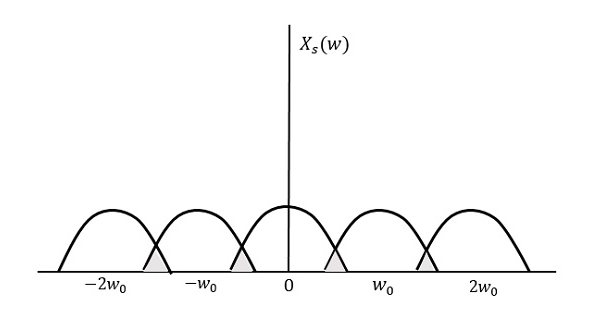
Aus dem obigen Muster können wir erkennen, dass eine Überlappung der Informationen stattfindet, was zu einer Vermischung und einem Verlust von Informationen führt. Dieses unerwünschte Phänomen der Überlappung wird als Aliasing bezeichnet.
Aliasing
Aliasing kann als „das Phänomen einer hochfrequenten Komponente im Spektrum eines Signals, die die Identität einer niederfrequenten Komponente im Spektrum seiner abgetasteten Version annimmt“ bezeichnet werden.“
Die Korrekturmaßnahmen zur Verringerung des Aliasing-Effekts sind –
-
Im Sendeteil von PCM wird vor dem Sampler ein Tiefpass-Anti-Aliasing-Filter eingesetzt, um die unerwünschten Hochfrequenzanteile zu eliminieren.
-
Das Signal, das nach der Filterung abgetastet wird, wird mit einer Rate abgetastet, die etwas höher ist als die Nyquist-Rate.
Diese Wahl einer höheren Abtastrate als die Nyquist-Rate hilft auch bei der einfacheren Gestaltung des Rekonstruktionsfilters am Empfänger.
Umfang der Fourier-Transformation
Es wird allgemein beobachtet, dass wir die Hilfe von Fourier-Reihen und Fourier-Transformationen bei der Analyse der Signale und auch beim Beweisen von Theoremen suchen. Das liegt daran, dass –
-
Die Fourier-Transformation ist die Erweiterung der Fourier-Reihe für nicht-periodische Signale.
-
Die Fourier-Transformation ist ein leistungsfähiges mathematisches Werkzeug, das hilft, die Signale in verschiedenen Bereichen zu betrachten und die Signale leicht zu analysieren.
-
Mit Hilfe der Fourier-Transformation kann jedes Signal in die Summe von Sinus und Kosinus zerlegt werden.
Im nächsten Kapitel wollen wir das Konzept der Quantisierung besprechen.