Probit-Regression
In der Probit-Regression, wird die kumulative Standardnormalverteilungsfunktion \(\Phi(\cdot)\) verwendet, um die Regressionsfunktion zu modellieren, wenn die abhängige Variable binär ist, das heißt, wir nehmen an, dass\
(\beta_0 + \beta_1 X\) in (11.4) die Rolle eines Quantils \(z\) an. Denken Sie daran, dass \ so ist, dass der Probit-Koeffizient \(\beta_1\) in (11.4) die Änderung von \(z\) ist, die mit einer Änderung von \(X\) um eine Einheit verbunden ist. Obwohl die Auswirkung einer Änderung von \(X\) auf \(z\) linear ist, ist der Zusammenhang zwischen \(z\) und der abhängigen Variable \(Y\) nichtlinear, da \(\Phi\) eine nichtlineare Funktion von \(X\) ist.
Da die abhängige Variable eine nichtlineare Funktion der Regressoren ist, hat der Koeffizient für \(X\) keine einfache Interpretation. Gemäß Schlüsselkonzept 8.1 kann die erwartete Änderung der Wahrscheinlichkeit, dass \(Y=1\) aufgrund einer Änderung von \(P/I \\) wie folgt berechnet werden:
- Berechnen Sie die vorhergesagte Wahrscheinlichkeit, dass \(Y=1\) für den ursprünglichen Wert von \(X\).
- Berechnen Sie die vorhergesagte Wahrscheinlichkeit, dass \(Y=1\) für \(X + \Delta X\).
- Berechnen Sie die Differenz zwischen beiden vorhergesagten Wahrscheinlichkeiten.
Natürlich können wir (11.4) auf die Probit-Regression mit mehreren Regressoren verallgemeinern, um das Risiko der Verzerrung durch ausgelassene Variablen zu verringern. Die Grundlagen der Probit-Regression sind in Schlüsselkonzept 11.2 zusammengefasst.
Probit-Modell, vorhergesagte Wahrscheinlichkeiten und geschätzte Effekte
Angenommen, \(Y\) ist eine binäre Variable. Das Modell
ist das Populations-Probit-Modell mit mehreren Regressoren \(X_1, X_2, \dots, X_k\) und \(\Phi(\cdot)\) ist die kumulative Standardnormalverteilungsfunktion.
Die Vorhersagewahrscheinlichkeit, dass \(Y=1\) bei \(X_1, X_2, \dots, X_k\) gegeben ist, kann in zwei Schritten berechnet werden:
-
Berechnen Sie \(z = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k\)
-
Ermitteln Sie \(\Phi(z)\) durch Aufruf von pnorm().
(\beta_j\) ist der Effekt auf \(z\) einer Änderung des Regressors \(X_j\) um eine Einheit, wobei alle anderen \(k-1\) Regressoren konstant gehalten werden.
Der Effekt auf die vorhergesagte Wahrscheinlichkeit einer Änderung in einem Regressor kann wie in Schlüsselkonzept 8.1 berechnet werden.
In R können Probit-Modelle mit der Funktion glm() aus dem Paket stats geschätzt werden. Mit dem Argument family geben wir an, dass wir eine Probit-Verknüpfungsfunktion verwenden wollen.
Wir schätzen nun ein einfaches Probit-Modell der Wahrscheinlichkeit einer Hypothekenverweigerung.
# estimate the simple probit modeldenyprobit <- glm(deny ~ pirat, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Das geschätzte Modell ist
Gleich wie im linearen Wahrscheinlichkeitsmodell finden wir, dass der Zusammenhang zwischen der Ablehnungswahrscheinlichkeit und dem Verhältnis von Zahlungen zu Einkommen positiv ist und dass der entsprechende Koeffizient hoch signifikant ist.
Der folgende Codeschnipsel reproduziert Abbildung 11.2 des Buches.
# plot dataplot(x = HMDA$pirat, y = HMDA$deny, main = "Probit Model of the Probability of Denial, Given P/I Ratio", xlab = "P/I ratio", ylab = "Deny", pch = 20, ylim = c(-0.4, 1.4), cex.main = 0.85)# add horizontal dashed lines and textabline(h = 1, lty = 2, col = "darkred")abline(h = 0, lty = 2, col = "darkred")text(2.5, 0.9, cex = 0.8, "Mortgage denied")text(2.5, -0.1, cex= 0.8, "Mortgage approved")# add estimated regression linex <- seq(0, 3, 0.01)y <- predict(denyprobit, list(pirat = x), type = "response")lines(x, y, lwd = 1.5, col = "steelblue")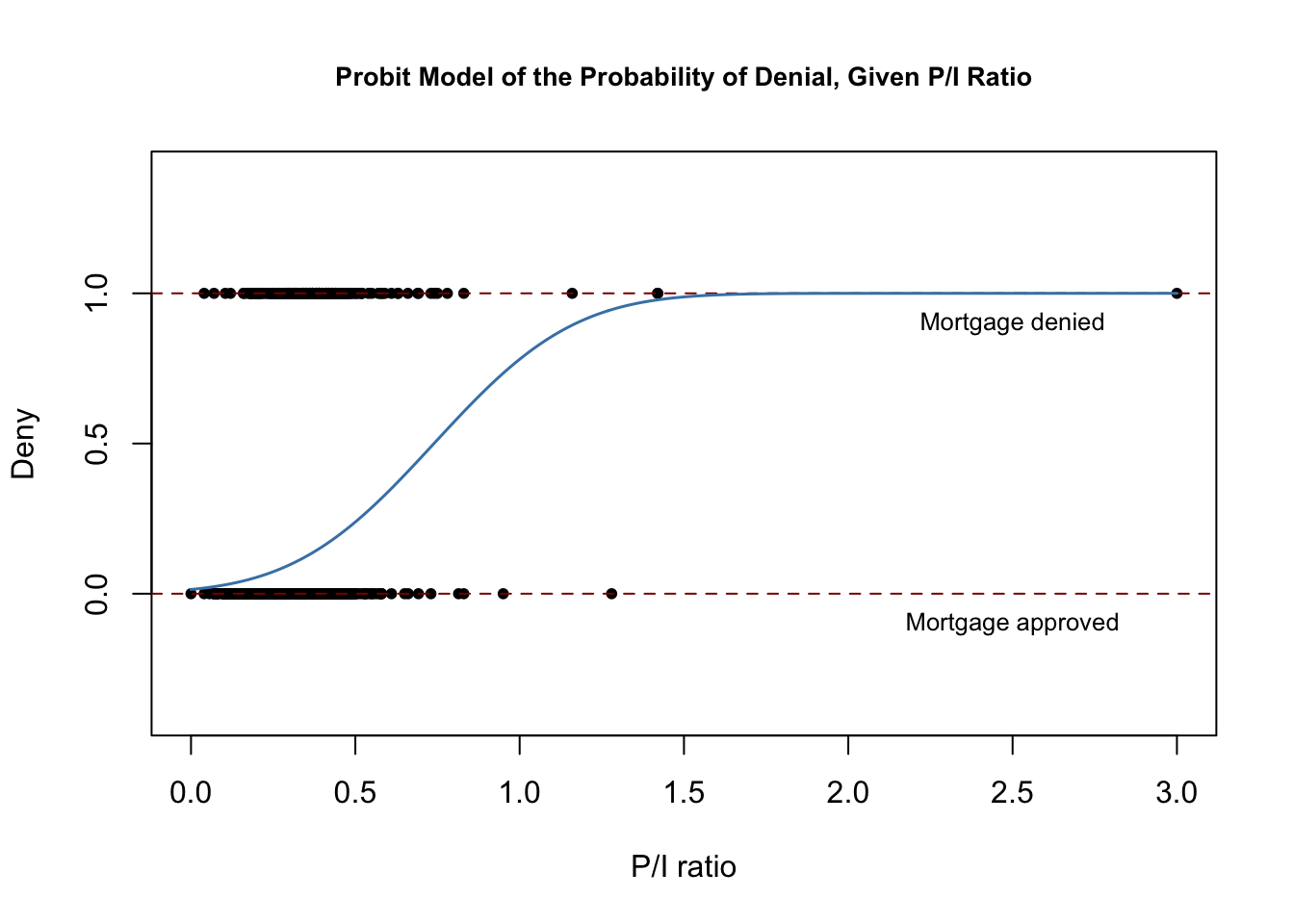
Die geschätzte Regressionsfunktion hat eine gestreckte „S“-Form, die typisch für die CDF einer kontinuierlichen Zufallsvariablen mit symmetrischer PDF wie der einer normalen Zufallsvariablen ist. Die Funktion ist eindeutig nichtlinear und flacht für große und kleine Werte von \(P/I \ ratio\) ab. Die Funktionsform stellt somit auch sicher, dass die vorhergesagten bedingten Wahrscheinlichkeiten einer Verweigerung zwischen \(0\) und \(1\) liegen.
Wir verwenden predict(), um die vorhergesagte Änderung der Verweigerungswahrscheinlichkeit zu berechnen, wenn \(P/I \ ratio\) von \(0.3\) auf \(0,4\) erhöht wird.
# 1. compute predictions for P/I ratio = 0.3, 0.4predictions <- predict(denyprobit, newdata = data.frame("pirat" = c(0.3, 0.4)), type = "response")# 2. Compute difference in probabilitiesdiff(predictions)#> 2 #> 0.06081433Wir finden heraus, dass eine Erhöhung des Verhältnisses von Zahlungen zu Einkommen von \(0,3\) auf \(0,4\) die Wahrscheinlichkeit einer Verweigerung um ungefähr \(6.2\%\).
Wir fahren fort, indem wir ein erweitertes Probit-Modell verwenden, um den Effekt der Rasse auf die Wahrscheinlichkeit der Ablehnung eines Hypothekenantrags zu schätzen.
denyprobit2 <- glm(deny ~ pirat + black, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die geschätzte Modellgleichung lautet
Während alle Koeffizienten hochsignifikant sind, sind sowohl die geschätzten Koeffizienten für das Verhältnis von Zahlungen zu Einkommen als auch der Indikator für afroamerikanische Abstammung positiv. Auch hier sind die Koeffizienten schwer zu interpretieren, aber sie deuten darauf hin, dass erstens Afroamerikaner eine höhere Ablehnungswahrscheinlichkeit haben als weiße Antragsteller, wenn man das Verhältnis der Zahlungen zum Einkommen konstant hält, und zweitens, dass Antragsteller mit einem hohen Verhältnis der Zahlungen zum Einkommen ein höheres Risiko haben, abgelehnt zu werden.
Wie groß ist der geschätzte Unterschied in der Ablehnungswahrscheinlichkeit zwischen zwei hypothetischen Antragstellern mit demselben Verhältnis der Zahlungen zum Einkommen? Wie zuvor können wir predict() verwenden, um diese Differenz zu berechnen.
# 1. compute predictions for P/I ratio = 0.3predictions <- predict(denyprobit2, newdata = data.frame("black" = c("no", "yes"), "pirat" = c(0.3, 0.3)), type = "response")# 2. compute difference in probabilitiesdiff(predictions)#> 2 #> 0.1578117In diesem Fall beträgt die geschätzte Differenz der Ablehnungswahrscheinlichkeiten etwa \(15.8\%\).