Einführung
Elastische Eigenschaften spielen eine wichtige Rolle bei einer Reihe von Membranprozessen, wie z.B. der Membranfusion (Chernomordik und Kozlov, 2008) und Modulationen von Membrankanalaktivitäten (Schmidt und MacKinnon, 2008; Sansom und Biggin, 2010; Mashaghi et al., 2013b). In Zellen werden die äußeren Membranen durch die darunter liegenden Aktin-Netzwerke gestützt. Auf Längenskalen, die größer sind als die Maschenweite des Aktinnetzwerks (30-300 nm), wird die mechanische Belastung dann durch das zugehörige Aktin-Zytoskelett dominiert (Morone et al., 2006). Auf kleinen Längenskalen hingegen dominiert der Beitrag der Lipiddoppelschicht. Daher wurden Anstrengungen unternommen, die mechanischen Eigenschaften von Doppelschicht-Patches mit Abmessungen nahe der Maschengröße des Aktin-Zytoskeletts zu untersuchen (Claesson et al., 2011).
Wenn man eine Membran als zweidimensionalen Körper betrachtet, d.h. ihre Dicke vernachlässigt, können ihre mechanischen Eigenschaften bei Abwesenheit von Anisotropien durch zwei elastische Konstanten gemäß der Kontinuumselastizitätstheorie charakterisiert werden. In der gängigen Praxis der Materialcharakterisierung sind diese Parameter typischerweise der Elastizitätsmodul und die Poissonzahl. Abschätzungen für den Elastizitätsmodul von Membranen wurden durch Experimente geliefert (Tierney et al., 2005; Popescu et al., 2006). Allerdings ist die Messung der Poissonzahl aufgrund der geringen Dicke von Membranen im Nanometerbereich nicht einfach (Mitchell et al., 2003; Martins et al., 2009). Aus theoretischer Sicht werden die mechanischen Eigenschaften von Lipidmembranen üblicherweise auf der Basis des Helfrich-Hamiltonschen untersucht. Die wichtigste physikalische Größe, die aus solchen Studien gewonnen wird, ist die Biegesteifigkeit. Der Elastizitätsmodul und die Poissonzahl sind durch Formeln miteinander verbunden, die die Biegesteifigkeit einbeziehen, aber weder Elastizitätsmodul noch Poissonzahl wurden bisher separat bestimmt.
Simulationen und theoretische Modelle wurden verwendet, um wichtige Informationen über elastische (Goetz und Lipowsky, 1998; Lindahl und Edholm, 2001; Ayton et al., 2002) und viskose Eigenschaften von Lipiddoppelschichten (Jeon und Voth, 2005) zu erhalten. Die Untersuchung der mechanischen Eigenschaften von dünnen Filmen ist nicht auf Biomembranen beschränkt und stellt ein aktives Forschungsgebiet in der Materialwissenschaft dar. Es wurden Anstrengungen unternommen, die Poissonzahl von Filmen aus verschiedenen Materialien mit Hilfe von Computersimulationen vorherzusagen. Zum Beispiel haben Galvao et al. Molekulardynamiksimulationen unter Verwendung reaktiver empirischer Bindungsordnungspotentiale eingesetzt, um die mechanischen Eigenschaften von Graphen-Nanobändern zu untersuchen (Martins und Galvao, 2010). Baughman et al. schlugen ein Modell zur Abschätzung der Poissonzahl von Fasernetzwerken vor und wandten es erfolgreich auf Kohlenstoffnanoröhrenblätter (Buckypaper) an (Hall et al., 2008).
In dieser Arbeit stellen wir eine Methode zur Bestimmung der Poissonzahl ν in Simulationen vor und wenden sie auf das grobkörnige Lipidmembranmodell an, das von Lenz und Schmid (2005) eingeführt wurde. Diese Methode ist allgemein und auf beliebige andere Oberflächen anwendbar. Nach der Bestimmung der Biegesteifigkeit kc aus dem Leistungsspektrum der Membranhöhenfluktuationen sind wir in der Lage, den Elastizitätsmodul E zu berechnen.
Materialien und Methoden
Monte-Carlo-Simulationen von Lipiddoppelschichten mit periodischen Randbedingungen in lateralen Richtungen wurden für das von Lenz und Schmid (2005) eingeführte grobkörnige Modell durchgeführt. In diesem Modell werden Single-Tail-Amphiphile betrachtet, die durch sechs Tail-Beads und ein etwas größeres Head-Bead (mit einem Größenverhältnis von 1-1,1) dargestellt werden. Die zu einem Molekül gehörenden Perlen sind über endlich dehnbare nichtlineare elastische (FENE) Federn (Grest und Kremer, 1986) mit einem Bindungsstreckungspotential verbunden Abbildung 1:
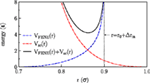
Abbildung 1. Im Modell verwendete Wechselwirkungen.
Hier ist r der Abstand zwischen benachbarten Perlen, νFENE charakterisiert die Stärke der Feder, r0 ist die optimale Bindungslänge (keine Dehnung), und Δrm ist der maximale Dehnungsabstand. Die Steifigkeit der Schwänze wird durch ein harmonisches Bindungswinkelpotential berücksichtigt
wobei θijk der Bindungswinkel ist, der mit drei benachbarten Perlen verbunden ist. Sowohl die nicht gebundenen Perlen, die zum selben Molekül gehören, als auch die Perlen, die zu verschiedenen Molekülen gehören, interagieren über ein Soft-Core-Potential:
wobei θ(.) die Heaviside-Stufenfunktion ist. Die Lösungsmittelmoleküle werden durch ein Phantommodell von Kügelchen repräsentiert, die mit den Lipidkügelchen über VSC(r) (mit den gleichen Parametern wie die Kopfkügelchen) wechselwirken, aber nicht mit sich selbst wechselwirken. Alle Modellparameter wurden entsprechend dem referenzierten Modell (Lenz und Schmid, 2005) gewählt und sind in Tabelle 1 zusammengefasst.

Tabelle 1. Wechselwirkungspotentiale des referenzierten Modells und zugehörige Parameter.
Lipid-Doppelschichten weisen ein reiches Spektrum an Strukturen und Phasenübergängen auf (Nagle und Tristram-Nagle, 2000; Illya et al., 2005; Seto et al., 2008; Thakkar et al., 2011). Der flüssige Zustand bei hohen Temperaturen ist durch eine ungeordnete Anordnung der Lipidschwänze und eine vergleichsweise hohe Lipidmobilität gekennzeichnet. Bei Abkühlung erfährt dieser flüssige Zustand einen Phasenübergang in einen Gelzustand, in dem die Lipidmoleküle geordneter sind und eine geringere Mobilität aufweisen. Weitere mögliche Phasen sind die interdigitale Phase, in der sich Lipidschwänze aus gegenüberliegenden Monolagen gegenseitig durchdringen.
Durch Scannen des Phasendiagramms des referenzierten Modells (Lenz, 2007) haben wir zunächst Lipiddoppelschichten für etwa zwei Millionen Monte-Carlo-Schritte (MC) äquilibriert, um verschiedene Phasen für das Ziel dieser Arbeit zu erzeugen, siehe Abbildung 2. In den reduzierten Einheiten, ϵ/kB für die Temperatur T und ϵ/σLJ3 für den Druck P, sind die entsprechenden thermodynamischen Größen: P = 2 und T = 1,08 für die Gelphase, P = 1 und T = 1,3 für die flüssige Phase, P = 0,5 und T = 1,16 für die interdigitale Phase. Die charakteristischen Parameter für die verschiedenen Phasen, einschließlich der durchschnittlichen Kettenlänge l¯, der Dicke der Doppelschicht d, der Fläche pro Lipid A und des Kettenordnungsparameters Sz sind in Tabelle 2 zusammengefasst.

Abbildung 2. Schnappschüsse der simulierten Lipidmembran in der (A) Gel-, (B) Flüssig- und (C) Interdigit-Phase. Die Kopfperlen und die Schwanzperle des Lipids sind in rot bzw. grün dargestellt.
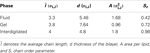
Tabelle 2. Charakteristische Parameter der Lipiddoppelschichten.
Simulationen wurden unter konstanten Temperatur- und Druckbedingungen (NPT-Ensemble) für Lipiddoppelschichten mit unterschiedlichen Größen durchgeführt. Zur Untersuchung des Leistungsspektrums der Oberflächenhöhenfluktuationen simulierten wir einen Bilayer, dessen obere und untere Blättchen aus 64 × 64 Lipidmolekülen bestehen. Für das Lösungsmittelmodell wurden etwa 17000-72000 Perlen gewählt (die genaue Anzahl hängt von der simulierten Phase ab). Um die Analyse der Poissonzahl durchzuführen, haben wir rechteckige Doppelschichten, die aus 12 × 24 Lipidmolekülen pro Leaflet bestehen, in drei verschiedene Phasen äquilibriert.
Um sowohl E als auch ν zu bestimmen, müssen wir eine dieser elastischen Konstanten separat bestimmen. Unter Ausnutzung der periodischen Randbedingungen führen wir eine Methode ein, um die Poissonzahl für die Oberfläche zu berechnen (Abedpour et al., 2010). Die Poissonzahl ist das negative Verhältnis der Querdehnungsänderungen geteilt durch die axialen Dehnungsänderungen in einem Körper, wenn er entlang der axialen Richtung unter der Spannung unterhalb der Proportionalitätsgrenze gedehnt oder gestaucht wird. Für die infinitesimalen Querdehnungen kann die Poissonzahl durch das Verhältnis der relativen Längenänderungen als νij = -ΔLi/ηjLi ersetzt werden, wobei ηj ≡ ΔLj/Lj als der Bruchteil der axialen Längenänderung definiert ist. Dabei ist i ≠ j und i = x, y und z. In der hier vorgestellten Methode wird die Länge zwischen benachbarten Lipiden um einen Faktor (1 + η) in axialer Richtung, sagen wir y-Richtung, umskaliert und die anschließende Änderung der Simulationsboxgröße in senkrechten Richtungen, in diesem Fall x- und z-Richtung, überwacht. Während die umskalierte Boxlänge (1 + η) Ly konstant gehalten wird, um den Druck in den Simulationen zu fixieren, dürfen die Boxabmessungen nun nur in x- und z-Richtung schwanken. Wenn die anfänglichen mittleren Längen in x- und z-Richtung Lx und Lz waren, werden nach der Reskalierung neue mittlere Werte von Lx + ΔLx und Lz + ΔLz erreicht, indem das System für eine geringe Anzahl von MC-Schritten re-equilibriert wird, siehe Abbildung 3.

Abbildung 3. Schnappschüsse der Lipidmembran in flüssiger Phase als (A) Ausgangskonfiguration, (B) nach Vergrößerung der Doppelschicht in y-Richtung um den Faktor (1 + η) und (C) die entspannte Doppelschicht mit Fixierung der Membrangröße in y-Richtung und variabler x-Richtung. Als Folge der positiven Poissonzahl für die Doppelschicht in dieser Phase wird die Membrangröße in x-Richtung reduziert und gleicht sich nach einigen MC-Schritten aus. Die Kopf- und Schwanzperlen des Lipids sind in rot bzw. grün dargestellt.
Während der Simulation haben wir die Temperatur im System leicht erhöht, um den Thermalisierungsvorgang nach der Erweiterung der Box in axialer Richtung zu beschleunigen, was zu einer größeren Mobilität der Partikel führt. Für die flüssige Phase setzten wir die Anfangstemperatur auf T = 1,3 und änderten sie dann für etwa 400 zusätzliche Schritte auf T = 1,4 und schalteten dann wieder auf den ursprünglichen Wert zurück. In ähnlicher Weise wurden für die Gel- und die interdigitalen Phasen die Anfangstemperaturen auf T = 1,08 und T = 1,16 gesetzt und dann auf T = 1,2 bzw. T = 1,3 umgeschaltet.
Eine übliche Analyse der elastischen Eigenschaften einer Membran beruht auf dem Helfrich-Hamiltonschen (Helfrich, 1973), der die Kosten der elastischen freien Enthalpie in Verbindung mit Fluktuationen der Membranhöhe (Abweichungen von der ebenen Oberfläche) beschreibt. Bei Parametrisierung der Membran in kartesischen Koordinaten (x,y) →(x,y,h(x,y)) (Monge-Eichung), ist der Helfrich-Hamiltonian für kleine Fluktuationen gegeben durch
wobei kc die Biegesteifigkeit und σ die Oberflächenspannung ist. Gleichung (4) wird angewendet, wenn die Membran als Körper mit der Dicke Null betrachtet wird. Eine verallgemeinerte elastische Theorie für Membranen mit endlichen Dicken wurde von Brannigan und Brown (2006) vorgeschlagen und kürzlich auf das Lenz-Schmid-Modell angewendet (West et al., 2009; Neder et al, 2010).
Um h(x, y) aus den Simulationen zu bestimmen, diskretisierten wir die (x, y)-Ebene in ein regelmäßiges Gitter mit dem Abstand 2σLJ, bestimmten in jeder Zelle (i, j) die mittleren z-Koordinaten z+(i, j) und z-(i, j) der Kopfwülste im oberen bzw. unteren Fiederblatt und berechneten die Höhe h(i, j) – /2 (der Mittelwert h¯ wurde anschließend subtrahiert). Für eine Membran der Seitengröße L × L sagt Gl. (4) vorhersagen:
für das Leistungsspektrum der Fluktuationen, wobei ĥ(q) die Fouriertransformierte von h(x, y) bei Wellenvektor q, q = |q|, und <> einen Gleichgewichtsmittelwert bezeichnet. In der Numerik wird ĥ(q) aus einer diskreten Fourier-Transformation von h(i, j) berechnet. Es ist klar, dass Gl. (5) nur für einen q-Bereich 2π/L ≪ q ≪ 2π/σLJ gelten kann, in dem weder die endliche Systemgröße noch die (atomistische) Perlengröße die Fluktuationen beeinflusst. Der entsprechende q-Bereich für in vernünftiger Rechenzeit erreichbare Systemgrößen ist leider nicht groß, aber Fits von < |ĥ(q)|2 > ∕kBTL2 als Funktion von q2 in einem Bereich 0.5 ≤ q2 ≤ 1 ergeben eine gute Übereinstimmung mit Gl. (5) für unsere Größen.
Ergebnisse und Diskussionen
In Tabelle 3 sind die erhaltenen Poisson-Verhältnisse νyx, νzx und νxy sowie νzy für verschiedene Phasen zusammengefasst. Wie in Abbildung 4 gezeigt, ist die so erhaltene Poissonzahl unabhängig vom Reskalierungsfaktor η, solange η weder zu groß ist, was zur Zerstörung der Membranstruktur führt, noch zu klein, was nicht genügend Freiraum für die Bewegung der Partikel erzeugt. Gemäß Tabelle 3 und Abbildung 4 haben die flüssige und die interdigitale Phase die gleiche gemessene Poissonzahl für beide x- und y-Richtungen. Das bedeutet, dass diese beiden Phasen in der Ebene der Doppelschicht isotrop sind. Für die Gelphase ist dies jedoch nicht mehr der Fall. Die Messungen zeigen, dass sich ein Bilayer in der Gelphase wie ein anisotropes Material verhält, das zwei deutlich unterschiedliche Werte für die beiden verschiedenen Richtungen in der Ebene des Bilayers hat.

Tabelle 3. Elastische Konstanten, erhalten aus Simulationen von Lipidmembranen in verschiedenen Phasen.

Abbildung 4. Relaxation von -ΔLi/ηjLi in (A) flüssiger, (B) interdigitaler und (C) Gelphase. Der Plateauwert, der nach etwa 5000 MC-Schritten erreicht wird, ergibt unabhängig vom Wert von η die Poissonzahl ν. In der Gelphase hat die Poissonzahl unterschiedliche Werte für νxy und νyx und diese Phase wirkt als anisotrope Oberfläche.
Umgekehrt reorganisieren sich die Lipide bei der Ausdehnung der Doppelschicht in der senkrechten Richtung zur Kippebene so, dass die Doppelschicht seitlich schrumpft. Für die vorliegende Arbeit wurden die Bindungslängen der Lipide in z-Richtung (senkrecht zur Bilayer-Ebene) nicht neu skaliert. Der Grund dafür ist, dass zur Beobachtung des Poisson-Effekts die Länge zwischen den Kügelchen um einen Faktor reskaliert werden sollte, der genügend Platz für die Umlagerung der Partikel schafft. In z-Richtung sollte diese Vergrößerung jedoch zwischen den gebundenen Kügelchen innerhalb eines Lipids stattfinden, was einen Bindungsbruch verursacht. Die angegebenen Werte für νzx und νzy sind die resultierenden relativen Längenänderungen in der mittleren Länge der Doppelschicht aufgrund der lateralen Ausdehnung der Doppelschicht in x- bzw. y-Richtung.
Die erhaltenen Werte für die Biegesteifigkeit kc betragen 5,2ϵ für die flüssige Phase und 7,6ϵ für die interdigitale Phase. Für die Gel- und die Fluidphase stimmen die Ergebnisse mit den bisherigen rechnerischen Berichten (West, 2008; West et al., 2009) und experimentellen Befunden (Falcioni et al., 1997; Liu und Zhang, 2009) überein. Die Spektraldichte für die interdigitale Phase wurde nach der gleichen Methode berechnet. Wir berichten hier über die Biegesteifigkeit für die interdigitalisierte Phase. Abbildung 5 zeigt die Fluktuationsspektren der Höhe für die drei untersuchten Phasen und passt an die Gleichung (5).
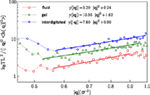
Abbildung 5. Fluktuationsspektren für die flüssige, die Gel- und die interdigitale Phase und Fits zu Gl. (5).
In der zweidimensionalen Elastizitätstheorie ist die Biegesteifigkeit kc mit der Poissonzahl ν und dem Elastizitätsmodul E nach (Landau et al, 1986)
wobei d die mittlere Membrandicke ist, für die wir 5,48σLJ bzw. 4,86σLJ für die flüssige und die interdigitale Phase erhalten. Setzt man die gefundenen Werte für die Poissonzahlen und die Biegesteifigkeiten für Doppelschichten in zwei isotropen Phasen in Gleichung (6) ein, erhält man die entsprechenden Youngschen Module. Die so berechneten Elastizitätsmodule betragen 0,28 und 0,67 in Einheiten von ϵ/σ3 für den flüssigen bzw. interdigitalen Zustand. Offensichtlich erlaubt die beobachtete Anisotropie in der Gelphase nicht, das obige Theorem für die Doppelschicht in dieser Phase zu verwenden.
Der in diesem Artikel vorgestellte Ansatz könnte auf Membranen mit komplexeren Lipidzusammensetzungen angewendet werden, vorausgesetzt, dass die experimentell verifizierten Wechselwirkungsmodelle für diese Lipide existieren. Der Ansatz könnte auch mit genaueren Simulationen von Doppelschichten kombiniert werden. Vollständige atomistische Simulationen und insbesondere ab initio-Simulationen könnten prinzipiell genauere Beschreibungen des Systems liefern, sind aber mit einem enormen Rechenaufwand verbunden (Mashaghi et al., 2012, 2013a).
Schlussfolgerung
Wir haben Monte-Carlo-Simulationen des grobkörnigen Lipid-Doppelschichtmodells durchgeführt, um Einblicke in die mechanischen Eigenschaften von planaren Lipidmembranen zu gewinnen. Durch die Verwendung einer Reskalierungsmethode konnten wir zusätzlich zur Biegesteifigkeit, die aus einer Analyse der Membranhöhenfluktuationen auf Basis des Helfrich-Hamiltonschen bestimmt wurde, die Poissonzahl ν für verschiedene Phasen bestimmen. Dies erlaubt uns, auch den E-Modul E für verschiedene Phasen zu berechnen. Der Ansatz ist genau, einfach zu implementieren und kann auf andere Membranen wie Graphen (Abedpour et al., 2010) angewendet werden, um die Temperaturabhängigkeit der Poissonzahl und des E-Moduls vorherzusagen. Andere interessante Systeme, die untersucht werden sollen, sind kristalline metallische Nanodrähte, bei denen der Elastizitätsmodul ihre strukturelle Leistung und ihr funktionelles Verhalten kontrolliert, wie z. B. ihre Resonanzfrequenz unter oszillierender Last, die typischerweise während der Betätigung und Sensorik angewendet wird (Chen et al., 2006; McDowell et al, 2008).
Conflict of Interest Statement
Die Autoren erklären, dass die Forschung in Abwesenheit jeglicher kommerzieller oder finanzieller Beziehungen durchgeführt wurde, die als potenzieller Interessenkonflikt ausgelegt werden könnten.
Acknowledgments
Wir möchten Philipp Maass für seine hilfreichen Diskussionen danken.
Abedpour, N., Asgari, R., und Tabar, M. R. R. (2010). Irreversibilität in Reaktion auf Kräfte, die auf Graphenblätter wirken. Phys. Rev. Lett. 104, 196804. doi:10.1103/PhysRevLett.104.196804
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Ayton, G., Smondyrev, A., Bardenhagen, S., McMurtry, P., and Voth, G. (2002). Berechnung des Volumenmoduls für eine Lipid-Doppelschicht mit Nicht-Gleichgewichts-Molekulardynamik-Simulation. Biophys. J. 82, 1226-1238. doi:10.1016/S0006-3495(02)75479-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Brannigan, G., and Brown, F. L. H. (2006). Ein konsistentes Modell für thermische Fluktuationen und proteininduzierte Verformungen in Lipiddoppelschichten. Biophys. J. 90, 1501. doi:10.1529/biophysj.105.075838
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chen, C., Shi, Y., Zhang, Y., Zhu, J., and Yan, Y. (2006). Größenabhängigkeit des Elastizitätsmoduls in ZnO-Nanodrähten. Phys. Rev. Lett. 96, 075505. doi:10.1103/PhysRevLett.96.075505
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chernomordik, L. V., and Kozlov, M. M. (2008). Mechanik der Membranfusion. Nat. Struct. Mol. Biol. 15, 675-683. doi:10.1038/nsmb.1455
CrossRef Full Text
Claesson, M., Frost, R., Svedhem, S., and Andersson, M. (2011). Porenüberbrückende Lipid-Doppelschichten auf mesoporösem Siliziumdioxid mit variierender Porengröße. Langmuir 27, 8974-8982. doi:10.1021/la201411b
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Falcioni, M., Bowick, M. J., Guitter, E., and Thorleifsson, G. (1997). Die Poissonzahl von kristallinen Oberflächen. Europhys. Lett. 38, 67-72. doi:10.1016/j.jhazmat.2010.12.101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Goetz, R., und Lipowsky, R. (1998). Computersimulationen von Doppelschichtmembranen: Selbstassemblierung und Grenzflächenspannung. J. Chem. Phys. 108, 7397-7409. doi:10.1063/1.476160
CrossRef Full Text
Grest, G. S., and Kremer, K. (1986). Molekulardynamische Simulation für Polymere in Gegenwart eines Wärmebades. Phys. Rev. A 33, 3628-3631. doi:10.1103/PhysRevA.33.3628
CrossRef Full Text
Hall, L., Coluci, V., Galvao, D., Kozlov, M., Zhang, M., Dantas, S., et al. (2008). Vorzeichenwechsel der Poissonzahl für Kohlenstoff-Nanoröhrenblätter. Science 320, 504-507. doi:10.1126/science.1149815
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Helfrich, W. (1973). Elastische Eigenschaften von Lipiddoppelschichten – Theorie und mögliche Experimente. Z. Naturforsch. C 28, 693.
Illya, G., Lipowsky, R., and Shillcock, J. C. (2005). Einfluss von Kettenlänge und Asymmetrie auf die Materialeigenschaften von Doppelschichtmembranen. J. Chem. Phys. 122, 1-6. doi:10.1063/1.1917794
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Jeon, J., and Voth, G. (2005). Die dynamischen Stressantworten auf Flächenänderungen in planaren Lipid-Doppelschichtmembranen. Biophys. J. 88, 1104-1119. doi:10.1529/biophysj.104.052183
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Landau, L. D., Pitaevskii, L. P., Lifshitz, E. M., and Kosevich, A. M. (1986). Theory of Elasticity, Volume 7, 3rd Edn. Oxford: Butterworth-Heinemann.
Lenz, O. (2007). Computersimulation von Lipiddoppelschichten. Dissertation, Universität Bielefeld, Bielefeld.
Lenz, O., und Schmid, F. (2005). Ein einfaches Computermodell für flüssige Lipiddoppelschichten. J. Mol. Liq. 117, 147-152. doi:10.1016/j.molliq.2004.08.008
CrossRef Full Text
Lindahl, E., and Edholm, O. (2001). Molekulardynamische Simulation von NMR-Relaxationsraten und langsamer Dynamik in Lipid-Doppelschichten. J. Chem. Phys. 115, 4938-4950. doi:10.1529/biophysj.107.121806
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Liu, P., and Zhang, Y. W. (2009). Temperaturabhängige Biegesteifigkeit von Graphen. Appl. Phys. Lett. 94, 231912. doi:10.1063/1.3155197
CrossRef Full Text
Martins, B., and Galvao, D. (2010). Gekrümmte Graphen-Nanobänder: Struktur und Dynamik von Kohlenstoff-Nanoblechen. Nanotechnology 21, 075710. doi:10.1088/0957-4484/21/7/075710
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Martins, P., Malhaire, C., Brida, S., und Barbier, D. (2009). On the determination of Poisson’s ratio of stressed monolayer and bilayer submicron thick films. Microsyst. Technol. 15, 1343-1348. doi:10.1007/s00542-009-0822-5
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mashaghi, A, Partovi-Azar, P., Jadidi, T., Nafari, N., Esfarjani, K., Maass, P., et al. (2012). Interfacial water facilitates energy transfer by inducing extended vibrations in membrane lipids. J. Phys. Chem. B 116, 6455-6460. doi:10.1021/jp302478a
CrossRef Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Anvari, M., Panahian, J. S., Nafari, N., et al. (2013a). Enhanced autoionization of water at phospholipid interfaces. J. Phys. Chem. C 117, 510-514. doi:10.1021/jp3119617
CrossRef Full Text
Mashaghi, S., Jadidi, T., Koenderink, G., and Mashaghi, A. (2013b). Lipid nanotechnology. Int. J. Mol. Sci. 14, 4242-4282. doi:10.3390/ijms14024242
CrossRef Full Text
McDowell, M., Leach, A., and Gall, K. (2008). Über den Elastizitätsmodul von metallischen Nanodrähten. Nano Lett. 8, 3613-3618. doi:10.1021/nl801526c
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mitchell, J. S., Zorman, C. A., Kicher, T., Roy, S., and Mehregany, M. (2003). Untersuchung des Bulge-Tests zur Bestimmung der Eigenspannung, des Elastizitätsmoduls und der Poissonzahl von 3c-sic Dünnschichten. J. Aerosp. Eng. 16, 46-54. doi:10.1061/(ASCE)0893-1321(2003)16:2(46)
CrossRef Full Text
Morone, N., Fujiwara, T., Murase, K., Kasai, R. S., Ike, H., Yuasa, S., et al. (2006). Dreidimensionale Rekonstruktion des Membranskeletts an der Plasmamembran-Grenzfläche durch Elektronentomographie. J. Cell Biol. 174, 851-862. doi:10.1083/jcb.200606007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Nagle, J. F., and Tristram-Nagle, S. (2000). Structure of lipid bilayers. Biochim. Biophys. Acta 1469, 159-195. doi:10.1016/S0304-4157(00)00016-2
CrossRef Full Text
Neder, J., West, B., Nielaba, P., and Schmid, F. (2010). Grobkörnige Simulationen von Membranen unter Spannung. J. Chem. Phys. 132, 115101. doi:10.1063/1.3352583
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Popescu, G., Ikeda, T., Goda, K., Best-Popescu, C. A., Laposata, M., Manley, S., et al. (2006). Optische Messung der Zellmembranspannung. Phys. Rev. Lett. 97, 218101. doi:10.1103/PhysRevLett.97.218101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Sansom, D. M. S. P., und Biggin, P. C. (2010). Molecular Simulations and Biomembranes: From Biophysics to Function, 1st Edn. Cambridge, UK: Royal Society of Chemistry.
Schmidt, D., und MacKinnon, R. (2008). Spannungsabhängiges k+-Kanal-Gating und Spannungssensor-Toxin-Empfindlichkeit hängen vom mechanischen Zustand der Lipidmembran ab. Proc. Natl. Acad. Sci. U.S.A. 105, 19276-19281. doi:10.1073/pnas.0810187105
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Seto, H., Yamada, N., Nagao, M., Hishida, M., and Takeda, T. (2008). Bending modulus of lipid bilayers in a liquid-crystalline phase including anomalous swelling regime estimated by neutron spin echo experiments. Eur. Phys. J. E Soft Matter 26, 217-223. doi:10.1140/epje/i2007-10315-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Thakkar, F. M., Maiti, P., Kumarana, V., and Ayappa, K. (2011). Verifizierung von Skalierungen für die Biegesteifigkeit von Doppelschichtmembranen mit Hilfe von mesoskaligen Modellen. Soft Matter 7, 3963-3966. doi:10.1039/c0sm00876a
CrossRef Full Text
Tierney, K. J., Block, D. E., and Longo, M. L. (2005). Elastizität und Phasenverhalten von DPPC-Membranen moduliert durch Cholesterin, Ergosterol und Ethanol. Biophys. J. 89, 2481-2493. doi:10.1529/biophysj.104.057943
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
West, B. (2008). Lipid-Protein-Wechselwirkungen in Lipidmembranen. Dissertation, Universität Bielefeld, Bielefeld.
West, B., Brown, F. L. H., and Schmid, F. (2009). Membran-Protein-Wechselwirkungen in einem generischen grobkörnigen Modell für Lipid-Doppelschichten. Biophys. J. 96, 101. doi:10.1529/biophysj.108.138677
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text