Nachdem wir definiert haben, dass die logarithmische Funktion y = log b x die Umkehrfunktion der Exponentialfunktion y = b x ist, können wir nun zur grafischen Darstellung logarithmischer Funktionen übergehen, indem wir die Beziehung zwischen Exponential- und Logarithmusfunktionen betrachten.
Aber bevor wir uns in das Thema der grafischen Darstellung logarithmischer Funktionen stürzen, ist es wichtig, dass wir uns mit den folgenden Begriffen vertraut machen:
- Der Bereich einer Funktion
Der Bereich einer Funktion ist eine Menge von Werten, die Sie in der Funktion ersetzen können, um eine akzeptable Antwort zu erhalten.
- Der Bereich einer Funktion
Dies ist die Menge der Werte, die Sie erhalten, nachdem Sie die Werte im Bereich durch die Variable ersetzt haben.
- Asymptoten
Es gibt drei Arten von Asymptoten, nämlich: vertikale, horizontale und schräge. Die vertikale Asymptote ist der Wert von x, bei dem die Funktion in der Nähe unbegrenzt wächst.
Horizontale Asymptoten sind konstante Werte, denen sich f(x) bei unbegrenzt wachsendem x nähert. Schräge Asymptoten sind Polynome ersten Grades, denen sich f(x) bei unbegrenzt wachsendem x nähert.
Wie stellt man logarithmische Funktionen dar?
Der Graph einer logarithmischen Funktion kann erstellt werden, indem man den Graphen einer Exponentialfunktion betrachtet und dann x und y vertauscht.
Der Graph einer Exponentialfunktion f (x) = b x oder y = b x enthält folgende Merkmale:
- Der Bereich einer Exponentialfunktion sind reelle Zahlen (-unendlich, unendlich).
- Der Bereich ist ebenfalls positive reelle Zahlen (0, unendlich)
- Der Graph einer Exponentialfunktion geht normalerweise durch den Punkt (0, 1). Das bedeutet, dass der y-Achsenabschnitt im Punkt (0, 1) liegt.
- Der Graph einer Exponentialfunktion f(x) = b x hat eine horizontale Asymptote bei y = 0.
- Ein Exponentialgraph nimmt von links nach rechts ab, wenn 0 < b < 1 ist, und dieser Fall wird als exponentieller Zerfall bezeichnet.
- Wenn die Basis der Funktion f(x) = b x größer als 1 ist, dann nimmt ihr Graph von links nach rechts zu und wird exponentielles Wachstum genannt.
Indem wir die obigen Eigenschaften einzeln betrachten, können wir die Eigenschaften von logarithmischen Funktionen wie folgt ableiten:
- Eine logarithmische Funktion hat den Bereich (0, unendlich).
- Der Bereich einer logarithmischen Funktion ist (-unendlich, unendlich).
- Der Graph einer logarithmischen Funktion geht durch den Punkt (1, 0), der bei einer Exponentialfunktion der Kehrwert von (0, 1) ist.
- Der Graph einer logarithmischen Funktion hat eine vertikale Asymptote bei x = 0.
- Der Graph einer logarithmischen Funktion wird von links nach rechts abnehmen, wenn 0 < b < 1.
- Und wenn die Basis der Funktion größer als 1 ist, b > 1, dann steigt der Graph von links nach rechts an.
Wie kann man eine logarithmische Grundfunktion grafisch darstellen?
Eine logarithmische Grundfunktion ist im Allgemeinen eine Funktion ohne horizontale oder vertikale Verschiebung.
Hier sind die Schritte, um einen Graphen einer logarithmischen Grundfunktion zu erstellen.
- Da alle logarithmischen Funktionen durch den Punkt (1, 0) verlaufen, suchen wir diesen und setzen einen Punkt an den Punkt.
- Um zu verhindern, dass die Kurve die y-Achse berührt, zeichnen wir eine Asymptote bei x = 0.
- Wenn die Basis der Funktion größer als 1 ist, erhöhen Sie die Kurve von links nach rechts. Umgekehrt, wenn die Basis kleiner als 1 ist, vermindern Sie die Kurve von links nach rechts.
Betrachten wir nun die folgenden Beispiele:
Beispiel 1
Grafen Sie die logarithmische Funktion f(x) = log 2 x und geben Sie Bereich und Domäne der Funktion an.
Lösung
- Es ist klar, dass eine logarithmische Funktion den Bereich und die Reichweite von (0, unendlich) und (-unendlich, unendlich)
- Da die Funktion f(x) = log 2 x größer als 1 ist, erhöhen wir unsere Kurve von links nach rechts, wie unten gezeigt.
- Die vertikale Asymptote bei x = 0 können wir nicht sehen, weil sie von der y-Achse verdeckt wird.
Beispiel 2
Zeichnen Sie einen Graphen von y = log 0,5 x
Lösung
- Setzen Sie einen Punkt an den Punkt (1, 0). Alle logarithmischen Kurven gehen durch diesen Punkt.
- Zeichnen Sie eine Asymptote bei x = 0.
- Da die Basis der Funktion y = log 5 x kleiner als 1 ist, werden wir unsere Kurve von links nach rechts abnehmen.
- Die Funktion y = log 5 x wird auch (0, unendlich) und (-unendlich, unendlich) als Domäne und Bereich haben.
Darstellung einer logarithmischen Funktion mit horizontaler Verschiebung
Logarithmische Funktionen mit horizontaler Verschiebung haben die Form f(x) = log b (x + h) oder f (x) = log b (x – h), wobei h die horizontale Verschiebung ist. Das Vorzeichen der horizontalen Verschiebung bestimmt die Richtung der Verschiebung. Wenn das Vorzeichen positiv ist, wird die Verschiebung negativ, und wenn das Vorzeichen negativ ist, wird die Verschiebung positiv.
Durch die Anwendung der horizontalen Verschiebung werden die Eigenschaften einer logarithmischen Funktion auf folgende Weise beeinflusst:
- Der x-Achsenabschnitt verschiebt sich um eine feste Strecke gleich h nach links oder rechts.
- Die vertikale Asymptote verschiebt sich um einen festen Abstand gleich h.
- Der Bereich der Funktion ändert sich ebenfalls.
Beispiel 3
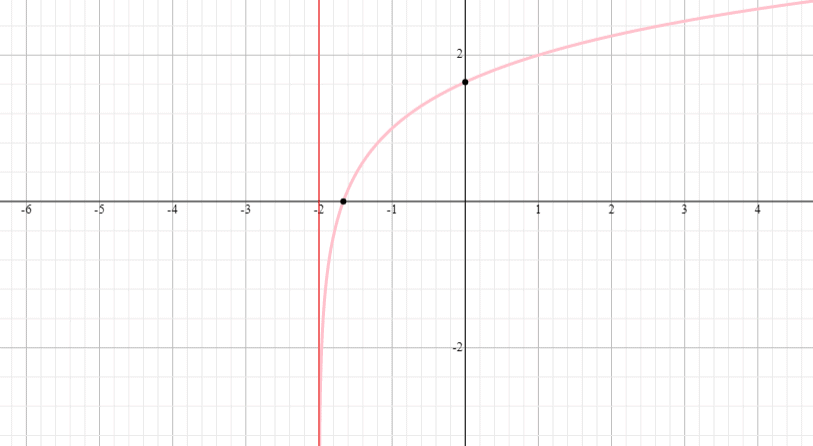
Zeichnen Sie einen Graphen der Funktion f(x) = log 2 (x + 1) und geben Sie den Bereich und die Reichweite der Funktion an.
Lösung
⟹ Bereich: (- 1, unendlich)
⟹ Bereich: (-unendlich, unendlich)
Beispiel 4
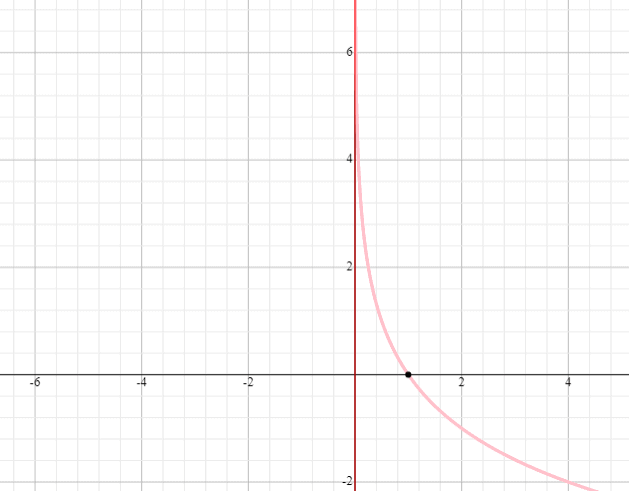
Grafen Sie y = log 0,5 (x – 1) und geben Sie den Bereich und den Bereich an.
Lösung
⟹ Bereich: (1, unendlich)
⟹ Bereich: (-unendlich, unendlich)
Wie kann man eine Funktion mit einer Vertikalen grafisch darstellen?
Eine logarithmische Funktion mit horizontaler und vertikaler Verschiebung hat die Form f(x) = log b (x) + k, wobei k die vertikale Verschiebung ist.
Die vertikale Verschiebung beeinflusst die Eigenschaften einer Funktion wie folgt:
- Der x-Achsenabschnitt verschiebt sich entweder nach oben oder nach unten mit einem festen Abstand von k
Beispiel 5
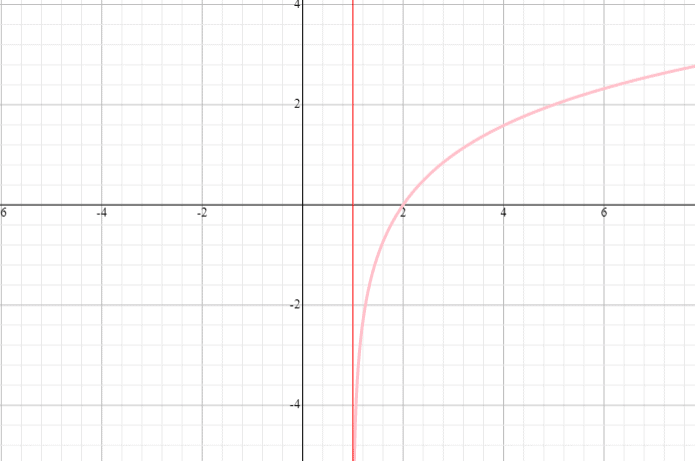
Graphen Sie die Funktion y = log 3 (x – 4) und geben Sie den Bereich und das Gebiet der Funktion an.
Lösung
⟹ Gebiet: (0, unendlich)
⟹ Bereich: (-unendlich, unendlich)
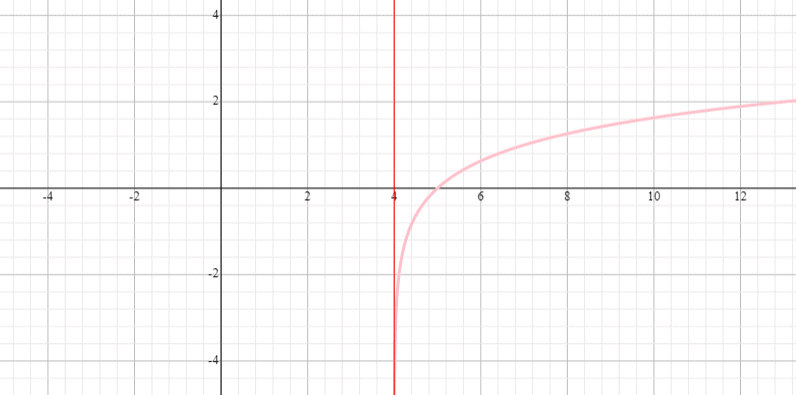
Funktionen mit sowohl horizontaler als auch vertikaler Verschiebung
Eine logarithmische Funktion mit sowohl horizontaler als auch vertikaler Verschiebung hat die Form (x) = log b (x + h) + k, wobei k und h die vertikale bzw. horizontale Verschiebung sind.
Beispiel 6
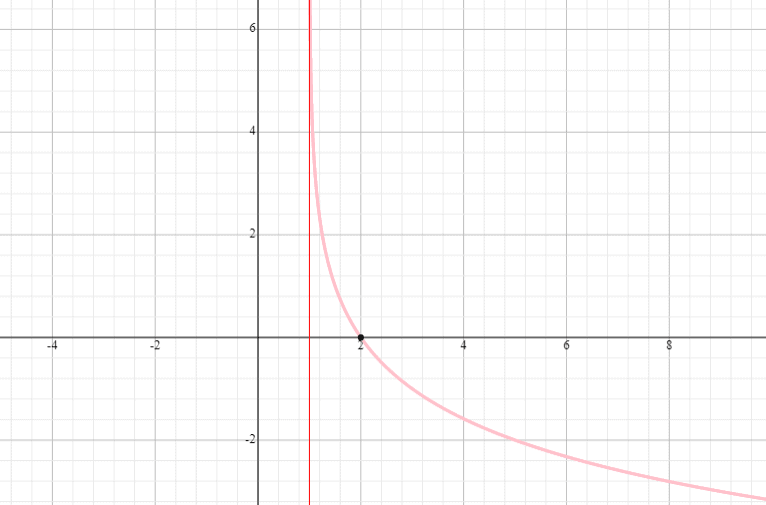
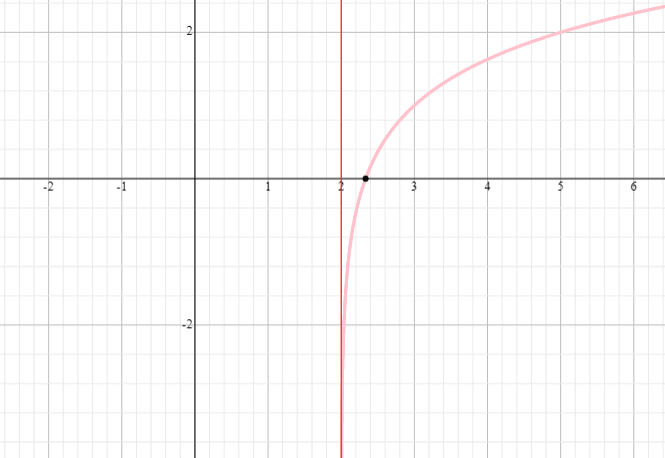
Grafen Sie die logarithmische Funktion y = log 3 (x – 2) + 1 und bestimmen Sie den Definitionsbereich und den Bereich der Funktion.
⟹ Definitionsbereich: (2,unendlich)
⟹ Bereich: (-unendlich, unendlich)
Beispiel 7
Grafen Sie die logarithmische Funktion y = log 3 (x + 2) + 1 und finden Sie den Bereich und den Bereich der Funktion.
S
⟹ Bereich: (- 2,unendlich)
⟹ Bereich: (-unendlich, unendlich)