Berechnen der Impedanz
In Wechselstromkreisen nimmt das Ohmsche Gesetz die allgemeinere Form an: E = I⋅Z, wobei E die Spannung und I der Strom ist, wie zuvor. Der neue Begriff Z ist die Impedanz, eine Vektorkombination aus:
- Widerstand, R (in Ohm), wobei die Spannung phasengleich mit dem Strom abfällt.
- Induktiver Blindwiderstand, XL (in Ohm), wobei die Spannung um 90° vor dem Strom abfällt.
- Kapazitiver Blindwiderstand, XC (in Ohm), mit Spannungsabfällen, die dem Strom um 90° nacheilen.
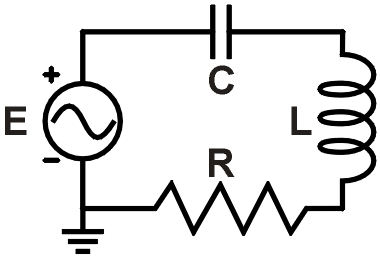
f = 6,4 kHz R = 120 Ω
L = 3,6 mH C = 0,38 μf
Abbildung 1. Beispiel RLC-Schaltung

Abbildung 2. Vektorsumme von R und
XL-XC ergibt Z
Aus den Formeln für XL und XC ist ersichtlich, dass die Reaktanzen sowohl von den Bauteilwerten L und C als auch von der Wechselstromfrequenz f abhängen:
![]() und
und 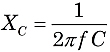
wobei f die Frequenz inHertz (oder sec-1), L die Induktivität in Henries und C die Kapazität in Farad ist. Da XL und X um 180° phasenverschoben sind, ist der Gesamtreaktanzwert X einer Reihenschaltung XL-XC.
Die bekannten Anwendungen des Ohmschen Gesetzes, wie z. B. die Berechnung von Reihen- und Parallelschaltungen, gelten weiterhin. Allerdings müssen Sie nun die konkurrierenden Vektorbeiträge von Widerständen und Reaktanzen berücksichtigen.
Phasenwinkel und Vektoren
Bestimmen wir die Gesamtimpedanz der Schaltung in Abbildung 1. Verwenden Sie dazu die obigen Formeln:
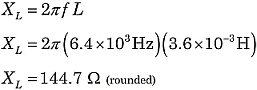 |
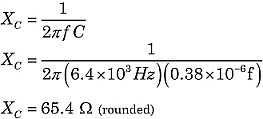 |
Bei der Konstruktion der Impedanz Z, trägt der Widerstand die Horizontalkomponente bei. Die vertikale Komponente ist die Differenz der Reaktanzen: XL-XC.Dann ist Z die Vektorsumme von R und XL-XC,wie in Abbildung 2 dargestellt.
Da Z die Hypotenuse eines rechtwinkligen Dreiecks ist, können wir den Satz des Pythagoras und die Geometrie des rechtwinkligen Dreiecks verwenden, um Z zu berechnen.
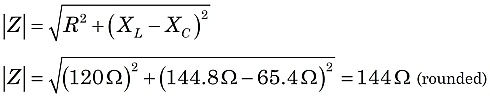
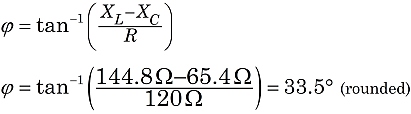
So, in dieser Schaltung eine Impedanz von144 Ohm, wobei der Strom der Versorgungsspannung mit einem Phasenwinkel von 33° nacheilt.5° nacheilt.
Wie Sie aus den obigen Ausführungen ersehen können, ist es durchaus möglich, dass sich die induktiven und kapazitiven Reaktanzen unter den richtigen Kombinationen von L-, C- und f-Werten genau aufheben. Dies ist eine sehr wichtige Bedingung, die als Resonanz bekannt ist.