En aplicaciones de ingeniería, nos encontramos frecuentemente con funciones cuyos valores cambian bruscamente en valores específicos de tiempo t. Un ejemplo común es cuando se enciende o apaga un voltaje en un circuito eléctrico en un valor específico de tiempo t.
Más adelante, en esta página…
Función de paso unitario desplazado
Pulso rectangular
El valor de t = 0 se suele tomar como un tiempo conveniente para encender o apagar la tensión dada.
El proceso de conmutación puede describirse matemáticamente mediante la función denominada Función de Paso Unitario (también conocida como función de Heaviside en honor a Oliver Heaviside).
La Función de Paso Unitario
Definición: La función de paso unitario, `u(t)`, se define como
`u(t)={: {(0, t < 0), (1, t > 0) :}`
Es decir, u es una función del tiempo t, y u tiene valor cero cuando el tiempo es negativo (antes de que accionemos el interruptor); y valor uno cuando el tiempo es positivo (desde que accionamos el interruptor).
¿Valor en t = 0?
En algunos libros de texto verás que la función escalonada unitaria se define con valor 1 en t = 0, de la siguiente manera:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
Indicaríamos la discontinuidad en nuestra gráfica así:
Gráfica de `f(t)=u(t)`, la función escalón unitario, con `f(0) = 1`.
También, a veces, verás el valor dado como `f(0) = 0.5`.
En este trabajo, no supone una gran diferencia para nuestros cálculos, por lo que seguiremos utilizando la primera interpretación, y dibujaremos nuestras gráficas en consecuencia.
Función de paso unitario desplazado
En muchos circuitos, las formas de onda se aplican a intervalos específicos distintos de `t=0`. Una función de este tipo puede describirse mediante la función de paso unitario desplazada (también conocida como retardada).
Definición de la función de paso unitario desplazado
Una función que tiene valor `0` hasta el tiempo `t = a` y a partir de entonces tiene valor `1`, se escribe:
`u(t-a)={{: (0, si, t < a), (1, si, t > a) :}`
Ejemplo 1 – Función de paso unitario desplazado
`f(t) = u(t – 3)`
La ecuación significa que f(t) tiene valor de `0` cuando `t < 3` y `1` cuando `t > 3`.
El esquema de la forma de onda es el siguiente:
Pulso rectangular
Una situación común en un circuito es que se aplique una tensión en un momento determinado (digamos t = a) y se elimine después, en t = b (digamos). Escribimos tal situación usando funciones de paso unitario como:
`V(t) = u(t – a) – u(t – b)`
Este voltaje tiene fuerza `1`, duración `(b – a)`.
Ejemplo 2 – Pulso rectangular
La gráfica de `V(t) = u(t – 1,2) – u(t – 3,8)` es la siguiente. Aquí, la duración es `3,8 – 1,2 = 2,6`.
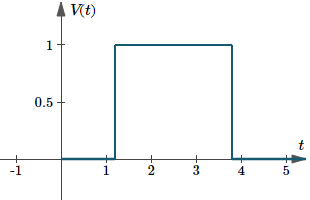
Gráfica de `V(t)=u(t-1.2)-u(t-3.8)`, un ejemplo de pulso rectangular.
Ejercicios
¿Necesitas papel cuadriculado?
Escribe las siguientes funciones en términos de función(es) de paso unitario. Esboza cada forma de onda.
(a) Una fuente de 12 V se enciende en t = 4 s.
Respuesta
Escribimos la función de la siguiente manera:
`V(t)=12-u(t-4)`.
Aquí tienes la gráfica:
Gráfica de `V(t)=12-u(t-4)`, una función escalonada desplazada.
(b) `V(t)={{: (1, 0 < t < a),(0, t > a) :}`
(Supongamos que a > 0.)
Respuesta
En palabras, la tensión tiene valor `1` hasta el tiempo `t = a`. Después se apaga.
Tenemos una situación de «pulso rectangular» y necesitamos utilizar esta fórmula:
`V(t) = u(t – a) – u(t – b)`
En nuestro ejemplo, el pulso comienza en `t = 0`, por lo que usamos `u(t)`, y termina en `t = a`, por lo que usamos `u(t – a)`.
Así que la función requerida es:
`V(t)=1-` `=u(t)-u(t-a)`
Gráfico de `V(t)=u(t)-u(t-a)`, una función de paso unitario desplazado.
(c) Un ciclo de una onda cuadrada, `f(0) = 4`, amplitud = `4`, periodo = `2` segundos.
Respuesta
`f(0) = 4` significa que empezamos en el valor `4`.
Si toda la onda tiene periodo `2`, y es una onda cuadrada, entonces significa que durante la mitad del tiempo, el valor es (positivo) `4` y la otra mitad es `-4`.
Así que para el primer segundo, tiene valor `4`, para el segundo, el valor de la función es `-4`.
Escribimos esto, usando la fórmula del «pulso rectangular» de antes:
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
La gráfica de este primer ciclo es:
Gráfica de `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, una onda cuadrada.
(d) La función rampa unitaria (es decir.`f(t) = t` para `t > 0`)
Respuesta
La función rampa unitaria tiene pendiente `1` , partiendo de `t = 0` , y pasa por `(0, 0)`.
Por tanto, la función de tensión viene dada por:
`V(t) = t – u(t)`
La gráfica de la función es:
Gráfica de `V(t)=t – u(t)`, la función de rampa unitaria.
(e) Un ciclo de una onda diente de sierra (es decir.e. `f(t)=a/b t` para `0 < t < b`. Supongamos que `a > 0`.)
Respuesta
Nuestra gráfica comienza en `t = 0` y tiene pendiente `a / b`. Termina en `t = b`.
Entonces nuestra función será:
`f(t)=a/b t – {u(t)-u(t-b)}`
La gráfica de nuestra función:
Gráfica de `f(t)=a/b t – {u(t)-u(t-b)}`, una forma de onda en diente de sierra.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t 5) :}`
Respuesta
En este ejemplo, nuestra función es `V(t) = 2t + 8` que tiene pendiente `2` e `V`-intercepción `8`.
La señal sólo se enciende entre `t = 3` y `t = 5`. El resto del tiempo está apagada.
Así que nuestra función de voltaje será:
`V(t) `= (2t+8) -{u(t – 3)- u(t – 5)}`
La gráfica es la siguiente:
Gráfico de `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}`. La línea discontinua es `V(t) = 2t + 8`.
Superior
Este solucionador de cálculo puede resolver una amplia gama de problemas matemáticos.
Ir a: Solucionador de cálculo online