Los pies de superficie por minuto, la carga de viruta, el espesor de viruta no formada y el adelgazamiento de viruta son términos familiares en el taller. Sin embargo, en las últimas semanas, varios sucesos en nuestro taller me han hecho ver que hay muchos profesionales del metal que no entienden estos términos y los cálculos que los acompañan. Tanto si trabajas en un pequeño taller como en un gran fabricante por encargo, es importante entender los cálculos de las herramientas de corte y cómo utilizarlos para ayudar a conseguir un aumento significativo de la eficiencia.
Los cálculos de la velocidad de corte podrían ser los más importantes. Son fáciles de usar y, con un poco de explicación, fáciles de entender. La velocidad de corte de una herramienta se expresa en pies de superficie por minuto (sfm) o metros de superficie por minuto (m/min.). Al igual que las mph de un coche, los sfm son la distancia lineal que recorre una herramienta de corte por minuto. Para tener un mejor sentido de la escala, 300 sfm, por ejemplo, se convierten en 3,4 mph.
Los fabricantes de herramientas recomiendan velocidades de corte para diferentes tipos de materiales de las piezas de trabajo. Cuando un fabricante de herramientas sugiere 100 sfm, está indicando que la superficie exterior de la herramienta giratoria debe viajar a una velocidad igual a 100 pies lineales por minuto. Si la herramienta tiene una circunferencia (diámetro × π) de 12″, tendría que girar a 100 rpm para lograr 100 sfm.
Todas las imágenes son cortesía de C. Tate
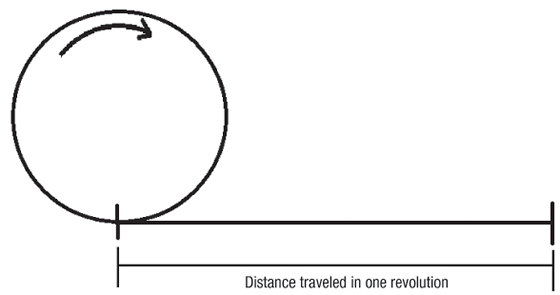
Imagine la herramienta de corte como un anillo o cilindro rodante. La distancia recorrida en una revolución por las rpm es su velocidad superficial. Si el círculo anterior tuviera un diámetro de 3,82″, la circunferencia sería de 12″. Como resultado, cada revolución produciría una distancia lineal de 1′, y una velocidad del husillo de 100 rpm sería una velocidad de corte de 100 sfm.
La siguiente ecuación se utiliza para calcular la velocidad del husillo: rpm = sfm ÷ diame-ter × 3,82, donde el diámetro es el diámetro de la herramienta de corte o el diámetro de la pieza en un torno en pulgadas, y 3.82 es una constante que proviene de una simplificación algebraica de la fórmula más compleja: rpm = (sfm × 12) ÷ (diámetro × π).
Debido a que el diámetro de la herramienta se mide en pulgadas, los «pies» en sfm deben con-vertirse en pulgadas, y como hay 12 pulgadas en un pie, multiplique sfm por 12. Además, la circunferencia de la herramienta se encuentra multiplicando el diámetro de la herramienta por π, o 3,14 para simplificar. El resultado es: rpm = (sfm × 12) ÷ (diámetro × π) = (sfm ÷ diámetro) × (12 ÷ π) = (sfm ÷ diámetro) × 3,82.

Observe las líneas verticales, llamadas marcas de herramienta, en el exterior de la pieza que se está torneando. A medida que aumenta la velocidad de avance, la distancia entre las líneas también aumenta. El grosor de la viruta es aproximadamente igual al avance.
Las velocidades de corte se publican en sfm porque la velocidad de corte ideal para una familia particular de herramientas será, en teoría, la misma sin importar el tamaño de la herramienta. Se espera que el ingeniero, el programador o el maquinista calculen las rpm necesarias para producir la velocidad de corte adecuada para cada herramienta seleccionada.
Entonces, ¿qué nos dice esto? Digamos que una herramienta de 1″ de diámetro debe funcionar a 100 sfm. Basándonos en la ecuación, esa herramienta debe girar a 382 rpm para conseguir 100 sfm: 100 ÷ 1 × 3,82 = 382.
Otra forma de considerar este concepto es pensar en la distancia que recorrería la herramienta de 1″ si realizara 382 revoluciones por el taller. En ese caso, viajaría 100′; si lo hace en 60 segundos, viajaría 100 sfm.
Las distancias son diferentes, por supuesto, porque la pieza de trabajo gira en lugar del cortador. Como la fórmula de la velocidad de corte depende del diámetro, a medida que el diámetro de la pieza disminuye, las rpm deben aumentar para mantener una velocidad superficial constante. Después de cada corte circular en el torno, el diámetro exterior de la pieza disminuye o el diámetro interior aumenta, y es necesario que las rpm de la pieza aumenten para mantener la velocidad de corte deseada. Por ello, los fabricantes de CNC han desarrollado la función de paso de superficie constante para los controles de los tornos. Esta función permite al programador introducir la velocidad de corte deseada en sfm o m/min. y el control calcula las rpm adecuadas para el diámetro cambiante.
Mientras la herramienta o la pieza está girando, la máquina debe saber a qué velocidad desplazarse mientras la fresa está engranada en la pieza. La velocidad de avance es el término que describe la velocidad de desplazamiento durante el corte.
La velocidad de avance para el fresado se suele expresar en pulgadas por minuto (ipm) y se calcula mediante: ipm = rpm × nº de canales × carga de viruta.
¿Qué es la carga de viruta? En el fresado, es la cantidad de material que el filo de corte elimina cada vez que gira. En el torneado, es la distancia que recorre la pieza en una revolución mientras está acoplada a la herramienta. A veces se denomina espesor de la viruta, lo que es más o menos cierto. El grosor de la viruta puede cambiar cuando cambian otros parámetros como el DOC radial o el ángulo de avance de la herramienta.
Los fabricantes de herramientas publican recomendaciones de carga de viruta junto con recomendaciones de velocidad de corte y las expresan en milésimas de pulgada (milímetros para unidades métricas). Para las operaciones de fresado y taladrado, la carga de viruta se expresa en milésimas de pulgada por flauta. Las flautas, los dientes y los filos de corte describen lo mismo y debe haber al menos uno, pero, en teoría, no hay límite en el número que puede tener una herramienta.
Las recomendaciones de carga de viruta para las operaciones de torneado se dan más a menudo en milésimas de pulgada por revolución, o avance por revolución. Esta es la distancia que la herramienta avanza cada vez que la pieza completa una rotación.
¿Qué rpm y velocidad de avance deberían programarse para una fresa de 4 filos, de 1″, que funciona a una velocidad de corte recomendada de 350 sfm y una carga de viruta recomendada de 0,005 pulgadas por diente (ipt)? Utilizando la ecuación, rpm = sfm ÷ diámetro × 3,82 = 350 ÷ 1,0 × 3,82 = 1.337, la velocidad de avance = rpm × nº de filos × carga de viruta = 1.337 × 4 × 0,005 = 26,74 ipm.
Aquí es donde las cosas se ponen interesantes, porque cambiando los valores en la fórmula, las relaciones de las diferentes variables se hacen evidentes. Prueba a aplicar una herramienta de 2″ en lugar de la de 1″. ¿Qué ocurre? Las revoluciones y el avance se reducen a la mitad.
Entender estas relaciones y aplicar un poco de pensamiento creativo puede proporcionar ganancias significativas en la eficiencia. En mi próxima columna hablaré de cómo aprovechar estas relaciones. CTE
Acerca del autor: Christopher Tate es ingeniero superior de fabricación avanzada de Milwaukee Electric Tool Corp. en Brookfield, Wisconsin. Tiene su sede en la planta de fabricación de la empresa en Jackson, Mississippi. Tiene 19 años de experiencia en la industria metalúrgica y tiene un máster en ciencias y una licenciatura en ciencias por la Universidad Estatal de Mississippi. Correo electrónico: [email protected].