Habiendo definido que, la función logarítmica y = log b x es la función inversa de la función exponencial y = b x. Ahora podemos proceder a graficar funciones logarítmicas viendo la relación entre las funciones exponenciales y logarítmicas.
Pero antes de entrar en el tema de la gráfica de funciones logarítmicas, es importante que nos familiaricemos con los siguientes términos:
- El dominio de una función
El dominio de una función es un conjunto de valores que puedes sustituir en la función para obtener una respuesta aceptable.
- El rango de una función
Es el conjunto de valores que se obtiene después de sustituir los valores del dominio por la variable.
- Asíntotas
Hay tres tipos de asíntotas, a saber; vertical, horizontal y oblicua. La asíntota vertical es el valor de x en el que la función crece sin límite cerca.
Las asíntotas horizontales son valores constantes a los que f(x) se aproxima a medida que x crece sin límite. Las asíntotas oblicuas son polinomios de primer grado a los que f(x) se acerca a medida que x crece sin límite.
¿Cómo se grafican las funciones logarítmicas?
La graficación de una función logarítmica se puede hacer examinando la gráfica de la función exponencial y luego intercambiando x e y.
La gráfica de una función exponencial f (x) = b x o y = b x contiene las siguientes características:
- El dominio de una función exponencial son los números reales (-infinito, infinito).
- El rango también son los números reales positivos (0, infinito)
- La gráfica de una función exponencial pasa normalmente por el punto (0, 1). Esto significa que la intersección y está en el punto (0, 1).
- La gráfica de una función exponencial f(x) = b x tiene una asíntota horizontal en y = 0.
- Una gráfica exponencial disminuye de izquierda a derecha si 0 < b < 1, y este caso se conoce como decaimiento exponencial.
- Si la base de la función f(x) = b x es mayor que 1, entonces su gráfica aumentará de izquierda a derecha y se llama crecimiento exponencial.
- Una función logarítmica tendrá como dominio (0, infinito).
- El rango de una función logarítmica es (-infinito, infinito).
- La gráfica de la función logarítmica pasa por el punto (1, 0), que es el inverso de (0, 1) para una función exponencial.
- La gráfica de una función logarítmica tiene una asíntota vertical en x = 0.
- La gráfica de una función logarítmica disminuirá de izquierda a derecha si 0 < b < 1.
- Y si la base de la función es mayor que 1, b > 1, entonces la gráfica aumentará de izquierda a derecha.
- Como todas las funciones logarítmicas pasan por el punto (1, 0), localizamos y colocamos un punto en el punto.
- Para evitar que la curva toque el eje y, dibujamos una asíntota en x = 0.
- Si la base de la función es mayor que 1, aumenta su curva de izquierda a derecha. Del mismo modo, si la base es menor que 1, disminuye la curva de izquierda a derecha.
- Obviamente, una función logarítmica debe tener el dominio y el rango de (0, infinito) y (-infinito, infinito)
- Dado que la función f(x) = log 2 x es mayor que 1, aumentaremos nuestra curva de izquierda a derecha, como se muestra a continuación.
- No podemos ver la asíntota vertical en x = 0 porque está oculta por el eje y.
- Coloca un punto en el punto (1, 0). Todas las curvas logarítmicas pasan por este punto.
- Dibuja una asíntota en x = 0.
- Como la base de la función y = log 5 x es menor que 1, decreceremos nuestra curva de izquierda a derecha.
- La función y = log 5 x también tendrá como dominio y rango (0, infinito) y (-infinito, infinito).
- El intercepto x se desplaza hacia la izquierda o la derecha una distancia fija igual a h.
- La asíntota vertical se desplaza una distancia igual a h.
- El dominio de la función también cambia.
- La intersección de x se moverá hacia arriba o hacia abajo con una distancia fija de k
Viendo las características anteriores de una en una, podemos deducir de forma similar las características de las funciones logarítmicas de la siguiente forma:
¿Cómo graficar una función logarítmica básica?
Una función logarítmica básica suele ser una función sin desplazamiento horizontal ni vertical.
Aquí tienes los pasos para crear una gráfica de una función logarítmica básica.
Ahora vamos a ver los siguientes ejemplos:
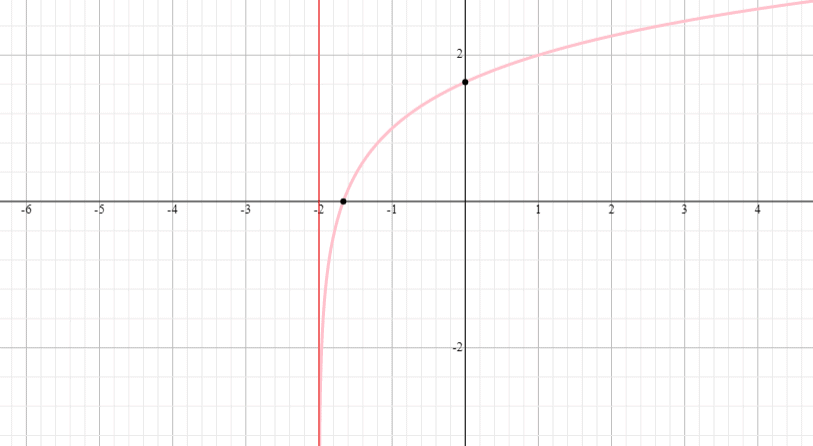
Ejemplo 1
Grafía la función logarítmica f(x) = log 2 x e indica el rango y el dominio de la función.
Solución
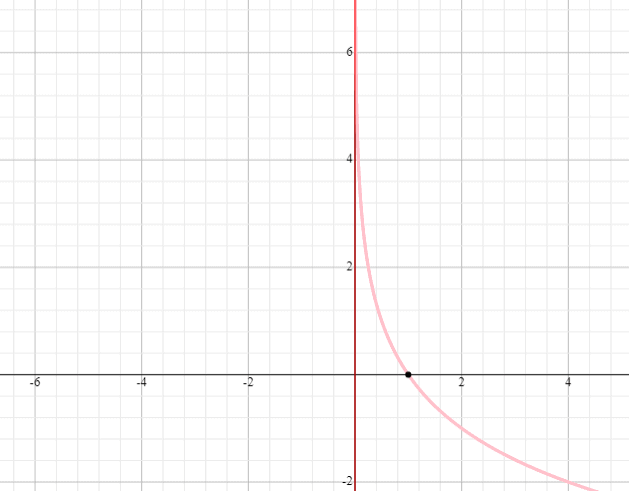
Ejemplo 2
Dibuja una gráfica de y = log 0,5 x
Solución
Grabación de una función logarítmica con desplazamiento horizontal
Las funciones logarítmicas con desplazamiento horizontal son de la forma f(x) = log b (x + h) o f (x) = log b (x – h), donde h = el desplazamiento horizontal. El signo del desplazamiento horizontal determina la dirección del desplazamiento. Si el signo es positivo, el desplazamiento será negativo, y si el signo es negativo, el desplazamiento se convierte en positivo.
Al aplicar el desplazamiento horizontal, las características de una función logarítmica se ven afectadas de las siguientes maneras:
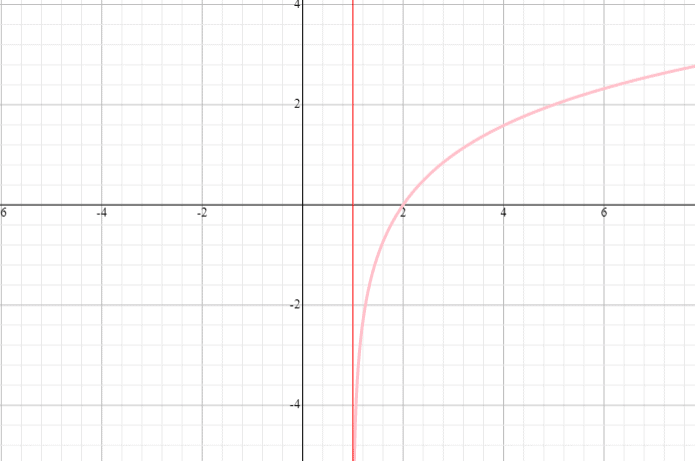
Ejemplo 3
Dibuja una gráfica de la función f(x) = log 2 (x + 1) e indica el dominio y el rango de la función.
Solución
⟹ Dominio: (- 1, infinito)
⟹ Rango: (-infinito, infinito)
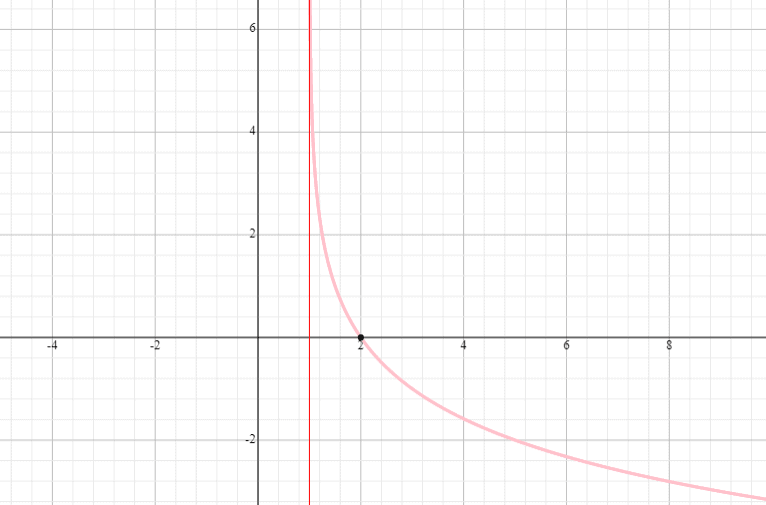
Ejemplo 4
Grafía y = log 0,5 (x – 1) y el estado el dominio y el rango.
Solución
⟹ Dominio: (1, infinito)
⟹ Rango: (-infinito, infinito)
¿Cómo graficar una función con una vertical?
Una función logarítmica con desplazamiento horizontal y vertical es de la forma f(x) = log b (x) + k, donde k = el desplazamiento vertical.
El desplazamiento vertical afecta a las características de una función de la siguiente manera:
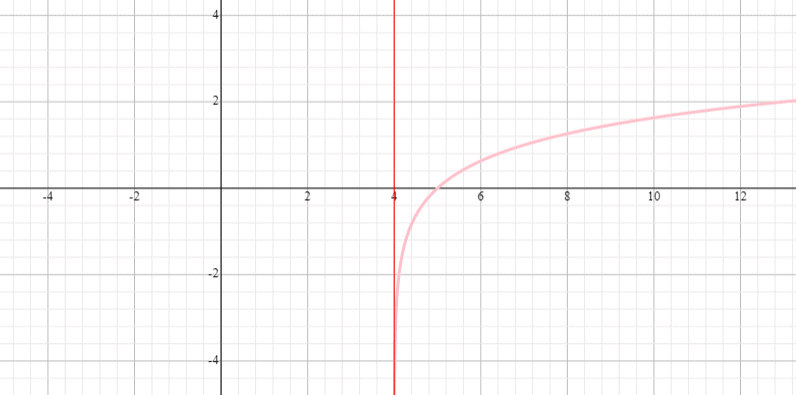
Ejemplo 5
Grafíe la función y = log 3 (x – 4) e indique el rango y el dominio de la función.
Solución
⟹ Dominio: (0, infinito)
⟹ Rango: (-infinito, infinito)
Funciones con desplazamiento horizontal y vertical
Una función logarítmica con desplazamiento horizontal y vertical es de la forma (x) = log b (x + h) + k, donde k y h son los desplazamientos vertical y horizontal, respectivamente.
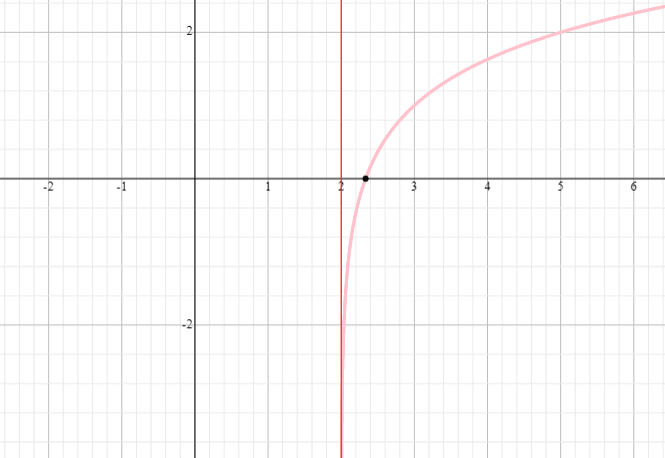
Ejemplo 6
Grafía la función logarítmica y = log 3 (x – 2) + 1 y encuentra el dominio y el rango de la función.
Solución
⟹ Dominio: (2,infinito)
⟹ Rango: (-infinito, infinito)
Ejemplo 7
Grafía la función logarítmica y = log 3 (x + 2) + 1 y encuentra el dominio y el rango de la función.
Solución
⟹ Dominio: (- 2,infinito)
⟹ Rango: (-infinito, infinito)