Regresión Probit
En la regresión Probit, la función de distribución normal acumulativa \(\Phi(\cdot)\) se utiliza para modelar la función de regresión cuando la variable dependiente es binaria, es decir, asumimos\/p>
(\beta_0 + \beta_1 X\) en (11.4) juega el papel de un cuantil \(z\). Recuerde que \ tal que el coeficiente Probit \(\beta_1\) en (11.4) es el cambio en \(z\) asociado con un cambio de una unidad en \(X\). Aunque el efecto sobre \(z\) de un cambio en \(X\) es lineal, el vínculo entre \(z\) y la variable dependiente \(Y\) es no lineal, ya que \(\Phi\) es una función no lineal de \(X\).
Dado que la variable dependiente es una función no lineal de los regresores, el coeficiente sobre \(X\) no tiene una interpretación sencilla. De acuerdo con el Concepto Clave 8.1, el cambio esperado en la probabilidad de que \(Y=1\) debido a un cambio en \(P/I \ ratio) puede calcularse como sigue:
- Calcule la probabilidad predicha de que \(Y=1\) para el valor original de \(X\).
- Calcule la probabilidad predicha de que \(Y=1\) para \(X + \Delta X\).
- Calcule la diferencia entre ambas probabilidades predichas.
-
Calcular \(z = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k\)
-
Buscar \(\Phi(z)\) llamando a pnorm().
Por supuesto, podemos generalizar (11.4) a la regresión Probit con múltiples regresores para mitigar el riesgo de enfrentarse al sesgo de las variables omitidas. Los fundamentos de la regresión Probit se resumen en el Concepto Clave 11.2.
Modelo Probit, Probabilidades Predichas y Efectos Estimados
Suponga que \N(Y\N) es una variable binaria. El modelo
es el modelo Probit poblacional con múltiples regresores \(X_1, X_2, \dots, X_k\) y \(\Phi(\cdot)\Nla función de distribución normal acumulada.
La probabilidad predicha de que \(Y=1\) dado \(X_1, X_2, \dots, X_k\) se puede calcular en dos pasos:
(\beta_j\) es el efecto sobre \(z\) de un cambio de una unidad en el regresor \(X_j\), manteniendo constantes todos los demás regresores \(k-1\).
El efecto sobre la probabilidad predicha de un cambio en un regresor puede calcularse como en el Concepto Clave 8.1.
En R, los modelos Probit pueden estimarse utilizando la función glm() del paquete stats. Utilizando el argumento family especificamos que queremos utilizar una función de enlace Probit.
# estimate the simple probit modeldenyprobit <- glm(deny ~ pirat, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Al igual que en el modelo de probabilidad lineal encontramos que la relación entre la probabilidad de denegación y el ratio pagos-ingresos es positiva y que el coeficiente correspondiente es altamente significativo.
El siguiente fragmento de código reproduce la Figura 11.2 del libro.
# plot dataplot(x = HMDA$pirat, y = HMDA$deny, main = "Probit Model of the Probability of Denial, Given P/I Ratio", xlab = "P/I ratio", ylab = "Deny", pch = 20, ylim = c(-0.4, 1.4), cex.main = 0.85)# add horizontal dashed lines and textabline(h = 1, lty = 2, col = "darkred")abline(h = 0, lty = 2, col = "darkred")text(2.5, 0.9, cex = 0.8, "Mortgage denied")text(2.5, -0.1, cex= 0.8, "Mortgage approved")# add estimated regression linex <- seq(0, 3, 0.01)y <- predict(denyprobit, list(pirat = x), type = "response")lines(x, y, lwd = 1.5, col = "steelblue")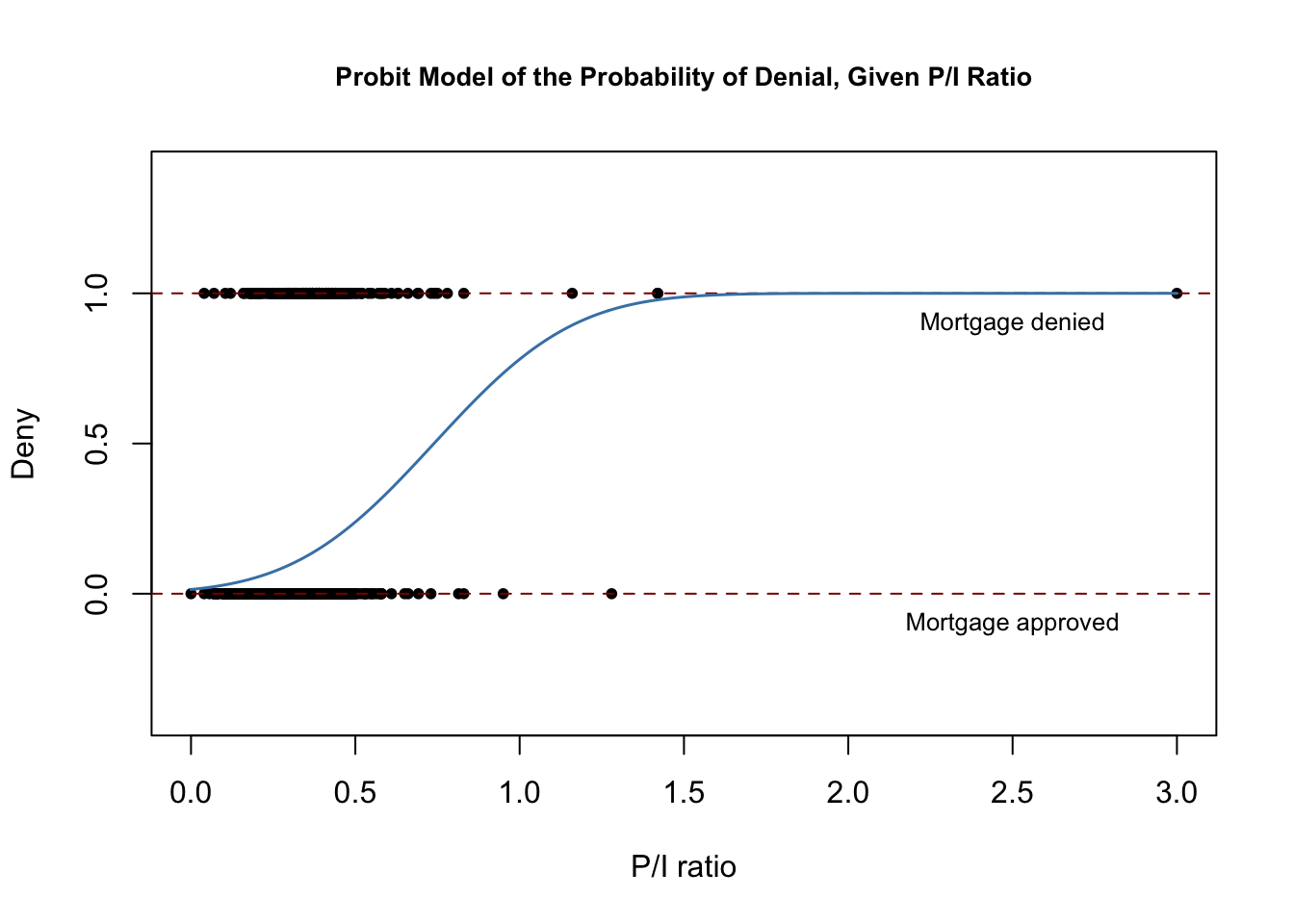
La función de regresión estimada tiene una forma de «S» estirada que es típica de la FCD de una variable aleatoria continua con PDF simétrica como la de una variable aleatoria normal. La función es claramente no lineal y se aplana para valores grandes y pequeños de \ (P/I \ ratio). La forma funcional también garantiza que las probabilidades condicionales predichas de una denegación se sitúan entre \(0\) y \(1\).
Utilizamos predict() para calcular el cambio predicho en la probabilidad de denegación cuando \(P/I \\\ ratio) se incrementa desde \(0.
# 1. compute predictions for P/I ratio = 0.3, 0.4predictions <- predict(denyprobit, newdata = data.frame("pirat" = c(0.3, 0.4)), type = "response")# 2. Compute difference in probabilitiesdiff(predictions)#> 2 #> 0.06081433Encontramos que un aumento en la relación pago-ingreso de \ (0,3) a \ (0,4) se predice que aumenta la probabilidad de denegación en aproximadamente \ (6.2\%\).
Continuamos utilizando un modelo Probit aumentado para estimar el efecto de la raza en la probabilidad de denegación de una solicitud de hipoteca.
denyprobit2 <- glm(deny ~ pirat + black, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La ecuación estimada del modelo es
Si bien todos los coeficientes son altamente significativos, tanto los coeficientes estimados de la relación pagos-ingresos como el indicador de ascendencia afroamericana son positivos. Una vez más, los coeficientes son difíciles de interpretar, pero indican que, en primer lugar, los afroamericanos tienen una mayor probabilidad de ser rechazados que los solicitantes blancos, manteniendo constante la relación pagos-ingresos y, en segundo lugar, los solicitantes con una alta relación pagos-ingresos se enfrentan a un mayor riesgo de ser rechazados.
¿Cuál es la diferencia estimada en las probabilidades de rechazo entre dos hipotéticos solicitantes con la misma relación pagos-ingresos? Al igual que antes, podemos utilizar predict() para calcular esta diferencia.
# 1. compute predictions for P/I ratio = 0.3predictions <- predict(denyprobit2, newdata = data.frame("black" = c("no", "yes"), "pirat" = c(0.3, 0.3)), type = "response")# 2. compute difference in probabilitiesdiff(predictions)#> 2 #> 0.1578117En este caso, la diferencia estimada en las probabilidades de denegación es de aproximadamente \N(15,8\%\).