La Regla de Cramer es otro método que puede resolver sistemas de ecuaciones lineales utilizando determinantes.
En cuanto a las notaciones, una matriz es una matriz de números encerrada entre corchetes mientras que el determinante es una matriz de números encerrada entre dos barras verticales.
Notaciones
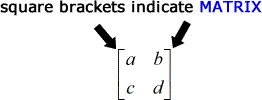
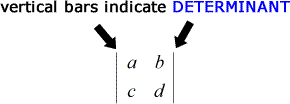
La fórmula para encontrar el determinante de una matriz de 2 x 2 es muy sencilla.
Hagamos un rápido repaso:
El determinante de una matriz de 2 x 2
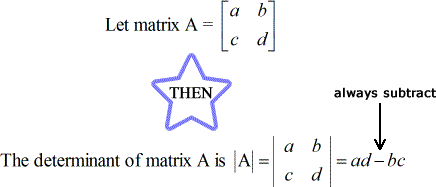
Ejemplos rápidos de cómo encontrar los determinantes de una matriz de 2 x 2
Ejemplo 1: Halla el determinante de la matriz A de abajo.
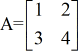
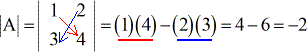
Ejemplo 2: Halla el determinante de la matriz B que aparece a continuación.
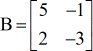
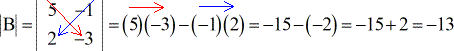
Ejemplo 3: Halla el determinante de la matriz C de abajo.
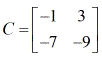
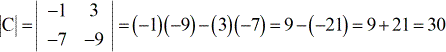
Después de saber cómo encontrar el determinante de una matriz de 2 x 2, ya estás preparado para aprender los procedimientos o pasos sobre cómo utilizar la Regla de Cramer. ¡Allá vamos!
Reglas de Cramer para sistemas de ecuaciones lineales con dos variables
- Dado un sistema lineal

- Asigna nombres para cada matriz
Matriz de coeficientes:
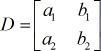
X – matriz:
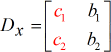
Y – matriz:
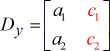
Para resolver la variable x.
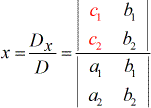
Para resolver la variable y.
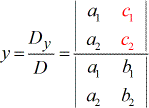
Pequeños puntos a tener en cuenta al ver la fórmula:
1) Las columnas de \large{x}, \large{y}, y los términos constantes \large{c} se obtienen de la siguiente manera:
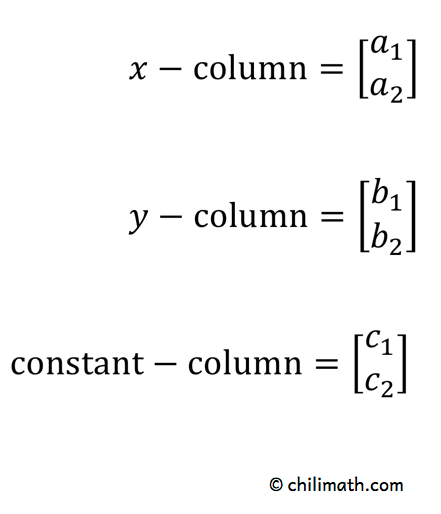
2) Ambos denominadores en la resolución de \large{x} y \large{y} son iguales. Provienen de las columnas de \large{x} y \large{y}.
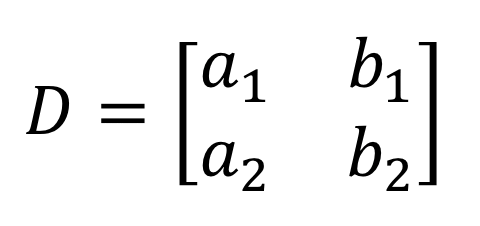
3) Observando el numerador en la resolución de \large{x}, los coeficientes de la columna \large{x} se sustituyen por la columna de la constante (en rojo).
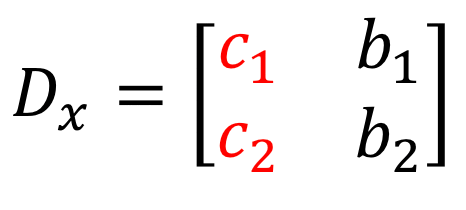
4) De la misma manera, para resolver para \large{y}, se sustituyen los coeficientes de \large{y}-columna por la columna constante (en rojo).
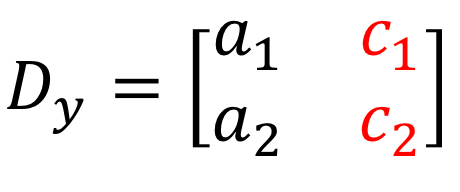
Ejemplos de cómo Resolver sistemas de ecuaciones lineales con dos variables utilizando la regla de Cramer
Ejemplo 1: Resuelve el sistema con dos variables por la Regla de Cramer
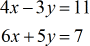
Comienza extrayendo las tres matrices relevantes: coeficiente, \large{x}, y \large{y}. A continuación, resolver cada uno de los determinantes correspondientes.
- Para la matriz de coeficientes
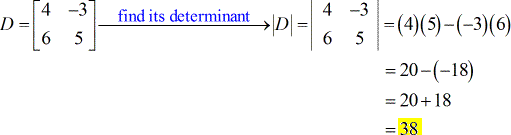
- Para la matriz X

- Para la matriz Y –

Una vez calculados los tres determinantes, es el momento de resolver los valores de \large{x} y \large{y} utilizando la fórmula anterior.
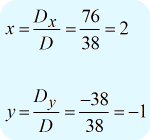
Puedo escribir la respuesta final como \large( {x,y} \right) = \left( {2, – 1} \right)}.
Ejemplo 2: Resolver el sistema con dos variables por la regla de Cramer
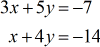
Configurar sus matrices de coeficientes, \large{x}, y \large{y} a partir del sistema de ecuaciones lineales dado. A continuación, calcula sus determinantes en consecuencia.
Recuerda que siempre restamos los productos de las entradas diagonales.
- Para la matriz de coeficientes (utiliza los coeficientes de las variables x e y)
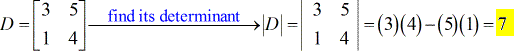
- Para la matriz X – (sustituir la columna x por la columna constante)
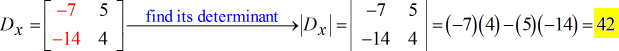
- Para la matriz Y – (sustituir la columna y por la columna constante)
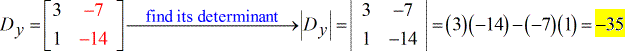
Espero que te estés sintiendo cómodo calculando el determinante de una matriz bidimensional. Para resolver finalmente las variables requeridas, obtengo los siguientes resultados…
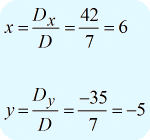
Escribiendo la respuesta final en notación de puntos, he obtenido \left( {x,y} \right) = \left( {6, – 5} \right)}.
Ejemplo 3: Resolver el sistema con dos variables por la Regla de Cramer
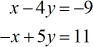
Este problema se puede resolver realmente con bastante facilidad por el Método de Eliminación. Esto se debe a que los coeficientes de la variable x son los «mismos» pero sólo de signos opuestos ( +1 y -1 ). Para resolverlo mediante el método de eliminación, se suman sus correspondientes columnas y la variable x desaparece – dejándote con una ecuación de un solo paso en \large{y}. Menciono esto porque cada técnica tiene defectos y es mejor elegir la más eficiente. Aclara siempre con tu profesor si está bien utilizar otro enfoque cuando el método no está especificado en un problema determinado.
De todas formas, ya que estamos aprendiendo a resolver por la Regla de Cramer, vamos a trabajar con este método.
Construiré tres matrices ( coeficiente, \large{x} y \large{y}) y evaluaré sus correspondientes determinantes.
- Para la matriz coeficiente
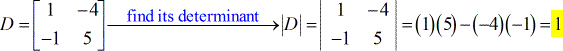
- Para la matriz X – ( escrita como D en mayúsculas con subíndice x )
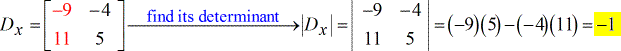
- Para la matriz Y – (escrita como D mayúscula con el subíndice y)
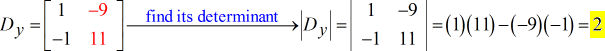
Después de obtener los valores de los tres determinantes requeridos, calcularé |grande{x} y |grande{y} como sigue.
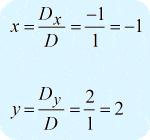
La respuesta final en la forma puntual es \large{left( {x,y} \right) = \left( { – 1,2} \right)} .
Ejemplo 4: Resuelve por la Regla de Cramer el sistema con dos variables
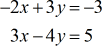
Como ya hemos repasado algunos ejemplos, te sugiero que intentes este problema por tu cuenta. Luego, compara tus respuestas con la solución que aparece a continuación.
Si lo consigues a la primera significa que te estás convirtiendo en un «profesional» con respecto a la Regla de Cramer. Si no lo hiciste, trata de averiguar qué fue lo que falló y aprende a no cometer el mismo error la próxima vez. Así es como te vuelves mejor en matemáticas. Estudia muchos tipos de problemas y, lo que es más importante, haz mucha práctica independiente.
- Para la matriz de coeficientes
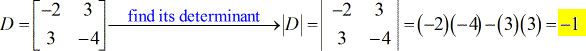
- Para la matriz X
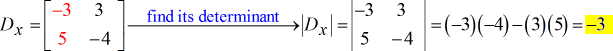
- Para la matriz Y –
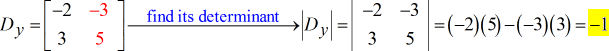
Deberías obtener la respuesta a continuación…
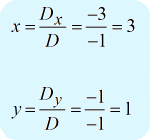
Ejemplo 5: Resolver el sistema con dos variables por la regla de Cramer
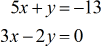
Para nuestro último ejemplo, he incluido un cero en la columna de la constante. Cada vez que veas el número cero en la columna de la constante, te recomiendo encarecidamente que utilices la Regla de Cramer para resolver el sistema de ecuaciones lineales. ¿Por qué? Porque el cálculo de los determinantes para las matrices \ge{x} y \ge{y} se convierte drásticamente en súper fácil. ¡Compruébalo tú mismo!
- Para la matriz de coeficientes
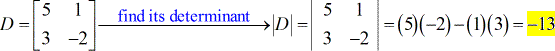
- Para la matriz X
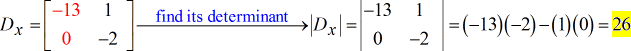
- Para la matriz Y
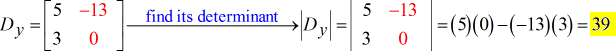
La solución final de este problema es
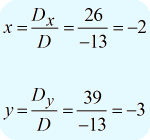
Práctica con hojas de trabajo
También te puede interesar:
Regla de Camer 3×3