Calcular la Impedancia
En los circuitos de corriente alterna, la Ley de Ohm toma la forma más general: E = I⋅Z, donde E es la tensión e I es la corriente, como antes. El nuevo término, Z, es la impedancia, una combinación vectorial de:
- Resistencia, R (en ohmios), con caídas de tensión en fase con la corriente.
- Reactancia inductiva, XL (en ohmios), con caídas de tensión que adelantan a la corriente en 90°.
- Reactancia capacitiva, XC (en ohmios) con gotas de tensión que van por detrás de la corriente en 90°.
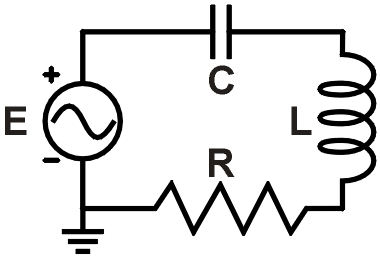
f = 6,4 kHz R = 120 Ω
L = 3,6 mH C = 0,38 μf
Figura 1. Ejemplo de circuito RLC

Figura 2. La suma vectorial de R y
XL-XC da como resultado Z
A partir de las fórmulas para XL y XC, se puede ver que las reactancias dependen tanto de los valores de los componentes L y C, como de la frecuencia de CA, f:
![]() y
y 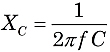
Donde f es la frecuencia enHertz (o seg-1), L es la inductancia en Henries, y C es la capacitancia en faradios. Debido a que XL y X tienen una diferencia de fase de 180°, la reactancia total X de un circuito en serie es XL-XC.
Los usos conocidos de la Ley de Ohm, como los cálculos de circuitos en serie y en paralelo, siguen siendo válidos. Sin embargo, ahora debe considerar las contribuciones vectoriales en competencia de las resistencias y reactancias.
Ángulos de fase y vectores
Hallemos la impedancia total del circuito de la figura 1. Utilizando las fórmulasanteriores:
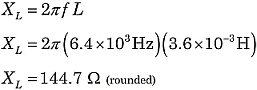 |
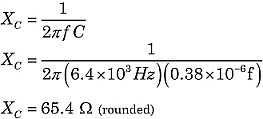 |
Construyendo la impedancia Z, la resistencia contribuye a la componente horizontal. La componente vertical es la diferencia de las reactancias: XL-XC.Entonces, Z es la suma vectorial de R y XL-XC,como se ilustra en la Figura 2.
En la Figura 2, viendo que Z es la hipotenusa de un triángulo rectángulo, podemos utilizar el teorema de Pitágoras y la geometría del triángulo rectángulo para evaluar Z.
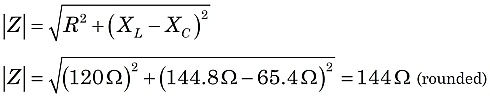
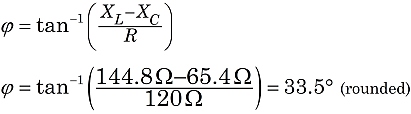
Así, en este circuito, seríamos testigos del efecto de una impedancia de144 ohmios, con la corriente retrasada respecto a la tensión de alimentación con un ángulo de fase de 33.5°.
Como se puede adivinar de la discusión anterior, es muy posible que las reactancias inductivas y capacitivas se cancelen exactamente bajo las combinaciones correctas de L, C, y los valores de f. Esta es una condición muy importante conocida como resonancia.