Wprowadzenie
Właściwości plastyczne odgrywają ważną rolę w wielu procesach membranowych, takich jak na przykład fuzja membran (Chernomordik i Kozlov, 2008) i modulacje aktywności kanałów membranowych (Schmidt i MacKinnon, 2008; Sansom i Biggin, 2010; Mashaghi i in., 2013b). W komórkach, błony zewnętrzne są podtrzymywane przez leżące u ich podłoża sieci aktyny. Naprężenia mechaniczne są wówczas zdominowane przez związany z nimi cytoszkielet aktynowy w skalach długości większych niż rozmiar oczek sieci aktynowej (30-300 nm) (Morone i in., 2006). Na małych skalach długości, jednakże, udział dwuwarstwy lipidowej będzie dominujący. W związku z tym, podjęto wysiłki w celu zbadania właściwości mechanicznych płatów dwuwarstwowych o wymiarach zbliżonych do rozmiaru oczek sieci aktynowej (Claesson i in., 2011).
Rozważając membranę jako ciało dwuwymiarowe, tj. zaniedbując jej grubość, jej właściwości mechaniczne przy braku anizotropii mogą być scharakteryzowane przez dwie stałe sprężystości zgodnie z teorią sprężystości continuum. W powszechnej praktyce charakteryzacji materiałów, parametrami tymi są zwykle moduł Younga i współczynnik Poissona. Oszacowanie modułu Younga dla membran zostało dostarczone przez eksperymenty (Tierney et al., 2005; Popescu et al., 2006). Jednakże, pomiar współczynnika Poissona nie jest prosty, ze względu na małą grubość membran w zakresie nanometrów (Mitchell et al., 2003; Martins et al., 2009). Z teoretycznego punktu widzenia, właściwości mechaniczne membran lipidowych są powszechnie badane w oparciu o Hamiltonian Helfricha. Główną wielkością fizyczną uzyskiwaną w takich badaniach jest sztywność zginania. Moduł Younga i współczynnik Poissona są wzajemnie powiązane poprzez wzory uwzględniające sztywność zginania, ale jak dotąd ani moduł Younga ani współczynnik Poissona nie zostały wyznaczone oddzielnie.
Symulacje i modele teoretyczne zostały wykorzystane do dostarczenia ważnych informacji na temat sprężystych (Goetz i Lipowsky, 1998; Lindahl i Edholm, 2001; Ayton i in., 2002) i lepkich właściwości dwuwarstw lipidowych (Jeon i Voth, 2005). Badanie właściwości mechanicznych cienkich warstw nie ogranicza się do biomembran i stanowi aktywny obszar badań w naukach materiałowych. Podjęto wysiłki w celu przewidzenia współczynnika Poissona folii wykonanych z różnych materiałów za pomocą symulacji komputerowych. Na przykład Galvao et al. zastosowali symulacje dynamiki molekularnej z wykorzystaniem reaktywnych empirycznych potencjałów rzędu wiązań w celu zbadania właściwości mechanicznych nanowłókien grafenowych (Martins i Galvao, 2010). Baughman i in. zaproponowali model szacowania współczynnika Poissona sieci włókien i z powodzeniem zastosowali go do arkuszy nanorurek węglowych (buckypaper) (Hall i in., 2008).
W niniejszej pracy przedstawiamy metodę wyznaczania współczynnika Poissona ν w symulacjach i stosujemy ją do modelu gruboziarnistej błony lipidowej, który został wprowadzony przez Lenza i Schmida (2005). Metoda ta jest ogólna i można ją stosować do dowolnych innych powierzchni. Po wyznaczeniu sztywności zginania kc ze spektrum mocy fluktuacji wysokości membrany, jesteśmy w stanie obliczyć moduł Younga E.
Materiały i Metody
Symulacje Monte Carlo dwuwarstw lipidowych z periodycznymi warunkami brzegowymi w kierunkach bocznych przeprowadzono dla gruboziarnistego modelu wprowadzonego przez Lenza i Schmida (2005). W modelu tym rozważane są amfifile jednoogonowe, które reprezentowane są przez sześć kulek ogonowych i jedną nieco większą kulkę głowową (o stosunku rozmiarów 1-1.1). Kulki należące do jednej molekuły są połączone za pomocą sprężyn o skończonej rozciągliwości nieliniowej (FENE) (Grest i Kremer, 1986) z potencjałem rozciągającym wiązania Rysunek 1:
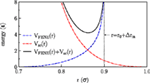
Rysunek 1. Oddziaływania zastosowane w modelu.
Tutaj r jest odległością między sąsiednimi kulkami, νFENE charakteryzuje siłę sprężyny, r0 jest optymalną długością wiązania (brak rozciągania), a Δrm jest maksymalną odległością rozciągania. Sztywność ogonów jest uwzględniana przez harmoniczny potencjał kąta wiązania
gdzie θijk jest kątem wiązania związanym z trzema sąsiednimi koralikami. Zarówno niezwiązane kulki należące do tej samej cząsteczki, jak i kulki należące do różnych cząsteczek oddziałują poprzez potencjał miękkiego rdzenia:
gdzie θ(.) jest funkcją stopnia Heaviside’a. Cząsteczki rozpuszczalnika są reprezentowane przez fantomowy model kulek, które oddziałują z kulkami lipidowymi poprzez VSC(r) (z tymi samymi parametrami co kulki głowowe), ale nie oddziałują ze sobą. Wszystkie parametry modelu zostały dobrane zgodnie z modelem referencyjnym (Lenz i Schmid, 2005) i są zestawione w tabeli 1.

Tabela 1. Potencjały interakcyjne modelu referencyjnego i odpowiadające im parametry.
Bliźniaki lipidowe wykazują bogate spektrum struktur i przejść fazowych (Nagle i Tristram-Nagle, 2000; Illya i in., 2005; Seto i in., 2008; Thakkar i in., 2011). Stan płynny w wysokich temperaturach charakteryzuje się nieuporządkowanym układem ogonów lipidowych i stosunkowo dużą ruchliwością lipidów. Po ochłodzeniu, stan płynny przechodzi w stan żelu, w którym cząsteczki lipidów są bardziej uporządkowane i mają mniejszą ruchliwość. Inne możliwe fazy to faza interdygitacji, w której ogony lipidowe z przeciwległych monowarstw przenikają się nawzajem.
Skanując diagram fazowy modelu (Lenz, 2007), najpierw zrównaliśmy bilayery lipidowe przez około dwa miliony kroków Monte Carlo (MC), aby uzyskać różne fazy dla celów tej pracy, patrz rysunek 2. W zredukowanych jednostkach, ϵ/kB dla temperatury T i ϵ/σLJ3 dla ciśnienia P, odpowiadające im zmienne termodynamiczne to: P = 2 i T = 1,08 dla fazy żelowej, P = 1 i T = 1,3 dla fazy płynnej, P = 0,5 i T = 1,16 dla fazy międzywęzłowej. Charakterystyczne parametry dla poszczególnych faz, w tym średnią długość łańcucha l¯, grubość warstwy d, powierzchnię przypadającą na lipid A oraz parametr uporządkowania łańcucha Sz zestawiono w tabeli 2.

Figura 2. Migawki symulowanej membrany lipidowej w fazie (A) żelu, (B) płynu i (C) interdygitalizacji. Koraliki główki lipidu i koraliki ogona pokazano odpowiednio na czerwono i zielono.
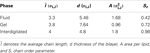
Tabela 2. Parametry charakterystyczne bilayerów lipidowych.
Symulacje przeprowadzono w warunkach stałej temperatury i ciśnienia (zespół NPT) dla bilayerów lipidowych o różnych rozmiarach. Aby zbadać spektrum mocy fluktuacji wysokości powierzchni, symulowano warstwę, której górny i dolny płat składa się z 64 × 64 cząsteczek lipidów. Do modelu rozpuszczalnika wybrano około 17000-72000 kulek (dokładna liczba zależy od symulowanej fazy). Aby przeprowadzić analizę współczynnika Poissona, zrównoważyliśmy prostokątne dwuwarstwy składające się z 12 × 24 cząsteczek lipidów na listek do trzech różnych faz.
Aby wyznaczyć zarówno E jak i ν, musimy wyznaczyć jedną z tych stałych sprężystości oddzielnie. Wykorzystując periodyczne warunki brzegowe, wprowadzamy metodę obliczania współczynnika Poissona dla powierzchni (Abedpour et al., 2010). Stosunek Poissona to ujemny stosunek zmian odkształcenia poprzecznego podzielony przez zmiany odkształcenia osiowego w ciele, gdy jest ono rozciągane lub ściskane wzdłuż kierunku osiowego pod wpływem naprężenia poniżej granicy proporcjonalności. Dla nieskończenie małych odkształceń skośnych, współczynnik Poissona można zastąpić stosunkiem względnych zmian długości jako νij = -ΔLi/ηjLi, gdzie ηj ≡ ΔLj/Lj jest zdefiniowane jako ułamek zmiany długości osiowej. W prezentowanej metodzie długość pomiędzy sąsiednimi lipidami jest przeskalowywana o współczynnik (1 + η) w kierunku osiowym, powiedzmy w kierunku y, a następnie monitorowana jest zmiana rozmiaru pudełka symulacyjnego w kierunkach prostopadłych, w tym przypadku w kierunku x i z. Przy zachowaniu stałej długości pudełka (1 + η) Ly, dla ustalenia ciśnienia w symulacjach, wymiary pudełka mogą się teraz zmieniać tylko w kierunku x i z. Gdy początkowe średnie długości w kierunku x i z wynosiły Lx i Lz, nowe średnie wartości Lx + ΔLx i Lz + ΔLz są osiągane po przeskalowaniu, poprzez ponowną ekwilibrację układu przez kilka kroków MC, patrz Rysunek 3.

Rysunek 3. Migawki błony lipidowej w fazie ciekłej jako (A) konfiguracja początkowa, (B) po zwiększeniu rozmiaru warstwy w kierunku y o współczynnik (1 + η) oraz (C) zrelaksowana warstwa ustalająca rozmiar błony w kierunku y i zmienna w kierunku x. W wyniku dodatniego współczynnika Poissona dla tej fazy, rozmiar membrany w kierunku x zmniejsza się i wyrównuje po kilku krokach MC. Główki i ogonki lipidów są zaznaczone odpowiednio na czerwono i zielono.
Podczas symulacji, aby przyspieszyć procedurę termalizacji po rozszerzeniu pudełka wzdłuż kierunku osiowego, nieznacznie podnieśliśmy temperaturę w układzie, co spowodowało zwiększenie ruchliwości cząsteczek. Dla fazy ciekłej ustawiliśmy temperaturę początkową na T = 1.3, a następnie zmieniliśmy ją na T = 1.4 na około dodatkowe 400 kroków, po czym wróciliśmy do pierwotnej wartości. Podobnie, dla fazy żelowej i międzywęzłowej, temperatury początkowe wynosiły T = 1.08 i T = 1.16 i zostały zmienione na T = 1.2 i T = 1.3, odpowiednio.
Powszechna analiza właściwości sprężystych membrany opiera się na Hamiltonianie Helfricha (Helfrich, 1973), który opisuje koszt sprężystej entalpii swobodnej związanej z fluktuacjami wysokości membrany (odchylenia od płaskiej powierzchni). Przy parametryzacji membrany we współrzędnych kartezjańskich (x,y) →(x,y,h(x,y)) (Monge gauge), hamiltonian Helfricha jest, dla małych fluktuacji, dany przez
gdzie kc jest sztywnością zginania, a σ napięciem powierzchniowym. Równanie (4) jest stosowane, gdy membrana jest traktowana jako ciało o zerowej grubości. Uogólniona teoria sprężystości dla membran o skończonej grubości została zaproponowana przez Brannigana i Browna (2006) i zastosowana do modelu Lenza-Schmida ostatnio (West i in., 2009; Neder i in., Aby wyznaczyć h(x, y) na podstawie symulacji, zdyskretyzowaliśmy płaszczyznę (x, y) na regularną siatkę o rozstawie 2σLJ, wyznaczyliśmy w każdej komórce (i, j) średnie współrzędne z+(i, j) i z-(i, j) główki paciorka odpowiednio w górnym i dolnym płatku i obliczyliśmy wysokość h(i, j) – /2 (średnia h¯ została następnie odjęta). Dla membrany o rozmiarach poprzecznych L × L, Eq. (4) przewiduje:
dla widma mocy fluktuacji, gdzie ĥ(q) jest transformatą Fouriera h(x, y) przy wektorze fali q, q = |q|, a <> oznacza średnią równowagową. W numerologii, ĥ(q) jest obliczana z dyskretnej transformaty Fouriera h(i, j). Jest oczywiste, że równanie (5) może być prawdziwe tylko dla zakresu q 2π/L ≪ q ≪ 2π/σLJ, gdzie ani skończony rozmiar układu, ani (atomistyczny) rozmiar perełek nie wpływa na fluktuacje. Odpowiedni zakres q dla układów o rozsądnych rozmiarach nie jest niestety duży, ale dopasowania < |ĥ(q)|2 > ∕kBTL2 w funkcji q2 w zakresie 0.5 ≤ q2 ≤ 1 dają dobrą zgodność z Eq. (5) dla naszych wielkości.
Wyniki i dyskusja
W tabeli 3 zestawiono uzyskane współczynniki Poissona νyx, νzx, i νxy oraz νzy dla różnych faz. Jak pokazano na rysunku 4, uzyskany w ten sposób współczynnik Poissona jest niezależny od współczynnika przeskalowania η, o ile η nie jest ani zbyt duży, co prowadzi do zniszczenia struktury membrany, ani zbyt mały, co nie zapewnia wystarczającej ilości wolnej przestrzeni dla ruchu cząstek. Zgodnie z tabelą 3 i rysunkiem 4, fazy płynna i międzywęzłowa mają taki sam zmierzony współczynnik Poissona zarówno dla kierunku x, jak i y. Oznacza to, że te dwie fazy są wzajemnie powiązane. Oznacza to, że te dwie fazy są izotropowe w płaszczyźnie dwuwarstwy. Nie dotyczy to już jednak fazy żelowej. Pomiary pokazują, że bilayer w fazie żelowej zachowuje się jak materiał anizotropowy, który ma dwie rozróżnialnie różne wartości dla dwóch różnych kierunków w płaszczyźnie bilayer’u.

Tabela 3. Stałe sprężyste uzyskane z symulacji membran lipidowych w różnych fazach.

Rysunek 4. Relaksacja -ΔLi/ηjLi w (A) cieczy, (B) interdygitacji i (C) fazie żelowej. Wartość plateau osiągana po około 5000 krokach MC, niezależna od wartości η, daje współczynnik Poissona ν. W fazie żelowej, współczynnik Poissona ma różne wartości dla νxy i νyx i faza ta działa jak powierzchnia anizotropowa.
Odwrotnie, gdy bilayer był rozszerzany w kierunku prostopadłym do płaszczyzny nachylenia, lipidy reorganizowały się w taki sposób, że bilayer kurczył się poprzecznie. W niniejszej pracy długości wiązań lipidów w kierunku z (prostopadłym do płaszczyzny dwuwarstwy) nie zostały przeskalowane. Wynika to z faktu, że aby zaobserwować efekt Poissona, długość pomiędzy kulkami powinna być przeskalowana o czynnik, który daje wystarczającą przestrzeń dla cząsteczek do rearanżacji. Jednak w kierunku z, wzrost ten powinien wystąpić pomiędzy związanymi kulkami wewnątrz lipidu, co powoduje rozerwanie wiązania. Podane wartości νzx i νzy są wynikowymi względnymi zmianami średniej długości dwuwarstwy spowodowanymi bocznym wydłużeniem dwuwarstwy odpowiednio w kierunku x i y.
Wartości uzyskane dla sztywności zginania kc wynoszą 5,2ϵ dla fazy płynnej i 7,6ϵ dla fazy międzywarstwowej. Dla fazy żelowej i płynnej, wyniki zgadzają się z wcześniejszymi raportami obliczeniowymi (West, 2008; West et al., 2009) oraz wynikami eksperymentalnymi (Falcioni et al., 1997; Liu and Zhang, 2009). Gęstość spektralna dla fazy międzywęzłowej została obliczona według tej samej metody. W tym miejscu podajemy sztywność zginania dla fazy międzywęzłowej. Rysunek 5 ilustruje widma fluktuacji wysokości dla trzech badanych faz i dopasowania do równania Eq. (5).
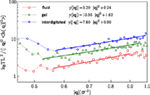
Rysunek 5. Widma fluktuacji dla fazy płynnej, żelowej i międzywęzłowej oraz dopasowania do równania Eq. (5).
W ramach dwuwymiarowej teorii sprężystości, sztywność zginania kc jest związana ze współczynnikiem Poissona ν i modułem Younga E zgodnie z (Landau i in., 1986)
gdzie d jest średnią grubością membrany, dla której otrzymujemy, 5.48σLJ, i 4.86σLJ odpowiednio dla cieczy i faz międzywęzłowych. Podstawiając założone wartości współczynników Poissona i sztywności zginania dla bilayerów w dwóch izotropowych fazach do równania (6), można otrzymać odpowiednie moduły Younga. Obliczone w ten sposób moduły Younga wynoszą 0,28 i 0,67 w jednostkach ϵ/σ3 odpowiednio dla stanu płynnego i międzywarstwowego. Oczywiście, obserwowana anizotropowość w fazie żelowej nie pozwala na zastosowanie powyższego twierdzenia dla dwuwarstwy w tej fazie.
Podejście przedstawione w tym artykule może być zastosowane do membran o bardziej złożonym składzie lipidów, biorąc pod uwagę, że istnieją dla nich zweryfikowane doświadczalnie modele oddziaływań. Podejście to może być również połączone z dokładniejszą symulacją bilayerów. W pełni atomistyczne symulacje, a w szczególności symulacje ab initio, mogłyby w zasadzie dostarczyć dokładniejszych opisów systemu, ale wiąże się to z ogromnym obciążeniem obliczeniowym (Mashaghi et al., 2012, 2013a).
Wniosek
Wykonaliśmy symulacje Monte Carlo gruboziarnistego modelu dwuwarstwy lipidowej, aby uzyskać wgląd w mechaniczne właściwości planarnych membran lipidowych. Dzięki zastosowaniu metody przeskalowania, mogliśmy wyznaczyć współczynnik Poissona ν dla różnych faz, oprócz sztywności zginania wyznaczonej z analizy fluktuacji wysokości membrany w oparciu o Hamiltonian Helfricha. Pozwala to również na obliczenie modułu Younga E dla różnych faz. Metoda ta jest dokładna, łatwa w implementacji i może być zastosowana do innych membran, takich jak grafen (Abedpour et al., 2010), w celu przewidzenia temperaturowej zależności współczynnika Poissona i modułu Younga. Innymi interesującymi systemami do badań są krystaliczne nanodruty metaliczne, których moduł sprężystości kontroluje ich strukturalną wydajność i funkcjonalne zachowanie, takie jak ich częstotliwość rezonansowa pod obciążeniem oscylacyjnym typowo stosowanym podczas uruchamiania i wykrywania (Chen et al., 2006; McDowell et al., 2008).
Oświadczenie o konflikcie interesów
Autorzy deklarują, że badania zostały przeprowadzone przy braku jakichkolwiek komercyjnych lub finansowych powiązań, które mogłyby być interpretowane jako potencjalny konflikt interesów.
Podziękowania
Chcielibyśmy podziękować Philippowi Maassowi za jego pomocne dyskusje.
Abedpour, N., Asgari, R., and Tabar, M. R. R. (2010). Nieodwracalność w odpowiedzi na siły działające na arkusze grafenowe. Phys. Rev. Lett. 104, 196804. doi:10.1103/PhysRevLett.104.196804
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Ayton, G., Smondyrev, A., Bardenhagen, S., McMurtry, P., and Voth, G. (2002). Calculating the bulk modulus for a lipid bilayer with nonequilibrium molecular dynamics simulation. Biophys. J. 82, 1226-1238. doi:10.1016/S0006-3495(02)75479-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Brannigan, G., and Brown, F. L. H. (2006). A consistent model for thermal fluctuations and protein induced deformations in lipid bilayers. Biophys. J. 90, 1501. doi:10.1529/biophysj.105.075838
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chen, C., Shi, Y., Zhang, Y., Zhu, J., and Yan, Y. (2006). Size dependence of Young’s modulus in ZnO nanowires. Phys. Rev. Lett. 96, 075505. doi:10.1103/PhysRevLett.96.075505
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chernomordik, L. V., and Kozlov, M. M. (2008). Mechanics of membrane fusion. Nat. Struct. Mol. Biol. 15, 675-683. doi:10.1038/nsmb.1455
CrossRef Full Text
Claesson, M., Frost, R., Svedhem, S., and Andersson, M. (2011). Pore spanning lipid bilayers on mesoporous silica having varying pore size. Langmuir 27, 8974-8982. doi:10.1021/la201411b
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Falcioni, M., Bowick, M. J., Guitter, E., and Thorleifsson, G. (1997). The Poisson ratio of crystalline surfaces. Europhys. Lett. 38, 67-72. doi:10.1016/j.jhazmat.2010.12.101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Goetz, R., and Lipowsky, R. (1998). Computer simulations of bilayer membranes: self-assembly and interfacial tension. J. Chem. Phys. 108, 7397-7409. doi:10.1063/1.476160
CrossRef Full Text
Grest, G. S., and Kremer, K. (1986). Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 33, 3628-3631. doi:10.1103/PhysRevA.33.3628
CrossRef Full Text
Hall, L., Coluci, V., Galvao, D., Kozlov, M., Zhang, M., Dantas, S., et al. (2008). Sign change of Poisson’s ratio for carbon nanotube sheets. Science 320, 504-507. doi:10.1126/science.1149815
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Helfrich, W. (1973). Właściwości sprężyste dwuwarstw lipidowych-teoria i możliwe eksperymenty. Z. Naturforsch. C 28, 693.
Illya, G., Lipowsky, R., and Shillcock, J. C. (2005). Effect of chain length and asymmetry on material properties of bilayer membranes. J. Chem. Phys. 122, 1-6. doi:10.1063/1.1917794
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Jeon, J., and Voth, G. (2005). The dynamic stress responses to area change in planar lipid bilayer membranes. Biophys. J. 88, 1104-1119. doi:10.1529/biophysj.104.052183
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Landau, L. D., Pitaevskii, L. P., Lifshitz, E. M., and Kosevich, A. M. (1986). Theory of Elasticity, Volume 7, 3rd Edn. Oxford: Butterworth-Heinemann.
Lenz, O. (2007). Symulacja komputerowa dwuwarstw lipidowych. Ph.D. thesis, University of Bielefeld, Bielefeld.
Lenz, O., and Schmid, F. (2005). A simple computer model for liquid lipid bilayers. J. Mol. Liq. 117, 147-152. doi:10.1016/j.molliq.2004.08.008
CrossRef Full Text
Lindahl, E., and Edholm, O. (2001). Molecular dynamics simulation of NMR relaxation rates and slow dynamics in lipid bilayers. J. Chem. Phys. 115, 4938-4950. doi:10.1529/biophysj.107.121806
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Liu, P., and Zhang, Y. W. (2009). Temperature-dependent bending rigidity of graphene. Appl. Phys. Lett. 94, 231912. doi:10.1063/1.3155197
CrossRef Full Text
Martins, B., and Galvao, D. (2010). Curved graphene nanoribbons: struktura i dynamika nanobeltów węglowych. Nanotechnology 21, 075710. doi:10.1088/0957-4484/21/7/075710
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Martins, P., Malhaire, C., Brida, S., and Barbier, D. (2009). On the determination of Poisson’s ratio of stressed monolayer and bilayer submicron thick films. Microsyst. Technol. 15, 1343-1348. doi:10.1007/s00542-009-0822-5
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mashaghi, A, Partovi-Azar, P., Jadidi, T., Nafari, N., Esfarjani, K., Maass, P., et al. (2012). Interfacial water facilitates energy transfer by inducing extended vibrations in membrane lipids. J. Phys. Chem. B 116, 6455-6460. doi:10.1021/jp302478a
CrossRef Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Anvari, M., Panahian, J. S., Nafari, N., et al. (2013a). Enhanced autoionization of water at phospholipid interfaces. J. Phys. Chem. C 117, 510-514. doi:10.1021/jp3119617
CrossRef Full Text
Mashaghi, S., Jadidi, T., Koenderink, G., and Mashaghi, A. (2013b). Lipid nanotechnology. Int. J. Mol. Sci. 14, 4242-4282. doi:10.3390/ijms14024242
CrossRef Full Text
McDowell, M., Leach, A., and Gall, K. (2008). On the elastic modulus of metallic nanowires. Nano Lett. 8, 3613-3618. doi:10.1021/nl801526c
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mitchell, J. S., Zorman, C. A., Kicher, T., Roy, S., and Mehregany, M. (2003). Examination of bulge test for determining residual stress, Young’s modulus, and Poisson’s ratio of 3c-sic thin films. J. Aerosp. Eng. 16, 46-54. doi:10.1061/(ASCE)0893-1321(2003)16:2(46)
CrossRef Full Text
Morone, N., Fujiwara, T., Murase, K., Kasai, R. S., Ike, H., Yuasa, S., et al. (2006). Three-dimensional reconstruction of the membrane skeleton at the plasma membrane interface by electron tomography. J. Cell Biol. 174, 851-862. doi:10.1083/jcb.200606007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Nagle, J. F., and Tristram-Nagle, S. (2000). Structure of lipid bilayers. Biochim. Biophys. Acta 1469, 159-195. doi:10.1016/S0304-4157(00)00016-2
CrossRef Full Text
Neder, J., West, B., Nielaba, P., and Schmid, F. (2010). Coarse-grained simulations of membranes under tension. J. Chem. Phys. 132, 115101. doi:10.1063/1.3352583
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Popescu, G., Ikeda, T., Goda, K., Best-Popescu, C. A., Laposata, M., Manley, S., et al. (2006). Optyczny pomiar napięcia błony komórkowej. Phys. Rev. Lett. 97, 218101. doi:10.1103/PhysRevLett.97.218101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Sansom, D. M. S. P., and Biggin, P. C. (2010). Molecular Simulations and Biomembranes: From Biophysics to Function, 1st Edn. Cambridge, UK: Royal Society of Chemistry.
Schmidt, D., and MacKinnon, R. (2008). Voltage-dependent k+ channel gating and voltage sensor toxin sensitivity depend on the mechanical state of the lipid membrane. Proc. Natl. Acad. Sci. U.S.A. 105, 19276-19281. doi:10.1073/pnas.0810187105
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Seto, H., Yamada, N., Nagao, M., Hishida, M., and Takeda, T. (2008). Bending modulus of lipid bilayers in a liquid-crystalline phase including anomalous swelling regime estimated by neutron spin echo experiments. Eur. Phys. J. E Soft Matter 26, 217-223. doi:10.1140/epje/i2007-10315-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Thakkar, F. M., Maiti, P., Kumarana, V., and Ayappa, K. (2011). Weryfikacja skalowania dla sztywności zginania błon dwuwarstwowych przy użyciu modeli mezoskalowych. Soft Matter 7, 3963-3966. doi:10.1039/c0sm00876a
CrossRef Full Text
Tierney, K. J., Block, D. E., and Longo, M. L. (2005). Elasticity and phase behavior of DPPC membrane modulated by cholesterol, ergosterol and ethanol. Biophys. J. 89, 2481-2493. doi:10.1529/biophysj.104.057943
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
West, B. (2008). Interakcje lipidowo-białkowe w membranach lipidowych. Ph.D. thesis, University of Bielefeld, Bielefeld.
West, B., Brown, F. L. H., and Schmid, F. (2009). Membrane-protein interactions in a generic coarse-grained model for lipid bilayers. Biophys. J. 96, 101. doi:10.1529/biophysj.108.138677
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text