Próbkowanie definiuje się jako, „Proces pomiaru wartości chwilowych sygnału czasu ciągłego w postaci dyskretnej.”
Próbka to fragment danych pobrany z całości danych, które są ciągłe w dziedzinie czasu.
Gdy źródło generuje sygnał analogowy i jeśli ma on być zdigitalizowany, posiadający 1s i 0s tj, Wysoki lub Niski, sygnał musi być dyskretyzowany w czasie. Ta dyskretyzacja sygnału analogowego jest nazywana próbkowaniem.
Następujący rysunek przedstawia sygnał czasu ciągłego x (t) i sygnał próbkowany xs (t). Kiedy x (t) jest mnożony przez okresowy ciąg impulsów, otrzymuje się sygnał próbkowany xs (t).
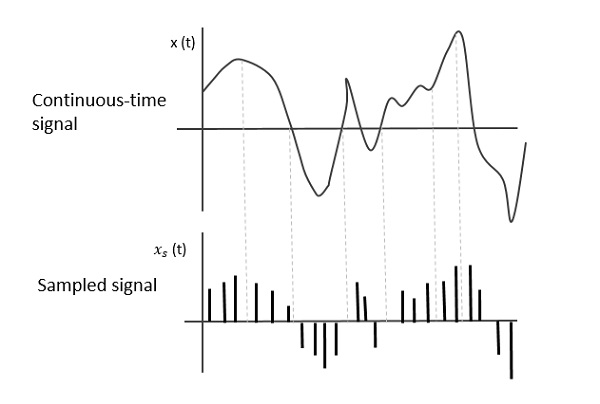
Sampling Rate
Aby zdyskretyzować sygnały, odstęp między próbkami powinien być stały. Ta przerwa może być określona jako okres próbkowania Ts.
$Próbkowanie: Częstotliwość = \frac{1}{T_{s}} = f_s$
Gdzie,
-
$T_{s}$ jest czasem próbkowania
-
$f_{s}$ jest częstotliwością próbkowania lub częstotliwością próbkowania
Częstotliwość próbkowania jest odwrotnością okresu próbkowania. Ta częstotliwość próbkowania, może być po prostu nazywana częstotliwością próbkowania. Częstotliwość próbkowania oznacza liczbę próbek pobieranych na sekundę, lub dla skończonego zestawu wartości.
Aby sygnał analogowy mógł być zrekonstruowany z sygnału cyfrowego, częstotliwość próbkowania powinna być brana pod uwagę. Szybkość próbkowania powinna być taka, aby dane w sygnale wiadomości nie zostały utracone, ani nie nakładały się na siebie. Stąd ustalono częstotliwość, zwaną Nyquist rate.
Nyquist Rate
Załóżmy, że sygnał jest ograniczony pasmem, bez składowych częstotliwości wyższych niż W Hertz. Oznacza to, że W jest najwyższą częstotliwością. Dla takiego sygnału, w celu efektywnego odtworzenia sygnału oryginalnego, częstotliwość próbkowania powinna być dwa razy większa od najwyższej częstotliwości.
Co oznacza,
$f_{S}$ = 2W$
Gdzie,
-
$f_{S}$ jest częstotliwością próbkowania
-
W jest najwyższą częstotliwością
Ta częstotliwość próbkowania jest nazywana częstotliwością Nyquista.
Twierdzenie zwane, Sampling Theorem, zostało sformułowane na podstawie teorii szybkości Nyquista.
Twierdzenie próbkowania
Twierdzenie próbkowania, które jest również nazywane twierdzeniem Nyquista, dostarcza teorii wystarczającej częstotliwości próbkowania w kategoriach szerokości pasma dla klasy funkcji, które są ograniczone pasmem.
Twierdzenie próbkowania stwierdza, że „sygnał może być dokładnie odtworzony, jeśli jest próbkowany z szybkością fs, która jest większa niż dwukrotność maksymalnej częstotliwości W.”
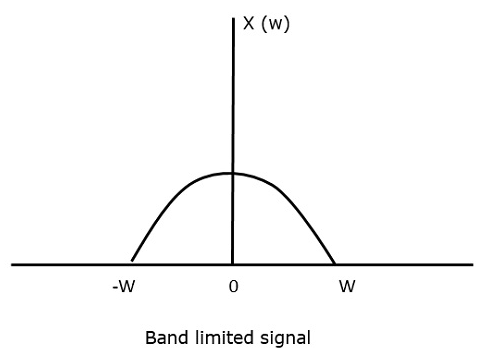
Aby zrozumieć to twierdzenie próbkowania, rozważmy sygnał ograniczony pasmem, tj, sygnał, którego wartość jest niezerowa w przedziale od -W do W herców.
Sygnał taki jest reprezentowany jako $x(f) = 0 dla |fertów > W$
Dla sygnału ciągłego czasu x (t), sygnał ograniczony pasmem w dziedzinie częstotliwości, może być reprezentowany jak pokazano na poniższym rysunku.
Potrzebujemy częstotliwości próbkowania, częstotliwości, przy której nie powinno być utraty informacji, nawet po próbkowaniu. W tym celu mamy współczynnik Nyquista, że częstotliwość próbkowania powinna być dwa razy większa od częstotliwości maksymalnej. Jest to krytyczna szybkość próbkowania.
Jeśli sygnał x(t) jest próbkowany powyżej szybkości Nyquista, oryginalny sygnał może być odzyskany, a jeśli jest próbkowany poniżej szybkości Nyquista, sygnał nie może być odzyskany.
Następujący rysunek wyjaśnia sygnał, jeśli jest próbkowany z szybkością większą niż 2w w dziedzinie częstotliwości.
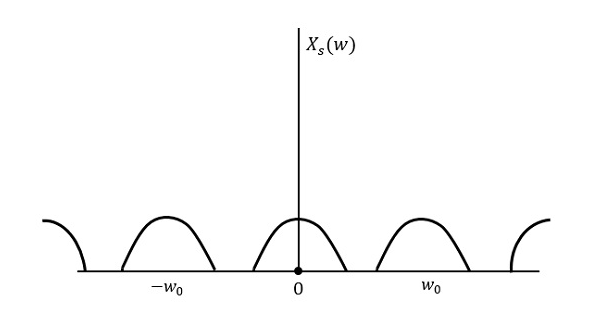
Powyższy rysunek przedstawia transformatę Fouriera sygnału $x_{s}(t)$. Tutaj informacja jest odtwarzana bez żadnych strat. Nie ma mieszania, a zatem odzyskiwanie jest możliwe.
Przekształcenie Fouriera sygnału $x_{s}(t)$ ma postać
$X_{s}(w) = \frac{1}{T_{s}}suma{n = – \infty}^ \infty X(w-nw_0)$
Gdzie $T_{s}$ = okres próbkowania i $w_{0}$ = \frac{2 \i}{T_s}$
Zobaczmy, co się stanie, jeśli częstotliwość próbkowania będzie równa dwukrotności najwyższej częstotliwości (2W)
To oznacza,
$f_{s} = 2W$
Gdzie,
-
$f_{s}$ jest częstotliwością próbkowania
-
W jest najwyższą częstotliwością
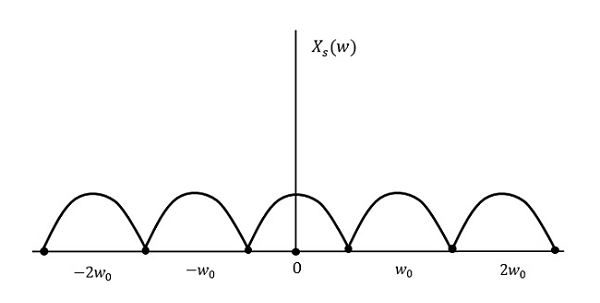
Wynik będzie taki jak na powyższym rysunku. Informacja jest zastępowana bez żadnych strat. Stąd, jest to również dobra częstotliwość próbkowania.
Teraz spójrzmy na warunek,
$f_{s} Wzorzec wynikowy będzie wyglądał jak na poniższym rysunku.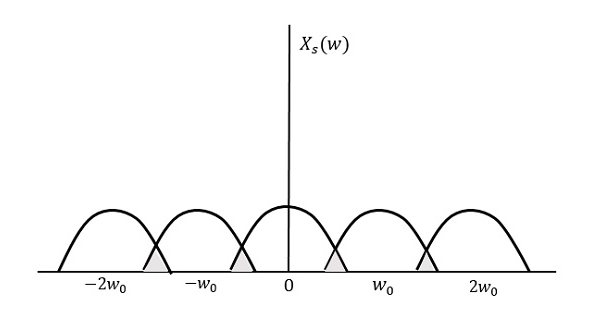
Z powyższego wzorca możemy zaobserwować, że następuje nakładanie się informacji, co prowadzi do mieszania się i utraty informacji. To niepożądane zjawisko nadmiernego nakładania się informacji nazywane jest Aliasingiem.
Aliasing
Aliasing można określić jako „zjawisko polegające na tym, że składowa o wysokiej częstotliwości w widmie sygnału, przyjmuje tożsamość składowej o niskiej częstotliwości w widmie jego próbkowanej wersji.”
Środki zaradcze podejmowane w celu zmniejszenia efektu aliasingu to –
-
W sekcji nadajnika PCM, przed próbkowaniem, stosowany jest dolnoprzepustowy filtr antyaliasingowy w celu wyeliminowania niepożądanych składowych o wysokiej częstotliwości.
-
Sygnał, który jest próbkowany po filtrowaniu, jest próbkowany z szybkością nieco wyższą niż szybkość Nyquista.
Ten wybór szybkości próbkowania wyższej niż szybkość Nyquista, pomaga również w łatwiejszym zaprojektowaniu filtra rekonstrukcyjnego w odbiorniku.
Zakres transformaty Fouriera
Ogólnie obserwuje się, że szukamy pomocy szeregu Fouriera i transformaty Fouriera w analizie sygnałów, a także w udowadnianiu twierdzeń. To dlatego, że –
-
Przekształcenie Fouriera jest rozszerzenie serii Fouriera dla sygnałów nieokresowych.
-
Przekształcenie Fouriera jest potężnym narzędziem matematycznym, które pomaga zobaczyć sygnały w różnych domenach i pomaga analizować sygnały łatwo.
-
Dowolny sygnał może być zdekomponowany w kategoriach sum sinusów i kosinusów przy użyciu tej transformaty Fouriera.
W następnym rozdziale omówmy pojęcie kwantyzacji.