Wyobraź sobie Wszechświat!

Zagraj mi piosenkę o przesunięciu Dopplera! (tekst)
Przepraszamy, Twoja przeglądarka nie obsługuje elementu audio, prosimy o rozważenie aktualizacji.

Czy zauważyłeś, że kiedy mija Cię pojazd ratunkowy z wyciem syreny, ton, który słyszysz, zmienia się w wysokości? Jest to przykład przesunięcia Dopplera i jest to efekt, który jest związany z każdym zjawiskiem falowym (takim jak fale dźwiękowe lub światło).

Rozważmy przypadek, w którym wóz strażacki jest w stanie spoczynku na podjeździe do remizy strażackiej, czekając na strażaków, aby wejść na pokład, jak pokazano na poniższym obrazku. Jeśli syrena jest włączona, słuchacz znajdujący się w pewnej odległości po prawej stronie będzie postrzegał syrenę na tej samej częstotliwości, na której jest emitowana. W rzeczywistości, inna nieruchoma osoba po lewej stronie ciężarówki również usłyszy ten sam ton.

kartoteka fal dźwiękowych emitowanych przez stacjonarny wóz strażacki — Stacjonarny słuchacz po prawej stronie słyszy ten sam ton o częstotliwości 400 Hz emitowany przez wóz strażacki. Okręgi reprezentują fronty fal pochodzące od fal dźwiękowych syreny.
(Credit: NASA’s Imagine the Universe)

Rozważmy teraz, jak ta sytuacja zmienia się, gdy wóz porusza się w kierunku nieruchomego obserwatora ze stałą prędkością, v, jak na zdjęciu poniżej.

kartoteka fal dźwiękowych z nieruchomego wozu strażackiego — Stacjonarny słuchacz po prawej stronie nie słyszy tego samego tonu 400 Hz emitowanego przez wóz strażacki w ruchu. Kółka reprezentują fronty fal dźwiękowych emitowanych przez syrenę.
(Credit: NASA’s Imagine the Universe)

Częstotliwość syreny wozu strażackiego słyszana przez osobę znajdującą się na wozie strażackim nie zmieniła się! Jednak fale w kierunku ruchu wozu wzrastają, ponieważ wóz strażacki dogania swoje własne fale dźwiękowe. Zmiany ciśnienia, które są reprezentowane przez sinusoidy, uderzają w błonę bębenkową nieruchomego obserwatora ze zwiększoną częstotliwością. Dlatego nieruchomy obserwator po prawej stronie odbiera wyższy ton niż ten, który faktycznie emituje wóz strażacki.

Zauważ, że fale za wozem strażackim (po lewej stronie diagramu) są rozłożone, ponieważ syrena oddala się od swojego własnego dźwięku. To spowodowałoby, że nieruchomy obserwator po lewej stronie wozu zauważyłby spadek częstotliwości dźwięku syreny.

Dla źródła poruszającego się w prawo, nieruchomy obserwator po prawej stronie odbierze wyższy ton, a ten po lewej stronie odbierze niższy ton.

Nierelatywistycznie przesunięta dopplerowsko częstotliwość obiektu poruszającego się z prędkością v względem nieruchomego obserwatora, wynosi:

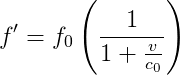
wzór na przesunięcie dopplerowskie fali względem częstotliwości

A długość fali przesuniętej dopplerowsko można pokazać, że wynosi:

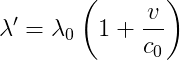
wzór na przesunięcie dopplerowskie fali w zależności od długości fali

W tych dwóch równaniach, c0 to prędkość fali w nieruchomym ośrodku (w tym przypadku prędkość dźwięku), a prędkość to składowa radialna prędkości (część w linii prostej od obserwatora). Oba te wzory są nierelatywistycznymi przybliżeniami, które są prawdziwe tak długo, jak prędkość poruszającego się obiektu jest znacznie mniejsza od prędkości światła.

Jako konwencja, prędkość jest dodatnia, jeśli źródło porusza się od nas i ujemna, jeśli źródło porusza się w kierunku obserwatora.

Tak więc:

jeżeli źródło oddala się (prędkość dodatnia), obserwowana częstotliwość jest niższa, a długość fali większa (przesunięcie ku czerwieni).
jeżeli źródło porusza się w kierunku (prędkość ujemna), obserwowana częstotliwość jest wyższa, a długość fali krótsza (przesunięcie ku błękitowi).

Jak to wpływa na widma odległych obiektów we Wszechświecie? Czy światło doświadcza przesunięcia Dopplera?

Pomyśl o widmie światła widzialnego: czerwony-pomarańczowy-żółty-zielony-niebieski-indigo-fioletowy (w skrócie ROY G. BIV). Jeśli przesunięcie Dopplera działa również dla światła, to musi być możliwe, aby poruszać się tak szybko w kierunku czerwonego światła, że wydaje się ono dla ciebie zielone! Możesz uznać za sprytne użycie tego argumentu, jeśli zostaniesz zatrzymany za przejazd na czerwonym świetle. Okazuje się, że światło z dowolnej części widma elektromagnetycznego może być przesunięte w górę lub w dół pod względem częstotliwości w zależności od twojego względnego ruchu względem emitującego je źródła. Poniższy wykres ilustruje to zjawisko:

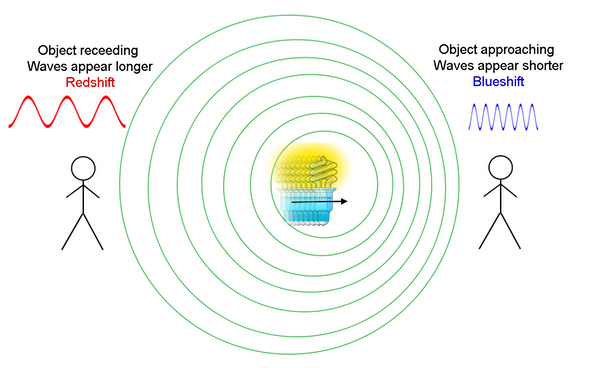
wykres fal z poruszającego się źródła światła — Ilustracja fal świetlnych z poruszającego się źródła światła.
(Credit: NASA’s Imagine the Universe)

Poznasz to jako podobny diagram do tego przedstawiającego wóz strażacki zbliżający się do nieruchomego obserwatora, z tą różnicą, że teraz źródło emituje światło zamiast dźwięku. Zauważ, że region, w którym obserwator postrzega wzrost częstotliwości światła jest określany jako „przesunięcie niebieskie”, a region, w którym obserwator postrzegałby niższą częstotliwość (po lewej stronie na diagramie) jest określany jako „przesunięcie ku czerwieni”. Ważne jest, aby zauważyć, że równania wyprowadzone dla przesunięcia dopplerowskiego dźwięku działają równie dobrze dla poruszających się źródeł światła, pod warunkiem, że źródła światła nie poruszają się z prędkością bliską prędkości światła. Jeśli prędkość względna między źródłem emitującym a obserwatorem byłaby bliska prędkości światła, musielibyśmy wziąć pod uwagę efekty relatywistyczne; a zatem równanie uległoby zmianie.

Więcej informacji Zobacz matematyczne wyprowadzenie równania przesunięcia dopplerowskiego.