In technische toepassingen komen we vaak functies tegen waarvan de waarden abrupt veranderen op een bepaalde waarde van tijd t. Een veel voorkomend voorbeeld is wanneer een spanning in een elektrisch circuit wordt in- of uitgeschakeld op een bepaalde waarde van tijd t.
Later, op deze pagina…
Verplaatste eenheidsstapfunctie
Rechthoekige puls
De waarde van t = 0 wordt meestal genomen als een geschikte tijd om de gegeven spanning in of uit te schakelen.
Het schakelproces kan wiskundig worden beschreven door de functie die de Eenheidsstapfunctie wordt genoemd (ook bekend als de Heaviside-functie naar Oliver Heaviside).
De Eenheidsstapfunctie
Definitie: De eenheidsstapfunctie, `u(t)`, is gedefinieerd als
`u(t)={: {(0, t < 0), (1, t > 0) :}`
Dat wil zeggen, u is een functie van de tijd t, en u heeft waarde nul als de tijd negatief is (voordat we de schakelaar omzetten); en waarde één als de tijd positief is (vanaf het moment dat we de schakelaar omzetten).
Grafiek van `f(t)=u(t)`, de eenheidsstapfunctie.
Waarde op t = 0?
In sommige leerboeken zie je de eenheidsstapfunctie gedefinieerd als waarde 1 op t = 0, als volgt:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
We zouden de discontinuïteit op onze grafiek als volgt aangeven:
Grafiek van `f(t)=u(t)`, de eenheidsstapfunctie, met `f(0) = 1`.
Ook zie je soms de waarde gegeven als `f(0) = 0.5`.
In dit werk maakt het voor onze berekeningen niet veel uit, dus we blijven de eerste interpretatie gebruiken, en tekenen onze grafieken dienovereenkomstig.
Shifted Unit Step Function
In veel schakelingen worden golfvormen toegepast op gespecificeerde intervallen anders dan `t=0`. Zo’n functie kan worden beschreven met behulp van de verschoven (ook wel vertraagde) eenheidsstapfunctie.
Definitie van verschoven eenheidsstapfunctie
Een functie die waarde `0` heeft tot het tijdstip `t = a` en daarna waarde `1` heeft, wordt geschreven:
`u(t-a)={: (0, als, t < a), (1, als, t > a) :}`
Voorbeeld 1 – Verschoven eenheidsstapfunctie
`f(t) = u(t – 3)`
De vergelijking betekent dat f(t) de waarde `0` heeft als `t < 3` en `1` als `t > 3`.
De schets van de golfvorm is als volgt:
Grafiek van `f(t)=u(t-3)`, een verschoven stap-eenheidsfunctie.
Rechthoekige puls
Een veel voorkomende situatie in een schakeling is dat op een bepaald tijdstip (zeg t = a) een spanning wordt aangelegd en later, op t = b (zeg), weer wordt weggenomen. We schrijven zo’n situatie met behulp van stapfuncties per eenheid als:
`V(t) = u(t – a) – u(t – b)`
Deze spanning heeft sterkte `1`, duur `(b – a)`.
Voorbeeld 2 – Rechthoekige puls
De grafiek van `V(t) = u(t – 1,2) – u(t – 3,8)` ziet er als volgt uit. De duur is hier `3,8 – 1,2 = 2,6`.
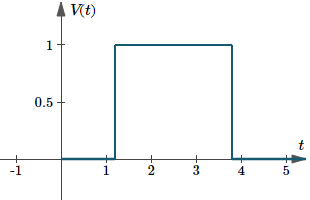
Grafiek van `V(t)=u(t-1.2)-u(t-3.8)`, een voorbeeld van een rechthoekige puls.
Oefeningen
Grafiek papier nodig?
Schrijf de volgende functies in termen van eenheidsstapfunctie(s). Schets elke golfvorm.
(a) Een bron van 12 V wordt ingeschakeld op t = 4 s.
Antwoord
Omdat de spanning op t = 4 wordt ingeschakeld, moeten we u(t – 4) gebruiken. We vermenigvuldigen met 12 omdat dat de spanning is.
We schrijven de functie als volgt:
`V(t)=12-u(t-4)`.
Hier is de grafiek:
Grafiek van `V(t)=12-u(t-4)`, een verschoven stapfunctie.
(b) `V(t)={: (1, 0 < t < a),(0, t > a) :}`
(Neem aan dat a > 0.)
Antwoord
In woorden, de spanning heeft waarde `1` tot het tijdstip `t = a`. Daarna wordt hij uitgeschakeld.
We hebben een “rechthoekige puls”-situatie en moeten deze formule gebruiken:
`V(t) = u(t – a) – u(t – b)`
In ons voorbeeld begint de puls op `t = 0`, dus gebruiken we `u(t)`, en eindigt op `t = a`, dus gebruiken we `u(t – a)`.
Dus de vereiste functie is:
`V(t)=1-` `=u(t)-u(t-a)`
Grafiek van `V(t)=u(t)-u(t-a)`, een verschoven eenheidsstapfunctie.
(c) Eén cyclus van een blokgolf, `f(0) = 4`, amplitude = `4`, periode = `2` seconden.
Antwoord
`f(0) = 4` betekent dat we beginnen bij waarde `4`.
Als de hele golf periode `2` heeft, en het is een blokgolf, dan betekent dit dat voor de helft van de tijd de waarde (positief) `4` is en de andere helft `-4`.
Dus voor de eerste seconde heeft hij waarde `4`, voor de tweede seconde is de functiewaarde `-4`.
We schrijven dit, met behulp van de “rechthoekige puls” formule van hiervoor:
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
De grafiek van deze eerste cyclus is:
Grafiek van `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, een blokgolf.
(d) De eenheid Ramp-functie (d.w.z.`f(t) = t` voor `t > 0`)
Antwoord
De eenheidshellingfunctie heeft helling `1` , begint bij `t = 0` , en gaat door `(0, 0)`.
Dus de spanningsfunctie is gegeven door:
`V(t) = t – u(t)`
De grafiek van de functie is:
Grafiek van `V(t)=t – u(t)`, de unit ramp-functie.
(e) Eén cyclus van een zaagtandgolfvorm (d.w.z. `f(t)=t – u(t)`).d.w.z. `f(t)=a/b t` voor `0 < t < b`. Neem aan dat `a > 0`.)
Antwoord
Onze grafiek begint bij `t = 0` en heeft helling `a / b`. Hij eindigt bij `t = b`.
Dus onze functie zal zijn:
`f(t)=a/b t – {u(t)-u(t-b)}`
De grafiek van onze functie:
Grafiek van `f(t)=a/b t – {u(t)-u(t-b)}`, een zaagtandgolfvorm.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t 5) :}`
Antwoord
In dit voorbeeld is onze functie `V(t) = 2t + 8` die helling `2` en `V`-intercept `8` heeft.
Het signaal is alleen ingeschakeld tussen `t = 3` en `t = 5`. De rest van de tijd staat het uit.
Dus onze spanningsfunctie zal zijn:
`V(t) `= (2t+8) -{u(t – 3)- u(t – 5)}`
De grafiek ziet er als volgt uit:
Grafiek van `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}`. De stippellijn is `V(t) = 2t + 8`.
top
Zoek IntMath
Online calculus solver
Deze calculus solver kan een breed scala aan wiskundeproblemen oplossen.
Ga naar: Online calculus solver