Leerdoelen
Aan het eind van dit deel zul je in staat zijn om:
- Empotentiaalvlakken en equipotentiaallijnen kunnen definiëren
- Het verband tussen equipotentiaallijnen en elektrische veldlijnen kunnen verklaren
- Potentiaallijnen voor één of twee puntladingen in kaart kunnen brengen
- Beschrijf de potentiaal van een geleider
- Vergelijk en contrasteer equipotentiaallijnen en hoogtelijnen op topografische kaarten
We kunnen elektrische potentialen (spanningen) picturaal voorstellen,net zoals we tekeningen hebben gemaakt om elektrische velden te illustreren. Dat is niet verwonderlijk, want de twee begrippen zijn verwant. We zien in figuur een geïsoleerde positieve puntlading en de bijbehorende elektrische veldlijnen, die uitstralen van een positieve lading en eindigen op negatieve ladingen. We gebruiken blauwe pijlen om de grootte en richting van het elektrisch veld weer te geven, en we gebruiken groene lijnen om plaatsen weer te geven waar de elektrische potentiaal constant is. Dit noemt men equipotentiaalvlakken in drie dimensies, of equipotentiaallijnen in twee dimensies. De term equipotentiaal wordt ook gebruikt als zelfstandig naamwoord, dat verwijst naar een equipotentiaallijn of -oppervlak. De potentiaal voor een puntlading is overal gelijk op een denkbeeldige bol met straal r die de lading omgeeft. Dit is waar omdat de potentiaal voor een puntlading gegeven is door V = kq/r en dus dezelfde waarde heeft in elk punt dat op een gegeven afstand van de lading ligt. Een equipotentiaalgebied is een cirkel in het tweedimensionale beeld van figuur 1. Omdat de elektrische veldlijnen radiaal van de lading af wijzen, staan ze loodrecht op de equipotentiaallijnen.
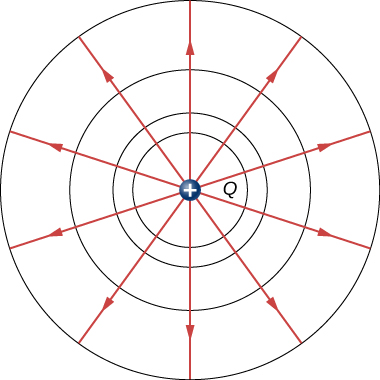
Het is belangrijk op te merken dat equipotentiaallijnen altijd loodrecht staan op elektrische veldlijnen. Er is geen arbeid nodig om een lading langs een equipotentiaal te verplaatsen, omdat Delta V = 0. De arbeid is dus
De arbeid is nul als de richting van de kracht loodrecht op de verplaatsing staat. De kracht is in dezelfde richting als de equipotentiaal, en de verplaatsing langs een equipotentiaal moet loodrecht op de equipotentiaal staan. Preciezer gezegd, de arbeid is gerelateerd aan het elektrisch veld door
&= q\vec{E} \cdot \vec{d} &= qEd, cos , \theta \ &= 0.
Merk op dat in vergelijking \5, \(E) en \(F) de grootheden van respectievelijk het elektrisch veld en de kracht symboliseren. Noch \(q) noch \(E) is nul en \(d) is ook niet nul. Dus moet de waarde 0 zijn, wat betekent dat de waarde 90° moet zijn. Met andere woorden, beweging langs een equipotentiaal staat loodrecht opE.
Een van de regels voor statische elektrische velden en geleiders is dat het elektrisch veld loodrecht op het oppervlak van een geleider moet staan. Dit impliceert dat een geleider in statische situaties een equipotentiaaloppervlak is. Er kan geen spanningsverschil zijn over het oppervlak van een geleider, of er zullen ladingen vloeien. Een van de toepassingen van dit feit is dat een geleider kan worden vastgezet op wat wij beschouwen als nul volt door hem met de aarde te verbinden met een goede geleider – een proces dat aarding wordt genoemd. Aarden kan een nuttig veiligheidsinstrument zijn. Zo zorgt aarding ervoor dat de metalen behuizing van een elektrisch apparaat op nul volt staat ten opzichte van de aarde.
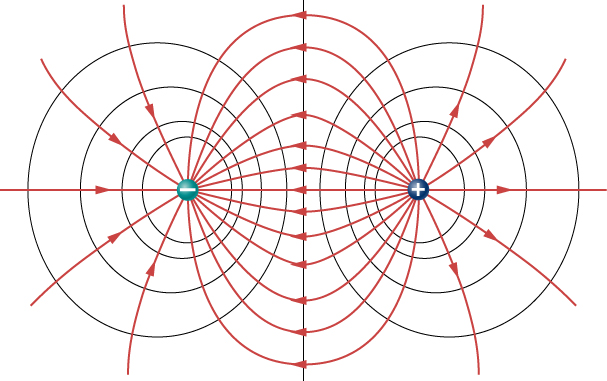
Omdat een geleider een equipotentiaal is, kan hij elk equipotentiaaloppervlak vervangen. Bijvoorbeeld, in figuur
(Pagina-index{2}) kan een bolvormige geleider de puntlading vervangen, en het elektrisch veld en de potentiaalvlakken buiten de bol zullen veranderen, wat de bewering bevestigt dat een bolvormige geladen verdeling gelijkwaardig is aan een puntlading in het centrum.
Figuur
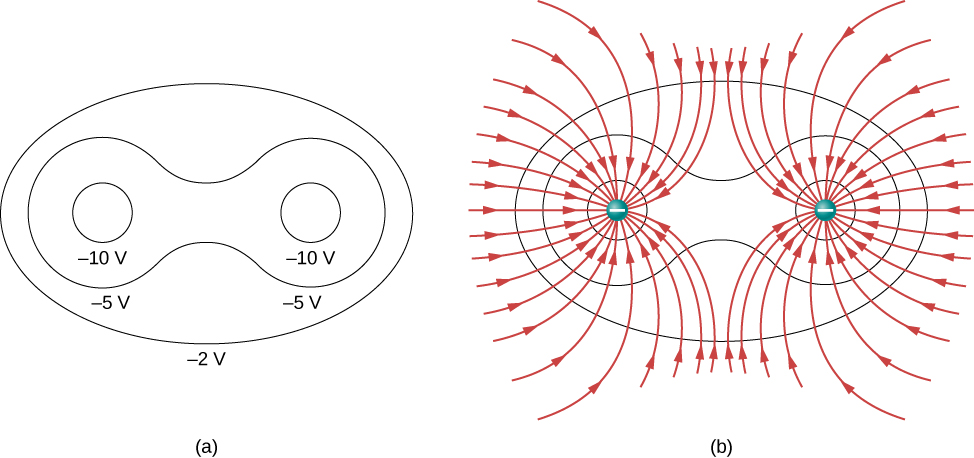
(Pagina-index{2}) toont het elektrisch veld en de equipotentiallijnen voor twee gelijke en tegengestelde ladingen. Gegeven de elektrische veldlijnen kunnen de equipotentiaallijnen eenvoudig getekend worden door ze loodrecht op de elektrische veldlijnen te zetten.Omgekeerd kunnen gegeven de equipotentiaallijnen, zoals in figuur (Pagina-index{2a}), de elektrische veldlijnen getekend worden door ze loodrecht op de equipotentiaallijnen te zetten, zoals in figuur (Pagina-index{2b}).
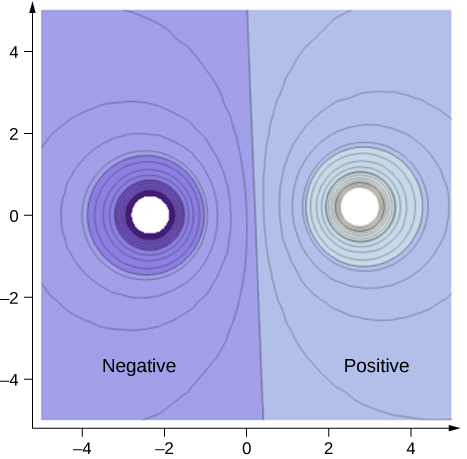
Om je intuïtie te verbeteren, tonen we een driedimensionale variant van de equipotentiaal in een systeem met twee tegengestelde ladingen. De figuur toont een driedimensionale kaart van de elektrische potentiaal, waarbij de lijnen op de kaart equipotentiaalvlakken voorstellen. De heuvel ligt bij de positieve lading, en het dal bij de negatieve lading. Ver weg van de ladingen is de potentiaal nul.Merk op dat de afsnijding bij een bepaalde potentiaal impliceert dat de ladingen zich op geleidende bollen met een eindige straal bevinden.
Figuur(PaginaIndex{4}): Elektrische potentiaalkaart van twee tegengestelde ladingen van gelijke grootte op geleidende bollen. De potentiaal is negatief bij de negatieve lading en positief bij de positieve lading. Deze dynamische afbeelding is gemaakt met CalcPlot3D en kan hier worden bekeken.
Een tweedimensionale kaart van het doorsnedevlak dat beide ladingen bevat, is te zien in figuur (Pagina-index{5}). De lijn die op afstand ligt van de twee tegengestelde ladingen komt overeen met de nulpotentiaal, omdat op de punten op de lijn de positieve potentiaal van de positieve lading de negatieve potentiaal van de negatieve lading opheft. Equipotentiaallijnen in het doorsnedevlak zijn gesloten lussen, die niet noodzakelijk cirkels zijn, omdat op elk punt de netto potentiaal de som is van de potentialen van elke lading.
Note
Bekijk deze simulatie om de equipotentiaalvlakken en elektrische velden voor veel standaard ladingsconfiguraties te observeren en aan te passen. Er valt heel wat te ontdekken.
Een van de belangrijkste gevallen is dat van de bekende parallelle geleidende platen in figuur
6}. Tussen de platen zijn de equipotentialen gelijkmatig verdeeld en evenwijdig. Hetzelfde veld zou kunnen worden gehandhaafd door geleidende platen op de equipotentiaallijnen te plaatsen bij de afgebeelde potentialen.
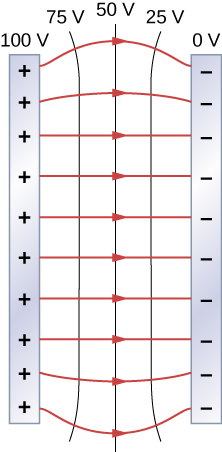
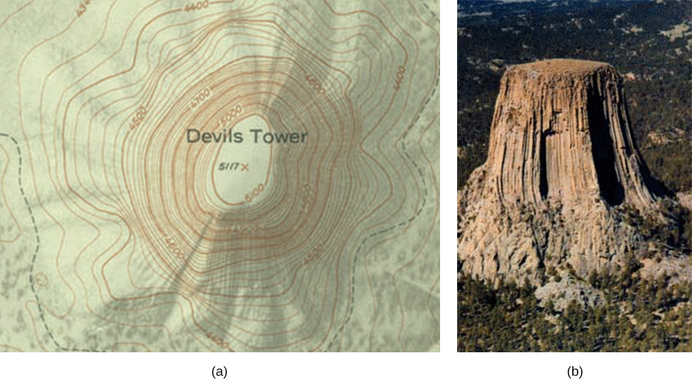
Bekijk de parallelle platen in figuur (Pagina-index{6}). Deze hebben equipotentiaallijnen die evenwijdig zijn aan de platen in de tussenruimte en op gelijke afstand van elkaar liggen. Een voorbeeld hiervan (met voorbeeldwaarden) is gegeven in figuur 26. Voor de zwaartekracht op heuvels kunnen we een soortgelijke reeks equipotentiaal-isolijnen tekenen. Als de helling van een heuvel even groot is, zijn de isolijnen langs die helling evenwijdig aan elkaar. Bovendien zouden in gebieden met een constante helling de isolijnen gelijkmatig verdeeld zijn. Een voorbeeld van echte topografische lijnen is te zien in figuur 7.
Voorbeeld (Pagina-index{1}): Equipotentiaallijnen berekenen
Je hebt de equipotentiaallijnen van een puntlading gezien inFiguur \(\PaginaIndex{1}\). Hoe berekenen we ze? Bijvoorbeeld, als we een puntlading hebben bij de oorsprong, wat zijn dan de equipotentiaalvlakken waarbij de potentiaal (a) 100 V, (b) 50 V, (c) 20 V, en (d) 10 V is?
Strategie
Stel de vergelijking voor de potentiaal van een puntlading gelijk aan een constante en los op voor de overige variabele(n). Bereken vervolgens de nodige waarden.
Oplossing
In V = k\dfrac{q}{r}\), laat V een constante zijn. De enige overblijvende variabele is r; daarom is \(r = k\dfrac{q}{V} =constant). De equipotentiaalvlakken zijn dus bollen om de oorsprong. Hun plaatsen zijn:
- (r = k\dfrac{q}{V} = \links(8.99 keer 10^9 \, Nm^2/C^2rechts)}{(10 keer 10^{-9} C)}{100 \, V} = 0,90 \, m\);
- (r = k\dfrac{q}{V} = \left(8.99 keer 10^9, Nm^2/C^2rechts)\dfrac{(10 keer 10^{-9} C)}{50, V} = 1.8 \, m\);
- (r = k\}{q}{V} = \links(8,99 \tmaal 10^9 \, Nm^2/C^2}rechts)\dfrac{(10 \tmaal 10^{-9} C)}{20 \, V} = 4.5 \, m\);
- (r = k\frac{q}{V} = \links(8,99 \tmaal 10^9 \, Nm^2/C^2}rechts)\dfrac{(10 \tmaal 10^{-9} C)}{10 \, V} = 9,0 \, m\).
Belangrijk
Dit betekent dat equipotentiaaloppervlakken rond een puntlading bollen zijn met een constante straal, zoals eerder is aangetoond, met welbepaalde lokaties.
voorbeeld: Potentiaalverschil tussen tegengesteld geladen parallelle platen
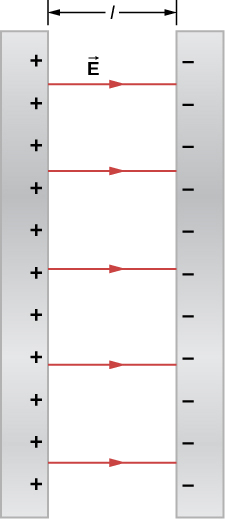
Twee grote geleidende platen hebben gelijke en tegengestelde ladingen, met een oppervlakteladingsdichtheid van 6,81 maal10^{-7} C/m², zoals in figuur
(PaginaIndex{8}) is te zien. De afstand tussen de platen is l = 6,50 mm.
- Wat is het elektrisch veld tussen de platen?
- Wat is het potentiaalverschil tussen de platen?
- Wat is de afstand tussen equipotentiaalvlakken die onderling 100 V verschillen?
Strategie
- Omdat de platen als “groot” worden beschreven en de afstand ertussen niet, benaderen we ze elk als een oneindig vlak, en passen we het resultaat uit de wet van Gauss uit het vorige hoofdstuk toe.
- Gebruik \Delta V_{AB} = – \int_A^B \vec{E} \cdot d\vec{l}).
- Omdat het elektrisch veld constant is, zoek de verhouding van 100 V tot het totale potentiaalverschil; bereken vervolgens dit deel van de afstand.
Oplossing
a. Het elektrisch veld is van de positieve naar de negatieve plaat gericht zoals in de figuur, en de grootte ervan wordt gegeven door
&= dfrac{6.81 imes 10^{-7} C/m^2}{8.85 \times 10^{-12} C^2/N m^2} &= 7.69 \times 10^4 \, V/m.
b. Om het potentiaalverschil tussen de platen te vinden, gebruiken we een pad van de negatieve naar de positieve plaat dat tegen het veld in is gericht. De verplaatsingsvector d(dvec{l}) en het elektrisch veld (\vec{E}) zijn antiparallel zodat (\vec{E}}cdot d\vec{l} = – E, dl}). Het potentiaalverschil tussen de positieve plaat en de negatieve plaat is dan
&= E \int dl \ &= El \ &= (7.69 maal 10^4V/m)(6,50 maal 10^{-3}m) &= 500 \, V \eind{align*}]
c. Het totale potentiaalverschil is 500 V, dus 1/5 van de afstand tussen de platen is de afstand tussen potentiaalverschillen van 100 V. De afstand tussen de platen is 6,5 mm, dus zal er 1,3 mm zijn tussen potentiaalverschillen van 100 V.
Betekenis
Je hebt nu een numerieke berekening gezien van de plaatsen vanequipotentialen tussen twee geladen parallelle platen.
PageIndex{1})
Wat zijn de equipotentiaalvlakken voor een oneindige lijnlading?
Antwoord
oneindige cilinders met constante straal, met de lijnlading als as
Ladingsverdeling op geleiders
In Voorbeeld \PaginaIndex{1})
met een puntlading vonden we dat de equipotentiaalvlakken de vorm hadden van bollen, met de puntlading in het middelpunt. Aangezien een geleidende bol in elektrostatisch evenwicht een bolvormig equipotentiaaloppervlak is, zouden we verwachten dat we een van de oppervlakken in Voorbeeld(PaginaIndex{2}) kunnen vervangen door een geleidende bol en buiten de bol een identieke oplossing kunnen vinden. De oplossing aan de binnenkant zal echter heel anders zijn.
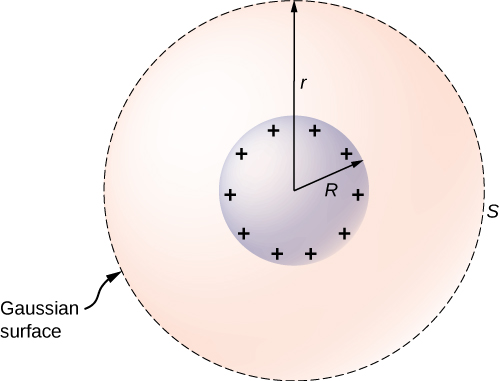
Om dit te onderzoeken, beschouwen we de geïsoleerde geleidende bol vanFiguur \(PaginaIndex{9}\) die een straal R heeft en een overmatige lading q. Om het elektrisch veld zowel binnen als buiten de bol te vinden, moeten we opmerken dat de bol geïsoleerd is, zodat de veranderingsverdeling van het oppervlak en het elektrisch veld van die verdeling sferisch symmetrisch zijn. We kunnen het veld dus voorstellen als E(r)= E(r)= E(r)=dat{r}). Om E(r)te berekenen passen we de wet van Gauss toe op een gesloten boloppervlak S met straal r dat concentrisch is met de geleidende bol.Omdat E(r)constant is en E(r)= E(r)op de bol,
&=E(r) 4:00pi r^2.
Voor \(r < R) is \(S) binnen de geleider, dus herinner je van onze vorige studie van de wet van Gauss dat \(q_{enc} = 0) en de wet van Gauss geeft \(E(r) = 0), zoals verwacht binnen een geleider in evenwicht. Als r > R), dan omsluit S de geleider zodat q_{enc} = q\). Uit de wet van Gauss volgt
Het elektrisch veld van de bol kan dus geschreven worden als
en
Zoals verwacht is in het gebied \(r \geq R\) het elektrisch veld van een lading q op een geïsoleerde geleidende bol met straal R gelijk aan het elektrisch veld van een puntlading q in het middelpunt van de bol.
Om de elektrische potentiaal binnen en buiten de bol te vinden moet voor q(r = 0) de potentiaal gelijk zijn aan die van een geïsoleerde puntlading q gelegen op r = 0,
simpelweg door de overeenkomst van het elektrisch veld.
Voor \(r < R, \, E = 0\) is V(r) in dit gebied dus constant. Omdat V(R) = q/4\pi \epsilon_0 R),
Met dit resultaat laten we zien dat
voor twee geleidende bollen met stralen \(R_1) en \(R_2), met een oppervlakteladingdichtheid van respectievelijk \(R_1) en \(R_2), die met elkaar verbonden zijn door een dunne draad, zoals te zien is in Figuur 10. De bollen zijn voldoende gescheiden zodat elk kan worden behandeld alsof het geïsoleerd was (afgezien van de draad). Merk op dat de verbinding door de draad betekent dat dit hele systeem een equipotentiaal moet zijn.

We hebben zojuist gezien dat de elektrische potentiaal aan het oppervlak van een geïsoleerde, geladen geleidende bol met straal Ris
Nu zijn de bollen verbonden door een geleider en hebben ze dus dezelfde potentiaal; Daarom
en
De netto lading op een geleidende bol en de ladingsdichtheid aan het oppervlak zijn verwant door q = sigma (4 x R^2). Als we deze vergelijking in de vorige invoegen, dan vinden we
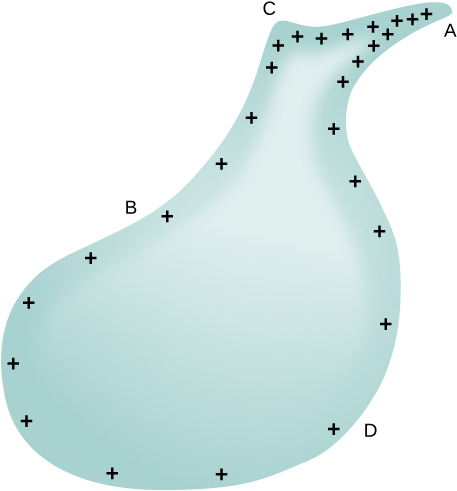
Het is duidelijk dat twee bollen verbonden door een dunne draad geen typische geleider zijn met een variabele kromtestraal. Niettemin geeft dit resultaat tenminste een kwalitatief idee van hoe de ladingsdichtheid varieert over het oppervlak van een geleider. De vergelijking geeft aan dat waar de kromtestraal groot is (punten B en D in figuur 1), E en Sigma klein zijn.
Ook hebben de ladingen de neiging dichter te zijn waar de kromte van het oppervlak groter is, zoals blijkt uit de ladingsverdeling op onevenvormig metaal (figuur 1). De oppervlakteladingsdichtheid is hoger op plaatsen met een kleine kromtestraal dan op plaatsen met een grote kromtestraal.
Een praktische toepassing van dit fenomeen is de bliksemafleider, eenvoudigweg een geaarde metalen staaf met een scherp uiteinde dat naar boven wijst. Wanneer positieve lading zich in de grond ophoopt als gevolg van een negatief geladen wolk boven de grond, wordt het elektrische veld rond het scherpe punt zeer groot. Wanneer het veld een waarde bereikt van ongeveer 3,0 maal 10^6 N/C (de diëlektrische sterkte van de lucht), worden de vrije ionen in de lucht versneld tot zulke hoge energieën dat hun botsingen met luchtmoleculen de moleculen daadwerkelijk ioniseren. De resulterende vrije elektronen in de lucht stromen dan door de staaf naar de aarde, waardoor een deel van de positieve lading wordt geneutraliseerd. Dit voorkomt dat het elektrische veld tussen de wolk en de aarde groot genoeg wordt om een bliksemschicht te veroorzaken in de omgeving van de staaf.
Een belangrijke toepassing van elektrische velden en equipotentiallijnen betreft het hart. Het hart vertrouwt op elektrische signalen om zijn ritme te handhaven. De beweging van elektrische signalen zorgt ervoor dat de kamers van het hart samentrekken en ontspannen. Wanneer iemand een hartaanval heeft, kan de beweging van deze elektrische signalen verstoord zijn. Een kunstmatige pacemaker en een defibrillator kunnen worden gebruikt om het ritme van de elektrische signalen op gang te brengen. De equipotentiallijnen rond het hart, de thoraxstreek en de hartas zijn nuttige manieren om de structuur en de functies van het hart te controleren. Een elektrocardiogram (ECG) meet de kleine elektrische signalen die tijdens de activiteit van het hart worden opgewekt.
PheT
Play around with this simulation to move point charges around on the playing field and then view the electric field, voltages, equipotential lines, and more.
Bijdragers en toeschrijvingen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), en Bill Moebs met vele auteurs die een bijdrage hebben geleverd. Dit werk is gelicenseerd door OpenStax University Physics onder een Creative Commons Naamsvermelding Licentie (by 4.0).