Cramer’s Regel is een andere methode waarmee stelsels lineaire vergelijkingen kunnen worden opgelost met behulp van determinanten.
In termen van notaties, een matrix is een reeks getallen omsloten door vierkante haken, terwijl determinant een reeks getallen is omsloten door twee verticale balken.
Notaties
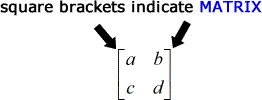
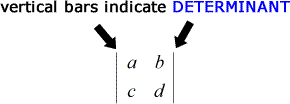
De formule om de determinant van een 2 x 2 matrix te vinden is heel eenvoudig.
Laten we het even op een rijtje zetten:
De determinant van een 2 x 2 matrix
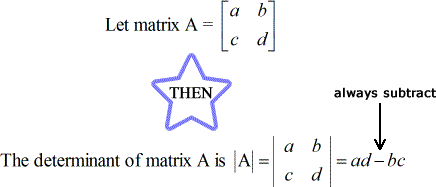
Snelle voorbeelden van hoe de determinanten van een 2 x 2 Matrix te vinden
Voorbeeld 1: Bereken de determinant van de onderstaande matrix A.
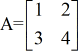
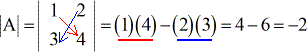
Voorbeeld 2: Bereken de determinant van onderstaande matrix B.
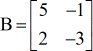
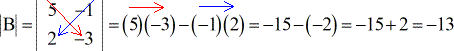
Voorbeeld 3: Bereken de determinant van de onderstaande matrix C.
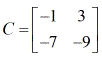
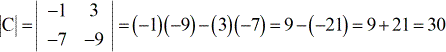
Nadat je weet hoe je de determinant van een matrix van 2 x 2 kunt vinden, ben je nu klaar om de procedures of stappen te leren voor het gebruik van de regel van Cramer. Daar gaan we!
Regels van Cramer voor stelsels lineaire vergelijkingen met twee variabelen
- Geef een lineair stelsel

- Namen toekennen aan elke matrix
coëfficiëntenmatrix:
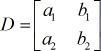
X – matrix:
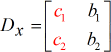
Y – matrix:
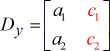
Om voor de variabele x op te lossen.
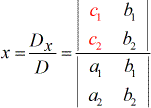
Om op te lossen voor de variabele y.
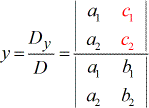
Een paar aandachtspunten bij het bekijken van de formule:
1) De kolommen van \large{x}, \large{y}, en de constante termen \large{c} worden als volgt verkregen:
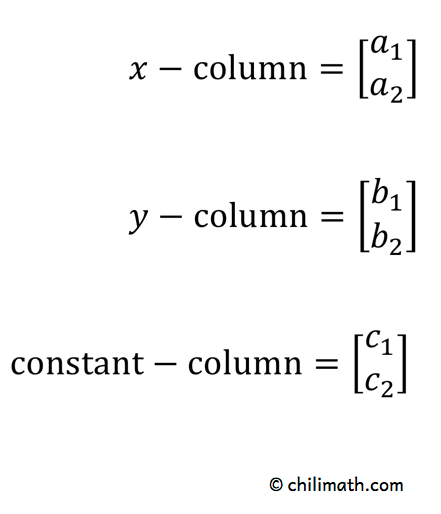
2) De beide noemers in het oplossen van \groot{x} en \groot{y} zijn gelijk. Ze komen uit de kolommen van \groot{x} en \groot{y}.
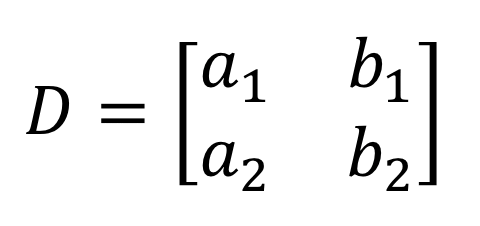
3) Als we naar de teller kijken bij het oplossen van \groot{x}, dan worden de coëfficiënten van de kolom \groot{x} vervangen door de constante-kolom (in rood).
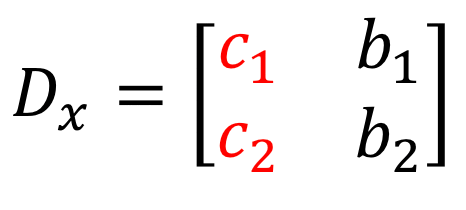
4) Op dezelfde manier, om op te lossen voor \groot{y}, worden de coëfficiënten van \groot{y}-kolom vervangen door de constante-kolom (in het rood).
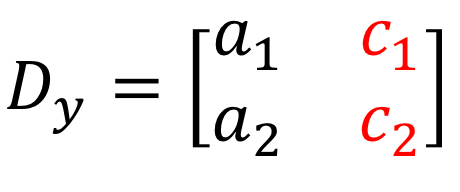
Voorbeelden van hoe je Oplossen van stelsels lineaire vergelijkingen met twee variabelen met behulp van de regel van Cramer
Voorbeeld 1: Los het stelsel met twee variabelen op met de regel van Cramer
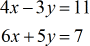
Start met het afleiden van de drie relevante matrices: coëfficiënt, \groot{x}, en \groot{y}. Los vervolgens elke overeenkomstige determinant op.
- Voor de coëfficiëntenmatrix
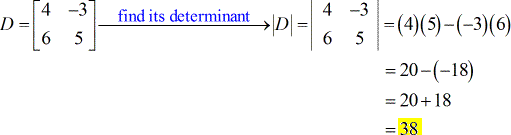
- Voor X – matrix

- Voor Y – matrix

Als alle drie de determinanten zijn berekend, is het tijd om de waarden van \groot{x} en \groot{y} op te lossen met de bovenstaande formule.
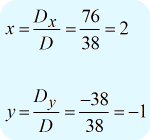
Ik kan het uiteindelijke antwoord schrijven als \links( {x,y} \rechts) = \links( {2, – 1} \rechts)}.
Voorbeeld 2: Los het stelsel met twee variabelen op met de regel van Cramer
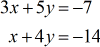
Stel je coëfficiënt-, \groot{x}- en \groot{y}-matrices op uit het gegeven stelsel lineaire vergelijkingen.
Bedenk dat we altijd de producten van de diagonale ingangen aftrekken.
- Voor de coëfficiëntenmatrix (gebruik de coëfficiënten van zowel de x- als de y-variabelen)
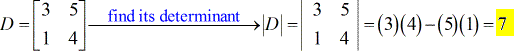
- Voor de X – matrix (vervang de x-kolom door de constante kolom)
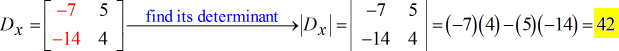
- Voor de Y – matrix (vervang de y-kolom door de constante kolom)
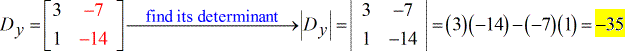
Ik hoop dat je nu een beetje handig bent met het berekenen van de determinant van een 2-dimensionale matrix. Om uiteindelijk de vereiste variabelen op te lossen, krijg ik de volgende resultaten…
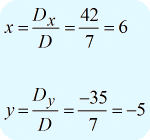
Het uiteindelijke antwoord in puntnotatie schrijvend, kreeg ik {groot} {x,y} \right} = \left( {6, – 5} \right)}.
Voorbeeld 3: Los het stelsel met twee variabelen op met de Regel van Cramer
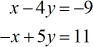
Dit probleem kan eigenlijk vrij eenvoudig worden opgelost met de Eliminatiemethode. Dit komt omdat de coëfficiënten van variabele x “hetzelfde” zijn, maar alleen tegengesteld in tekens ( +1 en -1 ). Om dit op te lossen met de eliminatie methode, voeg je de corresponderende kolommen toe en de x-variabele gaat weg – waardoor je een vergelijking in één stap overhoudt in \groot{y}. Ik vermeld dit omdat elke techniek tekortkomingen heeft en het het beste is om de meest efficiënte te kiezen. Vraag altijd aan je leraar of het goed is om een andere aanpak te gebruiken als de methode voor een bepaald probleem niet gespecificeerd is.
Nu we toch aan het leren zijn hoe we met de regel van Cramer kunnen oplossen, laten we het met deze methode gaan uitwerken.
Ik zal drie matrices construeren ( coëfficiënt, \groot{x} en \groot{y}) en de bijbehorende determinanten berekenen.
- Voor de coëfficiëntenmatrix
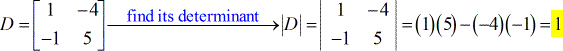
- Voor de X – matrix ( geschreven als hoofdletter D met subscript x )
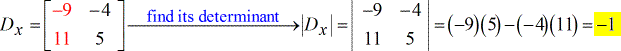
- Voor de Y – matrix (geschreven als hoofdletter D met subscript y)
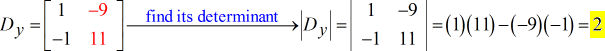
Na het verkrijgen van de waarden van de drie vereiste determinanten, bereken ik \groot{x} en \groot{y} als volgt.
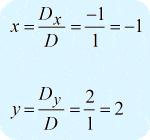
Het uiteindelijke antwoord in de puntvorm is {x,y} \right) = \left( { – 1,2} \right)} .
Voorbeeld 4: Los met de regel van Cramer het stelsel met twee variabelen op
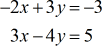
Omdat we al een paar voorbeelden hebben doorgenomen, stel ik voor dat u dit probleem zelf uitprobeert. Vergelijk vervolgens uw antwoorden met de oplossing hieronder.
Als u het de eerste keer goed hebt, bent u een “pro” aan het worden met betrekking tot de Regel van Cramer. Als dat niet zo is, probeer er dan achter te komen wat er fout ging en leer om de volgende keer niet dezelfde fout te maken. Dit is hoe je beter wordt in wiskunde. Bestudeer veel soorten problemen en, nog belangrijker, oefen veel zelfstandig.
- Voor coëfficiëntenmatrix
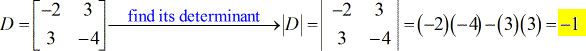
- Voor X – matrix
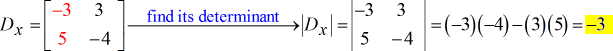
- Voor de Y – matrix
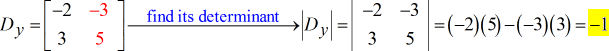
Hieronder zou je het antwoord moeten krijgen…
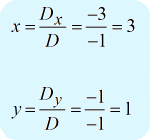
Voorbeeld 5: Los het stelsel met twee variabelen op met de regel van Cramer
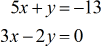
Voor ons laatste voorbeeld heb ik een nul opgenomen in de kolom met de constante. Telkens wanneer je het getal nul in de constante kolom ziet, raad ik je ten zeerste aan de Regel van Cramer te gebruiken om het stelsel van lineaire vergelijkingen op te lossen. Waarom? Omdat de berekening van de determinanten voor de matrices \groot{x} en \groot{y} drastisch super eenvoudig wordt. Kijk zelf maar!
- Voor coëfficiëntenmatrix
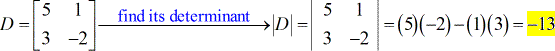
- Voor X – matrix
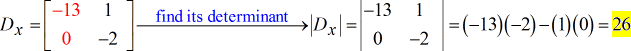
- Voor Y – matrix
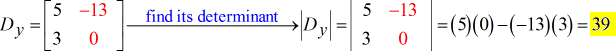
De uiteindelijke oplossing van dit probleem is
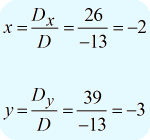
Practicum met werkbladen
Je bent misschien ook geïnteresseerd in:
Cramer’s Regel 3×3