Sampling wordt gedefinieerd als, “Het proces van het meten van de momentane waarden van een continu-tijdsignaal in een discrete vorm.”
Sample is een stukje data dat wordt genomen uit de gehele data die continu is in het tijdsdomein.
Wanneer een bron een analoog signaal genereert en als dat gedigitaliseerd moet worden, met 1en en 0en d.w.z., Hoog of Laag, moet het signaal in de tijd worden gediscontinueerd. Deze discretisatie van een analoog signaal wordt Sampling genoemd.
De volgende figuur toont een continu-tijd signaal x (t) en een bemonsterd signaal xs (t). Wanneer x (t) wordt vermenigvuldigd met een periodieke impulstrein, wordt het bemonsterde signaal xs (t) verkregen.
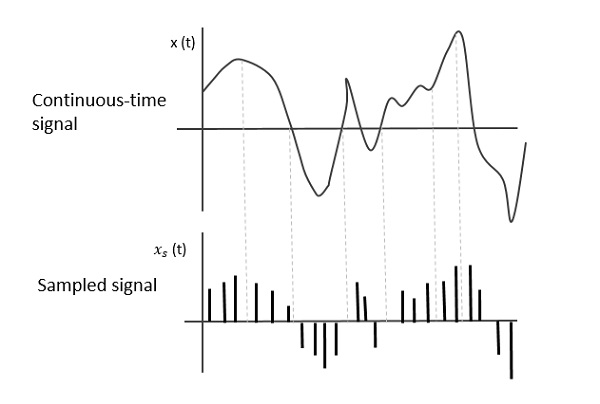
Bemonsteringsfrequentie
Om de signalen te discretiseren, moet de ruimte tussen de monsters worden vastgesteld. Dat verschil kan worden aangeduid als de bemonsteringsperiode Ts.
$Bemonsteringsfrequentie: Frequentie = \frac{1}{T_{s}} = f_s$
Waar,
-
$T_{s}$ is de bemonsteringstijd
-
$f_{s}$ is de bemonsteringsfrequentie of de bemonsteringssnelheid
De bemonsteringsfrequentie is het reciproke van de bemonsteringsperiode. Deze bemonsteringsfrequentie kan eenvoudig worden aangeduid als bemonsteringsfrequentie. De bemonsteringsfrequentie geeft het aantal monsters aan dat per seconde wordt genomen, of voor een eindige reeks waarden.
Om een analoog signaal te kunnen reconstrueren uit het gedigitaliseerde signaal, moet de bemonsteringsfrequentie goed worden overwogen. De bemonsteringsfrequentie moet zodanig zijn dat de gegevens in het berichtsignaal niet verloren gaan of worden overlapt. Daarom is hiervoor een snelheid vastgesteld, die Nyquist-snelheid wordt genoemd.
Nyquist-snelheid
Voorstel dat een signaal bandgelimiteerd is met geen frequentiecomponenten hoger dan W Hertz. Dat betekent dat W de hoogste frequentie is. Voor een dergelijk signaal moet, voor een effectieve reproductie van het oorspronkelijke signaal, de bemonsteringsfrequentie tweemaal de hoogste frequentie bedragen.
Wat betekent,
$f_{S} = 2W$
Waar,
-
$f_{S}$ is de bemonsteringsfrequentie
-
W is de hoogste frequentie
Deze bemonsteringsfrequentie wordt de Nyquist-rate genoemd.
Een stelling, Sampling Theorem genaamd, werd geformuleerd over de theorie van deze Nyquist-snelheid.
Sampling Theorem
De sampling theorem, ook wel Nyquist theorem genoemd, levert de theorie van voldoende sample rate in termen van bandbreedte voor de klasse van functies die bandgelimiteerd zijn.
De bemonsteringstheorem stelt dat “een signaal exact kan worden gereproduceerd als het wordt bemonsterd met de snelheid fs die groter is dan tweemaal de maximumfrequentie W.”
Om deze bemonsteringstheorem te begrijpen, beschouwen we een bandbegrensd signaal, d.w.z, een signaal waarvan de waarde niet nul is tussen een bepaalde -W en W Hertz.
Zulk een signaal wordt voorgesteld als $x(f) = 0 voor |f> > W$
Voor het continue-tijdsignaal x (t) kan het bandgelimiteerde signaal in het frequentiedomein worden voorgesteld zoals in de volgende figuur is aangegeven.
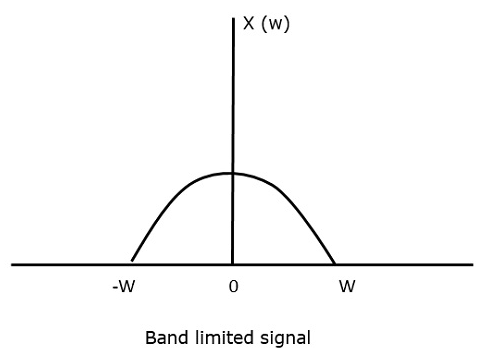
We hebben een bemonsteringsfrequentie nodig, een frequentie waarbij er geen informatieverlies mag optreden, ook niet na bemonstering. Hiervoor hebben we de Nyquist rate dat de bemonsteringsfrequentie twee keer de maximumfrequentie moet zijn. Het is de kritische bemonsteringsfrequentie.
Als het signaal x(t) boven de Nyquist-rate wordt bemonsterd, kan het oorspronkelijke signaal worden teruggevonden, en als het onder de Nyquist-rate wordt bemonsterd, kan het signaal niet worden teruggevonden.
De volgende figuur verklaart een signaal, indien het met een hogere snelheid dan 2w wordt bemonsterd in het frequentiedomein.
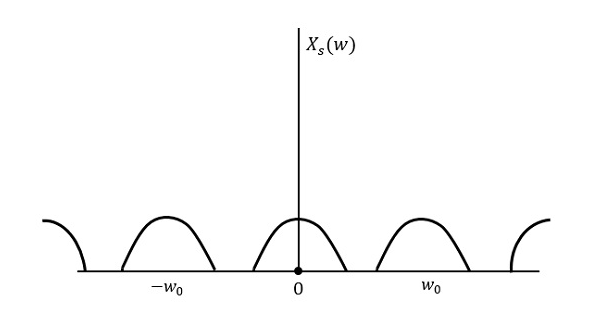
De bovenstaande figuur toont de Fouriertransformatie van een signaal $x_{s}(t)$. Hier wordt de informatie zonder enig verlies gereproduceerd. Er is geen vermenging en dus is herstel mogelijk.
De Fouriertransformatie van het signaal $x_{s}(t)$ is
$X_{s}(w) = \frac{1}{T_{s}}}}som_{n = – \infty}^_infty X(w-nw_0)$
Waarbij $T_{s}$ = Bemonsteringsperiode en $w_{0} = \frac{2 pi}{T_s}$
Laten we eens kijken wat er gebeurt als de bemonsteringsfrequentie gelijk is aan tweemaal de hoogste frequentie (2W)
Dat betekent,
$f_{s} = 2W$
Waar,
-
$f_{s}$ is de bemonsteringsfrequentie
-
W is de hoogste frequentie
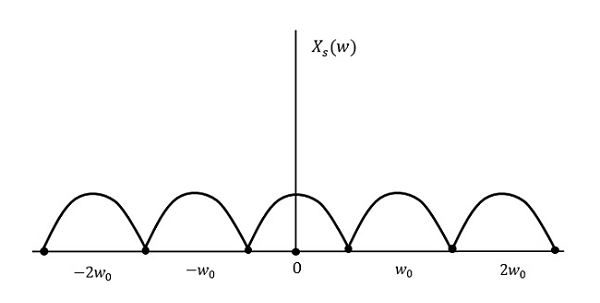
Het resultaat ziet eruit zoals in de bovenstaande figuur. De informatie wordt vervangen zonder enig verlies. Dit is dus ook een goede bemonsteringsfrequentie.
Nu kijken we naar de voorwaarde,
$f_{s} Het resulterende patroon ziet eruit als in de volgende figuur.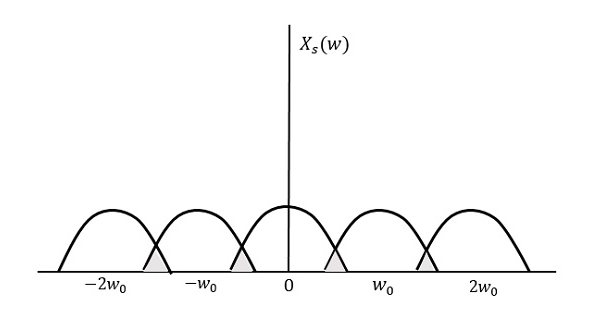
Uit het bovenstaande patroon kunnen we opmaken dat er sprake is van overlapping van informatie, wat leidt tot vermenging en verlies van informatie. Dit ongewenste verschijnsel van overlapping wordt Aliasing genoemd.
Aliasing
Aliasing kan worden aangeduid als “het verschijnsel dat een hoogfrequente component in het spectrum van een signaal, de identiteit aanneemt van een laagfrequente component in het spectrum van de bemonsterde versie ervan.”
De corrigerende maatregelen om het effect van Aliasing te verminderen zijn –
-
In het zendergedeelte van PCM wordt vóór de sampler een laagdoorlatend anti-aliasingfilter gebruikt om de ongewenste hoogfrequente componenten te elimineren.
-
Het signaal dat na de filtering wordt bemonsterd, wordt bemonsterd met een snelheid die iets hoger ligt dan de Nyquist-snelheid.
Deze keuze voor een hogere bemonsteringsfrequentie dan de Nyquist-snelheid maakt het ook gemakkelijker om het reconstructiefilter bij de ontvanger te ontwerpen.
Toepassingsgebied van de Fourier-transformatie
In het algemeen zien we dat we de hulp van Fourier-reeksen en Fourier-transformaties inroepen bij het analyseren van signalen en ook bij het bewijzen van stellingen. Dat komt doordat –
-
De Fouriertransformatie is de uitbreiding van Fourierreeksen voor niet-periodieke signalen.
-
Fouriertransformatie is een krachtig wiskundig hulpmiddel dat helpt om de signalen in verschillende domeinen te bekijken en helpt om de signalen gemakkelijk te analyseren.
-
Elk signaal kan worden ontleed in termen van som van sinussen en cosinussen met behulp van deze Fouriertransformatie.
In het volgende hoofdstuk bespreken we het begrip Kwantisering.