
In deze les maken we u vertrouwd met de basisregels voor het maken van formules en het gebruik van functies. We zijn van mening dat een van de beste manieren om te leren de praktijk is, dus geven we verschillende voorbeelden en leggen we deze in detail uit. We behandelen de volgende onderwerpen:
- rijen en kolommen
- voorbeeld van een wiskundige functie: SUM()
- operators
- operatorvoorrang
- voorbeeld financiële functie: PMT(), betaling lening
- gebruik van een “string”-functie (“string” is steno voor “tekststring”) binnen een formule en het nesten van functies
Formules zijn een mengsel van “functies,” “operatoren,” en “operanden.” Voordat we een paar formules schrijven, moeten we een functie maken, maar voordat we een functie kunnen maken, moeten we eerst de rij- en kolomnotatie begrijpen.
Rijen en kolommen
Om te begrijpen hoe je formules en functies schrijft, moet je weten wat rijen en kolommen zijn.
Rijen lopen horizontaal en kolommen lopen verticaal. Om te onthouden wat wat is, kun je denken aan een kolom die een dak omhoog houdt – kolommen gaan omhoog-omlaag en rijen gaan dus links-rechts.

Kolommen worden aangeduid met letters; rijen met cijfers. De eerste cel in het spreadsheet is A1, wat betekent kolom A, rij 1. De kolommen zijn gelabeld van A-Z. Wanneer het alfabet op is, plaatst Excel er een letter voor: AA, AB, AC… AZ, BA, BC, BC, enz.
Voorbeeld: Functie Som()
Nu gaan we demonstreren hoe je een functie gebruikt.
Je gebruikt functies door ze rechtstreeks in te typen of door de functiewizard te gebruiken. De functiewizard wordt geopend wanneer u ofwel een functie kiest uit het menu “Formules” van de “Functiebibliotheek”. Anders kunt u = in een cel typen en kunt u via een handig keuzemenu een functie kiezen.

De wizard vertelt u welke argumenten u voor elke functie moet opgeven. Er wordt ook een link gegeven naar online instructies als u hulp nodig hebt bij het begrijpen van wat de functie doet en hoe u deze moet gebruiken. Als u bijvoorbeeld =sum in een cel typt, laat de inline-wizard u zien welke argumenten nodig zijn voor de functie SUM.

Wanneer u een functie typt, staat de wizard inline oftewel recht voor uw vingers. Wanneer u een functie selecteert in het menu “Formules”, is de wizard een pop-upvenster. Hier ziet u de pop-upwizard voor de functie SUM().

Voor onze eerste functie gebruiken we SUM(), dat een lijst met getallen optelt.
Voorstel dat we dit spreadsheet hebben met plannen voor het budgetteren van de vakantie van uw gezin:

Om de totale kosten te berekenen zou u =b2+b3+b4+b5 kunnen schrijven, maar het is gemakkelijker om de functie SUM() te gebruiken.
In Excel zoekt u naar het symbool Σ in de linkerbovenhoek van het Excel-scherm om de knop AutoSum te vinden (wiskundigen gebruiken de Griekse letter Σ voor het optellen van een reeks getallen).
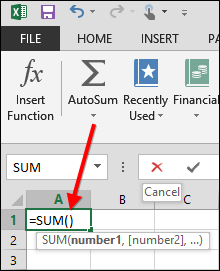
Als de cursor onder de getallen van het gezinsbudget staat, is Excel slim genoeg om te weten dat u de som wilt maken van de lijst met getallen boven waar u de cursor hebt geplaatst, dus markeert het de getallen.

Druk op “enter” om het door Excel geselecteerde bereik te accepteren of gebruik de cursor om te wijzigen welke cellen zijn geselecteerd.
Als u kijkt naar wat Excel in het spreadsheet heeft gezet, ziet u dat het deze functie heeft geschreven:
![]()
In deze formule telt Excel de getallen van B2 tot en met B9 bij elkaar op. Merk op dat we onder rij 5 wat ruimte hebben gelaten, zodat u het vakantiebudget van het gezin kunt aanvullen – de kosten zullen zeker stijgen naarmate de lijst van kinderen met wat ze willen doen en waar ze naartoe willen langer wordt!
Wiskundefuncties werken niet met letters, dus als u letters in de kolom zet, wordt het resultaat weergegeven als “#NAAM?”, zoals hieronder te zien is.

#NAAM? geeft aan dat er een soort fout is opgetreden. Dat kan van alles zijn, zoals:
- slechte celverwijzing
- letters in wiskundige functies gebruiken
- vereiste argumenten weglaten
- functienaam verkeerd spellen
- illegale wiskundige bewerkingen zoals delen door 0
De eenvoudigste manier om de argumenten in een berekening te selecteren, is met de muis. U kunt argumenten toevoegen aan of verwijderen uit de lijst met argumenten van de functie door het vakje dat Excel tekent wanneer u de muis beweegt of in een andere cel klikt, groter of kleiner te maken.
Wij hebben op de bovenkant van het door Excel getekende vakje geklikt om “vliegtickets” uit het budget te halen. U ziet het symbool van het dradenkruis dat u kunt tekenen om het geselecteerde bereik groter of kleiner te maken.

Druk op “enter” om de resultaten te bevestigen.
Berekeningsoperatoren
Er zijn twee soorten operatoren: wiskunde en vergelijking.
Er zijn andere operatoren die niets met wiskunde te maken hebben, zoals “&”, wat betekent dat je twee tekenreeksen aan elkaar moet koppelen (aaneenrijgen). Bijvoorbeeld, =”Excel” & ” is Leuk” is gelijk aan “Excel is Leuk”.
Nu kijken we naar vergelijkingsoperatoren.
Zoals je hierboven kunt zien, werken vergelijkingsoperatoren met getallen en tekst.
Note, als je =”a”>”b” in een cel invoert, staat er “FALSE” omdat “a” niet groter is dan “b”. “b” komt na “a” in het alfabet, dus “a” > “b” of “b” > “a.”
Operator Order Precedence
Orderingsvolgorde is een idee uit de wiskunde. Excel moet dezelfde regels volgen als de wiskunde. Dit onderwerp is gecompliceerder, dus haal even adem en laten we erin duiken.
Order precedence betekent de volgorde waarin de computer het antwoord berekent. Zoals we in Les 1 hebben uitgelegd, is de oppervlakte van een cirkel πr2, wat hetzelfde is als π * r * r. Het is niet (πr)2.
Dus je moet de rangorde begrijpen wanneer je een formule schrijft.
In het algemeen kun je het volgende zeggen:
- Excel evalueert eerst de items tussen haakjes en werkt binnenstebuiten.
- Het gebruikt vervolgens de rangorderegels van de wiskunde.
- Wanneer twee items dezelfde rangorde hebben, werkt Excel van links naar rechts.
De rangorde van wiskundeoperatoren wordt hieronder weergegeven, in aflopende volgorde.
Er zijn andere rangorderegels met betrekking tot tekenreeksen en verwijzingsoperatoren. Voor dit moment zullen we het houden bij wat we zojuist hebben behandeld. Laten we nu eens kijken naar enkele voorbeelden.
Voorbeeld: Berekenen van de oppervlakte van een cirkel
De oppervlakte van een cirkel is =PI() * straal ^ 2.
Kijkend naar de tabel hierboven zien we dat exponenten voor vermenigvuldiging komt. De computer berekent dus eerst straal ^ 2 en vermenigvuldigt dat resultaat met Pi.
Voorbeeld: Berekening van een loonsverhoging
Laten we zeggen dat je baas besluit dat je het geweldig doet en dat hij of zij je een loonsverhoging van 10% gaat geven! Hoe zou je je nieuwe salaris berekenen?
Vooreerst, onthoud dat vermenigvuldiging voor optelling komt.
Is het =salaris + salaris * 10% of is het =salaris + (salaris * 10%)?
Voorstel dat je salaris $100 is. Met een loonsverhoging van 10% wordt uw nieuwe salaris:
= 100 + 100 * 10% = 100 + 10 = 110
U kunt het ook zo schrijven:
=100 + (100 * 10%) = 100 + 10 = 110
In het tweede geval hebben we de rangorde expliciet gemaakt door haakjes te gebruiken. Onthoud dat haakjes vóór elke andere bewerking worden geëvalueerd.
De eenvoudigere manier om dit te schrijven is trouwens = salaris * 110%
Een paar voorbeelden meer
Hier is nog een voorbeeld: = 4 * 3 / 2. Wat is het antwoord?
We zien aan de regels in de tabel hierboven dat * en / gelijke voorrang hebben. Dus Excel werkt van links naar rechts, 4 * 3 = 12 eerst, dan deelt dat door 2 om 6 te krijgen.
Ook hier zou je dat expliciet kunnen maken door te schrijven = (4 * 3) / 2
En hoe zit het met = 4 + 3 * 2?
De computer ziet zowel * als + operatoren. Dus volgens de voorrangsregels (vermenigvuldigen gaat voor optellen) berekent hij eerst 3 * 2 = 6 en telt er dan 4 bij op om 10 te krijgen.
Als je de voorrangsregels zou willen veranderen zou je schrijven = (4 + 3) * 2 = 14.
Wat dacht je van deze = -1 ^ 3?
Dan is het antwoord -3 omdat de computer berekende = (-1) ^ 3 = -1 * -1 * -1 = -1.
Zo dat zijn een paar voorbeelden van wiskundige volgorde en voorrang, we hopen dat dat helpt om een paar dingen duidelijk te maken over hoe Excel berekeningen uitvoert (en dat is waarschijnlijk genoeg wiskunde om een leven lang mee te gaan voor sommigen van u).
Voorbeeld: Functie Leningbetaling (PMT)
Laten we eens kijken naar een voorbeeld om een leningbetaling te berekenen.
Begin met het maken van een nieuw werkblad.
Opmaak de getallen met dollartekens en gebruik nul decimalen, omdat we nu niet geïnteresseerd zijn in centen, omdat die er niet veel toe doen als je het over dollars hebt (in het volgende hoofdstuk gaan we in detail in op hoe je getallen opmaakt). Bijvoorbeeld, om het rentepercentage op te maken, klik met de rechtermuisknop op de cel en klik op “cellen opmaken”. Kies percentage en gebruik 2 cijfers achter de komma.
Op dezelfde manier maak je de andere cellen op voor “valuta” in plaats van percentage en kies je “getal” voor de looptijd van de lening.

Nu hebben we:

Voeg de functie SUM() toe om de maandelijkse uitgaven te “totaliseren”.

Merk op dat de hypotheekcel niet in het totaal is opgenomen. Excel weet niet dat u dat getal wilt opnemen, omdat daar geen waarde staat. Zorg er dus voor dat u de SUM()-functie naar boven uitbreidt, hetzij door de cursor te gebruiken, hetzij door E2 in te typen waar E3 staat om de hypotheek in de som op te nemen.
Plaats de cursor in de betalingscel (B4).

In het menu Formules selecteert u de vervolgkeuzelijst “Financieel” en vervolgens selecteert u de PMT-functie. De wizard verschijnt:
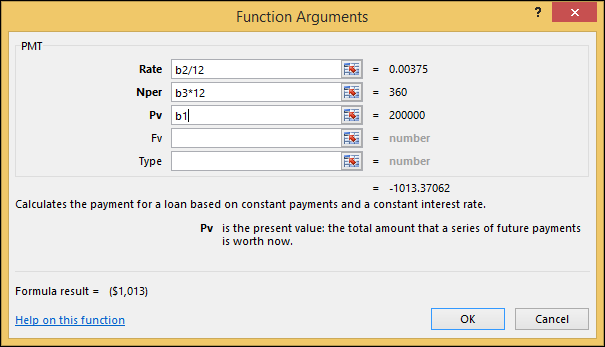
Gebruik de cursor om de “rate.”, “nper” (leentermijn), “Pv” (“contante waarde” of leenbedrag) te selecteren. Merk op dat u het rentepercentage door 12 moet delen, aangezien de rente maandelijks wordt berekend. U moet ook de looptijd in jaren vermenigvuldigen met 12 om de looptijd in maanden te krijgen. Druk op “OK” om het resultaat in de spreadsheet op te slaan.
Merk op dat de betaling als een negatief getal wordt weergegeven: -1013,37062. Om het positief te maken en bij de maandelijkse uitgaven op te tellen, wijs je de hypotheekcel aan (E2). Typ “=-” en gebruik vervolgens de cursor om het betalingsveld aan te wijzen. De resulterende formule is =-B4.

Nu ziet de spreadsheet er als volgt uit:

Uw maandelijkse uitgaven zijn $1.863 – Oei!
Voorbeeld: Tekstfunctie
Hier laten we zien hoe je functies binnen een formule en tekstfuncties kunt gebruiken.
Voorstel dat je een lijst met studenten hebt zoals hieronder afgebeeld. De voor- en achternaam staan in één veld, gescheiden door een komma. We moeten de achternaam en de vaste naam in aparte cellen zetten. Hoe doen we dat?

Om dit probleem aan te pakken, moet je een algoritme gebruiken – dat wil zeggen, een stapsgewijze procedure om dit te doen.
Kijk bijvoorbeeld eens naar “Washington, George.” De procedure om dat in twee woorden te splitsen zou zijn:
- Bereken de lengte van de string.
- Vind de positie van de komma (dit geeft aan waar het ene woord eindigt en het andere begint).
- Kopieer de linkerkant van de tekenreeks tot aan de komma.
- Kopieer de rechterkant van de tekenreeks vanaf de komma tot aan het einde.
Laten we stap voor stap in Excel bespreken hoe je dit doet met “George Washington”.
- Bereken de lengte van de tekenreeks met de functie =LEN(A3) – het resultaat is 18.
- Nu de positie van de komma vinden met deze functie =FIND(“,”,A3″) – het resultaat is 11.
- Neem nu de linkerkant van de tekenreeks tot aan de komma en maak deze geneste formule met het resultaat van stap 1: =LEFT(A3,FIND(“,”,A3)-1). Merk op dat we 1 moeten aftrekken van de lengte omdat FIND de positie van de komma geeft.
Hier ziet dat er allemaal uit wanneer alle functies samen in een formule worden geplaatst. In cel B3 zie je dat deze formule alle informatie uit cel A3 neemt en er “Washington” in invoert.

Dus we hebben “Washington”, nu moeten we nog “George” zien te krijgen. Hoe doen we dat?
Merk op dat we het resultaat van stap 1 in een cel op zichzelf hadden kunnen opslaan, bijvoorbeeld B6, en dan een eenvoudigere formule schrijven =LEFT(A3,B6-1). Maar dat gebruikt één cel voor de intermitterende stap.
- Herinner de positie van de komma of bereken hem opnieuw.
- Bereken de lengte van de tekenreeks.
- Tel de tekens vanaf het einde van de tekenreeks tot de komma.
Neem het aantal tekens uit stap 3 en trek er één van af om de komma en de spatie weg te laten.
Laten we dit stap-voor-stap doen.
Jouw spreadsheet zou er nu ongeveer zo uit moeten zien als in onderstaande schermafbeelding. We hebben de formules als tekst onderaan de spreadsheet gekopieerd, zodat het makkelijker te lezen en te zien is.
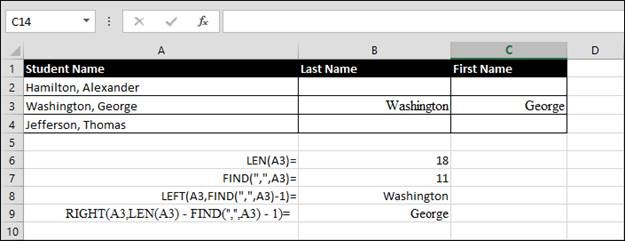
Dat was een beetje moeilijk, maar je hoeft deze formules maar één keer te schrijven.
Komt nog …
Dit is het einde van onze les voor vandaag. U zou nu een vrij goed begrip moeten hebben van formules en functies, rijen en kolommen, en de manier waarop dit alles kan worden gebruikt aan de hand van een aantal concrete voorbeelden.