Introduction
Elastische eigenschappen spelen een belangrijke rol in een aantal membraanprocessen, zoals bijvoorbeeld membraanfusie (Chernomordik and Kozlov, 2008) en modulaties van membraankanaal activiteiten (Schmidt and MacKinnon, 2008; Sansom en Biggin, 2010; Mashaghi et al., 2013b). In cellen worden de buitenste membranen ondersteund door de onderliggende actinenetwerken. De mechanische spanning wordt dan gedomineerd door het bijbehorende actine-cytoskelet op lengteschalen groter dan de maaswijdte van het actinenetwerk (30-300 nm) (Morone et al., 2006). Op kleine lengteschalen, echter, zal de bijdrage van de lipide bilaag domineren. Daarom zijn pogingen ondernomen om de mechanische eigenschappen te bestuderen van bilaagpatches met afmetingen die dicht bij de maaswijdte van het actine-cytoskelet liggen (Claesson et al., 2011).
Wanneer een membraan als een tweedimensionaal lichaam wordt beschouwd, d.w.z. wanneer de dikte wordt verwaarloosd, kunnen de mechanische eigenschappen bij afwezigheid van anisotrofen worden gekarakteriseerd door twee elasticiteitsconstanten volgens de continuüm-elasticiteitstheorie. In de gangbare praktijk van materiaalkarakterisering zijn deze parameters gewoonlijk de elasticiteitsmodulus en de Poisson-verhouding. Schattingen voor de elasticiteitsmodulus van membranen zijn verkregen door experimenten (Tierney et al., 2005; Popescu et al., 2006). Het meten van de Poisson’s ratio is echter niet eenvoudig door de geringe dikte van membranen in het nanometergebied (Mitchell et al., 2003; Martins et al., 2009). Vanuit theoretisch oogpunt worden de mechanische eigenschappen van lipidemembranen meestal onderzocht op basis van de Helfrich Hamiltoniaan. De belangrijkste fysische grootheid die uit dergelijke studies wordt verkregen is de buigstijfheid. De Young’s modulus en Poisson’s ratio zijn onderling gerelateerd door formules die de buigstijfheid omvatten, maar noch Young’s modulus noch Poisson’s ratio zijn tot nu toe afzonderlijk bepaald.
Simulaties en theoretische modellen zijn gebruikt om belangrijke informatie te verstrekken over elastische (Goetz en Lipowsky, 1998; Lindahl en Edholm, 2001; Ayton et al., 2002) en viskeuze eigenschappen van lipide bilayers (Jeon en Voth, 2005). Het onderzoek naar de mechanische eigenschappen van dunne films is niet beperkt tot biomembranen en vertegenwoordigt een actief onderzoeksgebied in de materiaalkunde. Er zijn inspanningen geleverd om de Poisson’s ratio van films gemaakt van verschillende materialen te voorspellen door middel van computersimulaties. Galvao et al. hebben bijvoorbeeld gebruik gemaakt van moleculaire dynamica simulaties met gebruikmaking van reactieve empirische bindingsordenpotentialen om de mechanische eigenschappen van grafeen nanoribbons te onderzoeken (Martins and Galvao, 2010). Baughman et al. hebben een model voorgesteld om de Poisson’s ratio van vezelnetwerken te schatten en hebben dit met succes toegepast op koolstof nanobuis vellen (buckypaper) (Hall et al., 2008).
In dit werk introduceren we een methode om de Poisson’s ratio ν te bepalen in simulaties en passen deze toe op het grofkorrelige lipidemembraan model, dat is geïntroduceerd door Lenz en Schmid (2005). Deze methode is algemeen en toepasbaar op alle andere oppervlakken. Na bepaling van de buigstijfheid kc uit het vermogensspectrum van de hoogtefluctuaties van het membraan, kunnen we de elasticiteitsmodulus E berekenen.
Materialen en Methoden
Monte Carlo simulaties van lipide bilayers met periodieke randvoorwaarden in laterale richtingen werden uitgevoerd voor het grofkorrelige model geïntroduceerd door Lenz en Schmid (2005). In dit model worden amfifielen met één staart beschouwd, die worden voorgesteld door zes staartkorrels en één iets grotere hoofdkraal (met een grootteverhouding van 1-1,1). De kralen die tot één molecuul behoren zijn verbonden via eindig rekbare niet-lineaire elastische (FENE) veren (Grest en Kremer, 1986) met een bindingsrekpotentiaal Figuur 1:
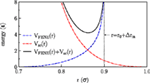
Figuur 1.
Hierbij is r de afstand tussen aangrenzende parels, νFENE karakteriseert de sterkte van de veer, r0 is de optimale bindingslengte (geen uitrekking), en Δrm is de maximale uitrekafstand. De stijfheid van de staarten wordt in rekening gebracht door een harmonische bindingshoekpotentiaal
waarbij θijk de bindingshoek is die bij drie aangrenzende korrels hoort. Zowel de niet-gebonden korrels die tot hetzelfde molecuul behoren als de korrels die tot verschillende moleculen behoren, interageren via een zachte-kernpotentiaal:
waar θ(.) de Heaviside-stappenfunctie is. De oplosmiddelmoleculen worden voorgesteld door een fantoommodel van korrels die met de lipidebolletjes interageren via VSC(r) (met dezelfde parameters als de hoofdparels) maar niet met zichzelf. Alle modelparameters zijn gekozen volgens het gerefereerde model (Lenz en Schmid, 2005) en zijn samengevat in tabel 1.

Tabel 1. Interactiepotentialen van het gerefereerde model en bijbehorende parameters.
Lipide bilayers vertonen een rijk spectrum aan structuren en faseovergangen (Nagle en Tristram-Nagle, 2000; Illya et al., 2005; Seto et al., 2008; Thakkar et al., 2011). De vloeistoftoestand bij hoge temperaturen wordt gekenmerkt door een ongeordende rangschikking van de lipidenstaarten en een relatief hoge lipidenmobiliteit. Bij afkoeling ondergaat deze vloeistoftoestand een faseovergang naar een geltoestand, waarin de lipidemoleculen meer geordend zijn en een lagere mobiliteit hebben. Andere mogelijke fasen zijn de interdigitated fase, waarin lipidestaarten van tegengestelde monolagen interpenetreren.
Door het fasediagram van het gerefereerde model (Lenz, 2007) af te tasten, hebben we eerst lipide bilayers voor ongeveer twee miljoen Monte Carlo (MC) stappen geëquilibreerd om verschillende fasen te produceren voor het doel van dit werk, zie figuur 2. In de gereduceerde eenheden, ϵ/kB voor de temperatuur T en ϵ/σLJ3 voor de druk P, zijn de overeenkomstige thermodynamische variabelen: P = 2 en T = 1,08 voor de gelfase, P = 1 en T = 1,3 voor de vloeistoffase, P = 0,5 en T = 1,16 voor de interdigitatiefase. De karakteristieke parameters voor verschillende fasen met inbegrip van de gemiddelde ketenlengte l¯, dikte van de bilaag d, oppervlakte per lipide A, en keten orde parameter Sz zijn samengevat in tabel 2.

Figuur 2. Snapshots van het gesimuleerde lipidemembraan in de (A) gel, (B) vloeistof, en (C) interdigitated fase. Lipide’s hoofd kralen en staart kraal worden weergegeven in rood en groen, respectievelijk.
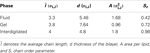
Tabel 2. Karakteristieke parameters van lipide bilayers.
Simulaties werden uitgevoerd onder constante temperatuur en druk conditie (NPT ensemble) voor lipide bilayers met verschillende afmetingen. Om het vermogensspectrum van de oppervlakhoogtefluctuaties te onderzoeken, simuleerden we een bilaag waarvan de bovenste en onderste bladen bestaan uit 64 × 64 lipidemoleculen. Voor het oplosmiddelenmodel werden ongeveer 17000-72000 bolletjes gekozen (het precieze aantal hangt af van de gesimuleerde fase). Voor het uitvoeren van de analyse van de Poisson’s ratio, hebben we rechthoekige bilayers bestaande uit 12 × 24 lipidemoleculen per leaflet geëquilibreerd tot drie verschillende fasen.
Om zowel E als ν te bepalen, moeten we een van deze elastische constanten afzonderlijk bepalen. Gebruikmakend van de periodieke randvoorwaarden introduceren we een methode om de Poisson’s ratio voor het oppervlak te berekenen (Abedpour et al., 2010). De Poisson’s ratio is de negatieve verhouding van de transversale deformatieveranderingen gedeeld door de axiale deformatieveranderingen in een lichaam wanneer het wordt uitgerekt of samengedrukt langs de axiale richting onder de spanning onder de proportionele limiet. Voor de infinitesimale diagonale spanningen kan de Poisson-verhouding worden vervangen door de verhouding van de relatieve lengteveranderingen als νij = -ΔLi/ηjLi, waarbij ηj ≡ ΔLj/Lj is gedefinieerd als de fractie van de axiale lengteverandering. Hier i ≠ j en i = x, y, en z. In de methode, die we hier presenteren de lengte tussen naburige lipiden wordt herschaald met een factor (1 + η) in axiale richting, laten we zeggen y-richting, en de daaropvolgende verandering van de simulatie box grootte in loodrechte richtingen, in dit geval x-en z-richting, worden gecontroleerd. Terwijl de herschaalde dooslengte (1 + η) Ly constant wordt gehouden, voor het fixeren van de druk in de simulaties, worden de doosafmetingen nu alleen in de x- en z-richting toegestaan te fluctueren. Wanneer de aanvankelijke gemiddelde lengtes in x- en z-richting Lx en Lz waren, worden na het herschalen nieuwe gemiddelde waarden van Lx + ΔLx en Lz + ΔLz bereikt door het systeem gedurende een paar MC-stappen opnieuw in evenwicht te brengen, zie figuur 3.
 www.frontiersin.org
www.frontiersin.orgFiguur 3. Snapshots van de lipidemembraan in vloeibare fase als (A) initiële configuratie, (B) na het verhogen van de bilaag grootte in y-richting met een factor van (1 + η), en (C) de ontspannen bilaag vaststelling van de membraan grootte in y-richting en variabele x-richting. Als gevolg van de positieve Poisson’s ratio voor de bilaag in deze fase wordt de membraangrootte in x-richting gereduceerd en na een aantal MC-stappen geëquilibreerd.
Tijdens de simulatie, om de thermalisatie procedure te versnellen na het uitbreiden van de doos langs de axiale richting, hebben we de temperatuur in het systeem iets verhoogd, wat resulteert in het produceren van de meer mobiliteit voor de deeltjes. Voor de vloeistoffase hebben we de begintemperatuur ingesteld op T = 1,3 en deze vervolgens veranderd in T = 1,4 voor ongeveer 400 extra stappen en daarna teruggeschakeld naar de oorspronkelijke waarde. Evenzo waren voor de gel- en interdigitatiefasen de begintemperaturen T = 1,08 en T = 1,16 en werd overgeschakeld op T = 1,2 en T = 1,3, respectievelijk.
Een gangbare analyse van de elastische eigenschappen van een membraan berust op de Helfrich Hamiltoniaan (Helfrich, 1973), die de kosten beschrijft van de elastische vrije enthalpie die samenhangt met fluctuaties van de membraanhoogte (afwijkingen van het platte oppervlak). Wanneer het membraan wordt geparametriseerd in cartesische coördinaten (x,y) →(x,y,h(x,y)) (Monge gauge), wordt de Helfrich Hamiltoniaan, voor kleine fluctuaties, gegeven door
waarbij kc de buigstijfheid is en σ de oppervlaktespanning. Vergelijking (4) wordt toegepast wanneer het membraan wordt beschouwd als een lichaam met een dikte van nul. Een veralgemeende elastische theorie voor membranen met eindige dikte werd voorgesteld door Brannigan en Brown (2006) en recentelijk toegepast op het Lenz-Schmid model (West et al., 2009; Neder et al,
Om h(x, y) uit de simulaties te bepalen, hebben we het (x, y)-vlak in een regelmatig rooster met tussenruimten 2σLJ verdeeld, in elke cel (i, j) de gemiddelde z-coördinaten z+(i, j) en z-(i, j) van de hoofdkorrels in de bovenste en onderste folder bepaald, respectievelijk, en de hoogte h(i, j) – /2 berekend (het gemiddelde h¯ werd er vervolgens van afgetrokken). Voor een membraan van zijdelingse grootte L × L voorspelt Eq. (4) voorspeld:
voor het vermogensspectrum van de fluctuaties, waarbij ĥ(q) de Fouriertransformatie is van h(x, y) bij golfvector q, q = |q|, en <> staat voor een evenwichtsgemiddelde. In de numerieke berekening wordt ĥ(q) berekend uit een discrete Fouriertransformatie van h(i, j). Het is duidelijk dat Eq. (5) alleen kan gelden voor een q-bereik 2π/L ≪ q ≪ 2π/σLJ, waarin noch de eindige systeemgrootte noch de (atomistische) korrelgrootte de fluctuaties beïnvloedt. Het bijbehorende q-bereik voor systeemgroottes die binnen redelijke rekentijd haalbaar zijn is helaas niet groot, maar fits van < |ĥ(q)|2 > ∕kBTL2 als functie van q2 in een bereik van 0.5 ≤ q2 ≤ 1 leveren een goede overeenkomst op met Eq. (5) voor onze maten.
Resultaten en Discussies
In Tabel 3 worden de verkregen Poisson-verhoudingen νyx, νzx, en νxy evenals νzy voor verschillende fasen samengevat. Zoals aangetoond in figuur 4, is de op deze wijze verkregen Poisson’s ratio onafhankelijk van de herschalingsfactor η zolang η niet te groot is, hetgeen leidt tot vernietiging van de membraanstructuur, noch te klein, hetgeen niet voldoende vrije ruimte oplevert voor deeltjes om te bewegen. Volgens tabel 3 en figuur 4 hebben de vloeibare en de geïnterdigiteerde fasen dezelfde gemeten Poisson-verhouding voor zowel x- als y-richting. Dit betekent dat deze twee fasen isotroop zijn in het vlak van de bilaag. Dit is echter niet meer het geval voor de gel-fase. De metingen tonen aan dat een bilaag in de gel-fase zich gedraagt als een anisotroop materiaal, dat twee duidelijk verschillende waarden heeft voor de twee verschillende richtingen in het vlak van de bilaag.

Tabel 3. Elastische constanten verkregen uit simulaties van lipidemembranen in verschillende fasen.

Figuur 4. Ontspanning van -ΔLi/ηjLi in (A) vloeibare, (B) interdigitated, en (C) gel fase. De plateauwaarde die na ongeveer 5000 MC-stappen wordt bereikt, onafhankelijk van de waarde van η, geeft de Poisson-verhouding ν. In de gel-fase, Poisson’s ratio heeft verschillende waarden voor νxy en νyx en deze fase fungeert als een anisotroop oppervlak.
Omgekeerd, wanneer de bilaag werd uitgebreid in de loodrechte richting van het kantelvlak, lipiden reorganiseren zich op zodanige wijze dat de bilaag lateraal kromp. Voor het huidige werk zijn de bindingslengtes van de lipiden in de z-richting (loodrecht op het bilaagvlak) niet herschaald. De reden hiervoor is dat, om het Poisson’s effect waar te nemen, de lengte tussen de bolletjes moet worden herschaald met een factor, die voldoende ruimte oplevert voor de deeltjes om zich te herschikken. In de z-richting moet deze toename zich echter voordoen tussen de gebonden korrels binnen een lipide, hetgeen een verbreking van de binding veroorzaakt. De gerapporteerde waarden voor νzx en νzy zijn de resulterende relatieve lengteveranderingen in de gemiddelde lengte van de bilaag ten gevolge van de laterale uitbreiding van de bilagen in x- en y-richting, respectievelijk.
De verkregen waarden voor de buigstijfheid kc zijn 5,2ϵ voor de vloeibare fase, en 7,6ϵ voor de geïnterdigiteerde fase. Voor de gel- en vloeistoffase komen de resultaten overeen met eerdere rekenkundige rapporten (West, 2008; West et al., 2009) en experimentele bevindingen (Falcioni et al., 1997; Liu en Zhang, 2009). De spectrale dichtheid voor de geïnterdigiteerde fase werd volgens dezelfde methode berekend. Wij rapporteren hier de buigstijfheid voor de geïnterdigiteerde fase. Figuur 5 illustreert de fluctuatiespectra van de hoogte voor de drie bestudeerde fasen en past in Eq. (5).
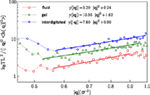
Figuur 5. Fluctuatiespectra voor de vloeistof-, gel-, en interdigitated fasen en fits met Eq. (5).
In de tweedimensionale elasticiteitstheorie is de buigstijfheid kc gerelateerd aan de Poisson’s ratio ν en de Young’s modulus E volgens (Landau et al., 1986)
waarbij d de gemiddelde membraandikte is, waarvoor we, 5,48σLJ, en 4,86σLJ verkrijgen voor respectievelijk de vloeibare, en de geïnterdigiteerde fasen. Door de gevonden waarden voor de Poisson’s ratio’s en de buigstijfheden voor bilayers in twee isotrope fasen in Eq. (6) in te vullen, verkrijgt men de bijbehorende Young’s moduli. De op deze wijze berekende Young’s moduli zijn 0.28 en 0.67 in eenheden van ϵ/σ3 voor respectievelijk de vloeistoftoestand en de interdigitatietoestand. Het is duidelijk dat de waargenomen anisotropiciteit in de gel-fase het niet mogelijk maakt de bovenstaande stelling te gebruiken voor de bilaag in deze fase.
De in dit artikel gepresenteerde benadering zou kunnen worden toegepast op membranen met complexere lipidensamenstellingen, aangezien de experimenteel geverifieerde interactiemodellen voor die lipiden bestaan. De benadering zou ook kunnen worden gecombineerd met meer nauwkeurige simulatie van bilayers. Volledige atomistische simulaties en in het bijzonder ab initio simulaties, zouden in principe nauwkeurigere beschrijvingen van het systeem kunnen opleveren, maar gaan gepaard met een enorme rekenlast (Mashaghi et al., 2012, 2013a).
Conclusie
We hebben Monte Carlo simulaties uitgevoerd van het grofkorrelige lipidenbilaagmodel om inzicht te krijgen in de mechanische eigenschappen van planaire lipidemembranen. Door gebruik te maken van een herschalingsmethode konden we de Poisson’s ratio ν bepalen voor verschillende fasen, naast de buigstijfheid bepaald uit een analyse van de hoogtefluctuaties van het membraan op basis van de Helfrich Hamiltoniaan. Dit stelt ons in staat ook de Young’s modulus E voor verschillende fasen te berekenen. De aanpak is nauwkeurig, gemakkelijk te implementeren en kan worden toegepast op andere membranen zoals grafeen (Abedpour et al., 2010), om de temperatuurafhankelijkheid van de Poisson’s ratio en Young’s modulus te voorspellen. Andere interessante systemen om te bestuderen zijn kristallijne metalen nanodraden waar elasticiteitsmodulus controleert hun structurele prestaties en functionele gedrag, zoals hun resonantiefrequentie onder oscillerende belasting meestal toegepast tijdens de activering en sensing (Chen et al., 2006; McDowell et al., 2008).
Conflict of Interest Statement
De auteurs verklaren dat het onderzoek is uitgevoerd in afwezigheid van commerciële of financiële relaties die kunnen worden opgevat als een potentieel belangenconflict.
Acknowledgments
Wij willen Philipp Maass bedanken voor zijn nuttige discussies.
Abedpour, N, Asgari, R., en Tabar, M. R. R. (2010). Onomkeerbaarheid in reactie op krachten die op grafeenvellen werken. Phys. Rev. Lett. 104, 196804. doi:10.1103/PhysRevLett.104.196804
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Ayton, G., Smondyrev, A., Bardenhagen, S., McMurtry, P., and Voth, G. (2002). Berekening van de bulkmodulus voor een lipide bilaag met niet-kwilibrium moleculaire dynamica simulatie. Biophys. J. 82, 1226-1238. doi:10.1016/S0006-3495(02)75479-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Brannigan, G., and Brown, F. L. H. (2006). Een consistent model voor thermische fluctuaties en eiwit-geïnduceerde vervormingen in lipide bilayers. Biophys. J. 90, 1501. doi:10.1529/biophysj.105.075838
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chen, C., Shi, Y., Zhang, Y., Zhu, J., and Yan, Y. (2006). Grootteafhankelijkheid van de elasticiteitsmodulus in ZnO-nanodraden. Phys. Rev. Lett. 96, 075505. doi:10.1103/PhysRevLett.96.075505
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chernomordik, L. V., and Kozlov, M. M. (2008). Mechanica van membraanfusie. Nat. Struct. Mol. Biol. 15, 675-683. doi:10.1038/nsmb.1455
CrossRef Full Text
Claesson, M., Frost, R., Svedhem, S., and Andersson, M. (2011). Porie-overspannende lipide bilayers op mesoporeus silica met variërende poriegrootte. Langmuir 27, 8974-8982. doi:10.1021/la201411b
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Falcioni, M., Bowick, M. J., Guitter, E., and Thorleifsson, G. (1997). De Poisson-verhouding van kristallijne oppervlakken. Europhys. Lett. 38, 67-72. doi:10.1016/j.jhazmat.2010.12.101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Goetz, R., and Lipowsky, R. (1998). Computersimulaties van bilaagmembranen: zelfassemblage en interfaciale spanning. J. Chem. Phys. 108, 7397-7409. doi:10.1063/1.476160
CrossRef Full Text
Grest, G. S., and Kremer, K. (1986). Moleculaire dynamica simulatie voor polymeren in de aanwezigheid van een warmtebad. Phys. Rev. A 33, 3628-3631. doi:10.1103/PhysRevA.33.3628
CrossRef Full Text
Hall, L., Coluci, V., Galvao, D., Kozlov, M., Zhang, M., Dantas, S., et al. (2008). Tekenverandering van Poisson’s ratio voor koolstof nanobuis vellen. Science 320, 504-507. doi:10.1126/science.1149815
Pubmed Abstract | Pubmed Full Text |Ref Full Text
Helfrich, W. (1973). Elastische eigenschappen van lipide bilayers-theorie en mogelijke experimenten. Z. Naturforsch. C 28, 693.
Illya, G., Lipowsky, R., and Shillcock, J. C. (2005). Effect van ketenlengte en asymmetrie op materiaaleigenschappen van bilaagmembranen. J. Chem. Phys. 122, 1-6. doi:10.1063/1.1917794
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Jeon, J., and Voth, G. (2005). De dynamische stressresponsen op oppervlakteverandering in planaire lipide bilaagmembranen. Biophys. J. 88, 1104-1119. doi:10.1529/biophysj.104.052183
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Landau, L. D., Pitaevskii, L. P., Lifshitz, E. M., and Kosevich, A. M. (1986). Theorie van de Elasticiteit, Deel 7, 3e Edn. Oxford: Butterworth-Heinemann.
Lenz, O. (2007). Computersimulatie van Lipide Bilayers. Ph.D. thesis, Universiteit van Bielefeld, Bielefeld.
Lenz, O., and Schmid, F. (2005). Een eenvoudig computermodel voor vloeibare lipide bilayers. J. Mol. Liq. 117, 147-152. doi:10.1016/j.molliq.2004.08.008
CrossRef Full Text
Lindahl, E., and Edholm, O. (2001). Moleculaire dynamica simulatie van NMR relaxatiesnelheden en langzame dynamica in lipide bilayers. J. Chem. Phys. 115, 4938-4950. doi:10.1529/biophysj.107.121806
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Liu, P., and Zhang, Y. W. (2009). Temperatuursafhankelijke buigstijfheid van grafeen. Appl. Phys. Lett. 94, 231912. doi:10.1063/1.3155197
CrossRef Full Text
Martins, B., and Galvao, D. (2010). Curved graphene nanoribbons: structure and dynamics of carbon nanobelts. Nanotechnology 21, 075710. doi:10.1088/0957-4484/21/7/075710
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Martins, P., Malhaire, C., Brida, S., and Barbier, D. (2009). Over de bepaling van de Poisson’s ratio van gespannen monolaag en bilaag submicron dikke films. Microsyst. Technol. 15, 1343-1348. doi:10.1007/s00542-009-0822-5
Pubmed Abstract | Pubmed Full Text |Ref Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Nafari, N., Esfarjani, K., Maass, P., et al. (2012). Interfaciaal water vergemakkelijkt energieoverdracht door verlengde trillingen in membraanlipiden te induceren. J. Phys. Chem. B 116, 6455-6460. doi:10.1021/jp302478a
CrossRef Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Anvari, M., Panahian, J. S., Nafari, N., et al. (2013a). Verbeterde autoionisatie van water aan fosfolipide interfaces. J. Phys. Chem. C 117, 510-514. doi:10.1021/jp3119617
CrossRef Full Text
Mashaghi, S., Jadidi, T., Koenderink, G., and Mashaghi, A. (2013b). Lipide nanotechnologie. Int. J. Mol. Sci. 14, 4242-4282. doi:10.3390/ijms14024242
CrossRef Full Text
McDowell, M., Leach, A., and Gall, K. (2008). Over de elastische modulus van metalen nanodraden. Nano Lett. 8, 3613-3618. doi:10.1021/nl801526c
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mitchell, J. S., Zorman, C. A., Kicher, T., Roy, S., and Mehregany, M. (2003). Examination of bulge test for determining residual stress, Young’s modulus, and Poisson’s ratio of 3c-sic thin films. J. Aerosp. Eng. 16, 46-54. doi:10.1061/(ASCE)0893-1321(2003)16:2(46)
CrossRef Full Text
Morone, N., Fujiwara, T., Murase, K., Kasai, R. S., Ike, H., Yuasa, S., et al. (2006). Drie-dimensionale reconstructie van het membraanskelet aan de plasmamembraan interface door elektronentomografie. J. Cell Biol. 174, 851-862. doi:10.1083/jcb.200606007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Nagle, J. F., and Tristram-Nagle, S. (2000). Structuur van lipide bilayers. Biochim. Biophys. Acta 1469, 159-195. doi:10.1016/S0304-4157(00)00016-2
CrossRef Full Text
Neder, J., West, B., Nielaba, P., and Schmid, F. (2010). Grofkorrelige simulaties van membranen onder spanning. J. Chem. Phys. 132, 115101. doi:10.1063/1.3352583
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Popescu, G., Ikeda, T., Goda, K., Best-Popescu, C. A., Laposata, M., Manley, S., et al. (2006). Optische meting van de spanning van het celmembraan. Phys. Rev. Lett. 97, 218101. doi:10.1103/PhysRevLett.97.218101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Sansom, D. M. S. P., and Biggin, P. C. (2010). Moleculaire Simulaties en Biomembranen: From Biophysics to Function, 1st Edn. Cambridge, UK: Royal Society of Chemistry.
Schmidt, D., and MacKinnon, R. (2008). Voltage-dependent k+ channel gating and voltage sensor toxin sensitivity depend on the mechanical state of the lipid membrane. Proc. Natl. Acad. Sci. U.S.A. 105, 19276-19281. doi:10.1073/pnas.0810187105
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Seto, H., Yamada, N., Nagao, M., Hishida, M., and Takeda, T. (2008). Bending modulus of lipid bilayers in a liquid-crystalline phase including anomalous swelling regime estimated by neutron spin echo experiments. Eur. Phys. J. E Soft Matter 26, 217-223. doi:10.1140/epje/i2007-10315-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Thakkar, F. M., Maiti, P., Kumarana, V., and Ayappa, K. (2011). Verificatie van schalen voor buigstijfheid van bilaagmembranen met behulp van mesoschaalmodellen. Soft Matter 7, 3963-3966. doi:10.1039/c0sm00876a
CrossRef Full Text
Tierney, K. J., Block, D. E., and Longo, M. L. (2005). Elasticiteit en fasegedrag van DPPC membraan gemoduleerd door cholesterol, ergosterol en ethanol. Biophys. J. 89, 2481-2493. doi:10.1529/biophysj.104.057943
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
West, B. (2008). Lipid-Protein Interactions in Lipid Membranes. Ph.D. thesis, Universiteit van Bielefeld, Bielefeld.
West, B., Brown, F. L. H., and Schmid, F. (2009). Membraan-eiwit interacties in een generiek grofkorrelig model voor lipide bilayers. Biophys. J. 96, 101. doi:10.1529/biophysj.108.138677
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text