Nu we hebben gedefinieerd dat de logaritmische functie y = log b x de inverse functie is van de exponentiële functie y = b x. We kunnen nu overgaan tot het grafisch weergeven van logaritmische functies door te kijken naar de relatie tussen exponentiële en logaritmische functies.
Maar voordat we overgaan tot het grafisch tekenen van logaritmische functies, is het belangrijk dat we ons vertrouwd maken met de volgende termen:
- Het domein van een functie
Het domein van een functie is een verzameling waarden die je in de functie kunt substitueren om een aanvaardbaar antwoord te krijgen.
- Het bereik van een functie
Dit is de verzameling waarden die je verkrijgt na substitutie van de waarden in het domein voor de variabele.
- Asymptoten
Er zijn drie soorten asymptoten, namelijk; verticaal, horizontaal, en schuin. De verticale asymptoot is de waarde van x waarbij de functie grenzeloos dichtbij groeit.
Horizontale asymptoten zijn constante waarden die f(x) benadert als x grenzeloos groeit. Schuine asymptoten zijn eerstegraads polynomen waar f(x) in de buurt komt als x grenzeloos groeit.
Hoe graficeer je logaritmische functies?
Het graficeren van een logaritmische functie kan worden gedaan door de grafiek van de exponentiële functie te bekijken en dan x en y om te wisselen.
De grafiek van een exponentiële functie f (x) = b x of y = b x bevat de volgende kenmerken:
- Het domein van een exponentiële functie is reële getallen (-oneindig, oneindig).
- Het bereik is ook positieve reële getallen (0, oneindig)
- De grafiek van een exponentiële functie gaat normaliter door het punt (0, 1). Dit betekent dat het y – intercept in het punt (0, 1) ligt.
- De grafiek van een exponentiële functie f(x) = b x heeft een horizontale asymptoot bij y = 0.
- Een exponentiële grafiek neemt van links naar rechts af als 0 < b < 1, en dit geval heet exponentieel verval.
- Als de basis van de functie f(x) = b x groter is dan 1, dan neemt de grafiek van links naar rechts toe en heet het exponentiële groei.
Door bovenstaande kenmerken een voor een te bekijken, kunnen we op dezelfde manier kenmerken van logaritmische functies als volgt afleiden:
- Een logaritmische functie zal het domein als (0, oneindig) hebben.
- Het bereik van een logaritmische functie is (-oneindig, oneindig).
- De grafiek van de logaritmische functie gaat door het punt (1, 0), dat voor een exponentiële functie het omgekeerde is van (0, 1).
- De grafiek van een logaritmische functie heeft een verticale asymptoot bij x = 0.
- De grafiek van een logaritmische functie zal van links naar rechts afnemen als 0 < b < 1.
- En als de basis van de functie groter is dan 1, b > 1, dan zal de grafiek van links naar rechts toenemen.
Hoe maak je een grafiek van een logaritmische basisfunctie?
Een logaritmische basisfunctie is in het algemeen een functie zonder horizontale of verticale verschuiving.
Hier volgen de stappen voor het maken van een grafiek van een logaritmische basisfunctie.
- Omdat alle logaritmische functies door het punt (1, 0) gaan, zoeken we het punt op en plaatsen we er een punt bij.
- Om te voorkomen dat de kromme de y-as raakt, tekenen we een asymptoot bij x = 0.
- Als de basis van de functie groter is dan 1, vergroot je de kromme van links naar rechts.
Nu bekijken we de volgende voorbeelden:
Voorbeeld 1
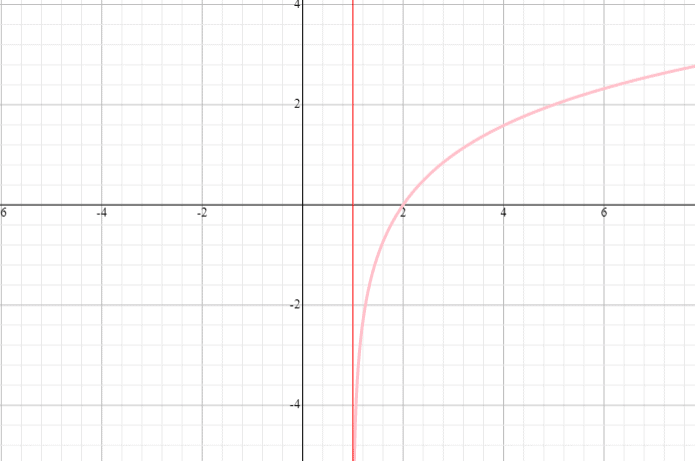
Grafeer de logaritmische functie f(x) = log 2 x en geef het bereik en domein van de functie aan.
Oplossing
- Het spreekt voor zich dat een logaritmische functie het domein en bereik moet hebben van (0, oneindig) en (-oneindig, oneindig)
- Omdat de functie f(x) = log 2 x groter is dan 1, zullen we onze kromme van links naar rechts laten oplopen, zoals hieronder te zien is.
- We kunnen de verticale asymptoot bij x = 0 niet zien, want die wordt verborgen door de y-as.
Voorbeeld 2
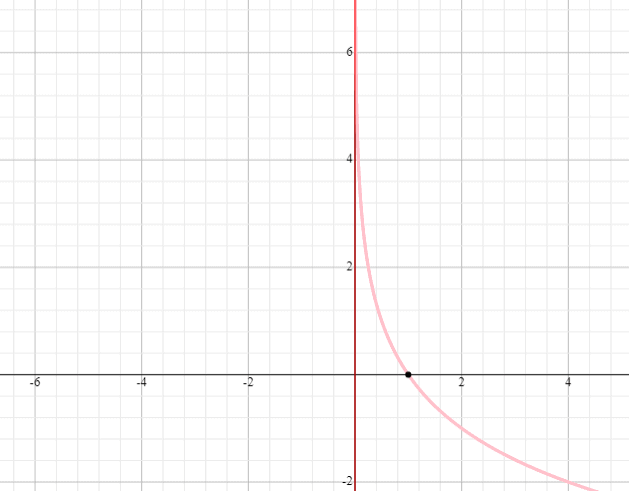
Teken een grafiek van y = log 0,5 x
Oplossing
- Plaats een punt op het punt (1, 0). Alle logaritmische krommen gaan door dit punt.
- Teken een asymptoot bij x = 0.
- Omdat de basis van de functie y = log 5 x kleiner is dan 1, zullen we onze kromme van links naar rechts laten afnemen.
- De functie y = log 5 x zal ook (0, oneindig) en (-infinity, oneindig) als domein en bereik hebben.
Grafiek van een logaritmische functie met horizontale verschuiving
Logaritmische functies met horizontale verschuiving zijn van de vorm f(x) = log b (x + h) of f (x) = log b (x – h), waarbij h = de horizontale verschuiving. Het teken van de horizontale verschuiving bepaalt de richting van de verschuiving. Als het teken positief is, wordt de verschuiving negatief, en als het teken negatief is, wordt de verschuiving positief.
Door toepassing van de horizontale verschuiving worden de kenmerken van een logaritmische functie op de volgende manieren beïnvloed:
- Het x – intercept verschuift een vaste afstand gelijk aan h naar links of naar rechts.
- De verticale asymptoot verschuift een gelijke afstand van h.
- Het domein van de functie verandert ook.
Voorbeeld 3
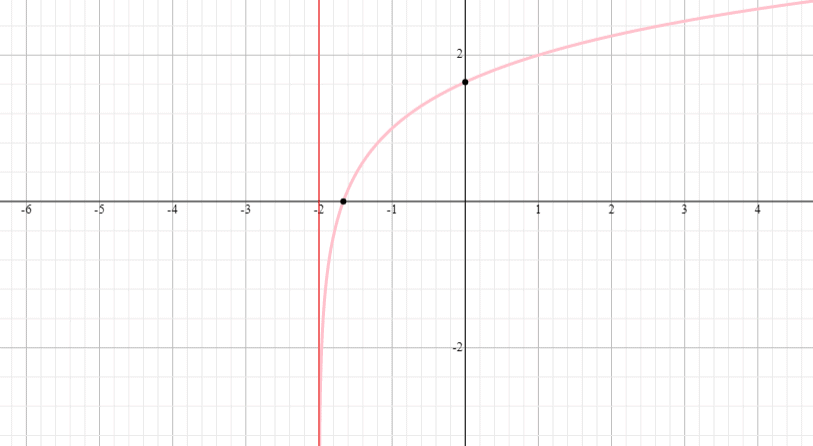
Teken een grafiek van de functie f(x) = log 2 (x + 1) en geef het domein en het bereik van de functie.
Oplossing
⟹ Domein: (- 1, oneindig)
⟹ Bereik: (-oneindig, oneindig)
Voorbeeld 4
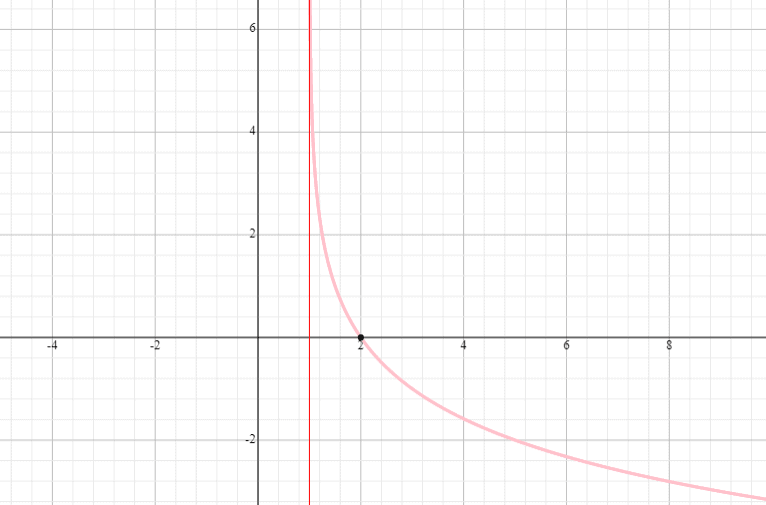
Grafiek y = log 0,5 (x – 1) en geef het domein en bereik op.
Oplossing
⟹ Domein: (1, oneindig)
⟹ Bereik: (-oneindig, oneindig)
Hoe grafisch een functie met een verticale verschuiving?
Een logaritmische functie met zowel horizontale als verticale verschuiving is van de vorm f(x) = log b (x) + k, waarbij k = de verticale verschuiving.
De verticale verschuiving beïnvloedt de eigenschappen van een functie als volgt:
- Het x-afsnijpunt zal met een vaste afstand van k omhoog of omlaag bewegen
Voorbeeld 5
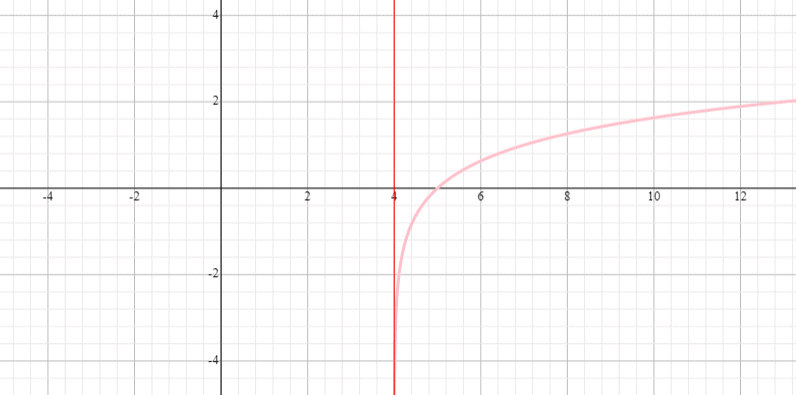
Grafeer de functie y = log 3 (x – 4) en geef het bereik en domein van de functie.
Oplossing
⟹ Domein: (0, oneindig)
⟹ Bereik: (-oneindig, oneindig)
Functies met zowel horizontale als verticale verschuiving
Een logaritmische functie met zowel horizontale als verticale verschuiving is van de vorm (x) = log b (x + h) + k, waarbij k en h respectievelijk de verticale en horizontale verschuiving zijn.
Voorbeeld 6
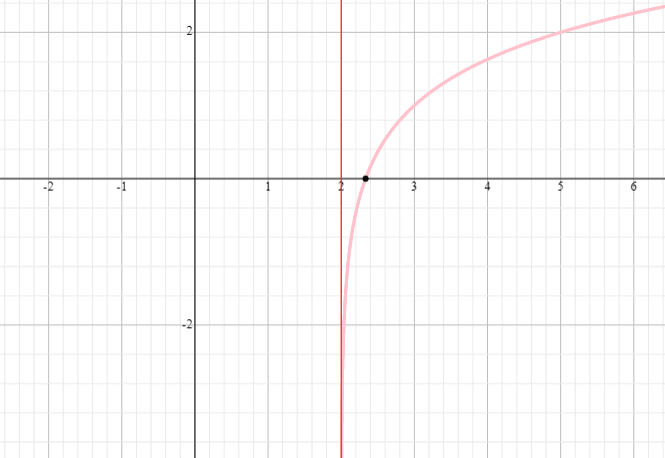
Grafeer de logaritmische functie y = log 3 (x – 2) + 1 en vind het domein en bereik van de functie.
Oplossing
⟹ Domein: (2,oneindig)
⟹ Bereik: (-oneindig, oneindig)
Voorbeeld 7
Grafeer de logaritmische functie y = log 3 (x + 2) + 1 en vind het domein en het bereik van de functie.
Oplossing
⟹ Domein: (- 2,oneindig)
⟹ Bereik: (-oneindig, oneindig)