Inleiding tot de Econometrie met R

Probit Regressie

In Probit regressie, wordt de cumulatieve standaardnormale verdelingsfunctie \(\Phi(\cdot)\) gebruikt om de regressiefunctie te modelleren wanneer de afhankelijke variabele binair is, dat wil zeggen dat we aannemen

(\beta_0 + \beta_1 X\) in (11.4) de rol speelt van een kwantiel \(z\). Bedenk dat de Probit-coëfficiënt \(\beta_1) in (11.4) de verandering in \(z) is die samenhangt met een verandering van één eenheid in \(X). Hoewel het effect van een verandering in \(X) op \(z) lineair is, is het verband tussen \(z) en de afhankelijke variabele \(Y) niet-lineair omdat \(psi) een niet-lineaire functie is van \(X).

Omdat de afhankelijke variabele een niet-lineaire functie is van de regressoren, heeft de coëfficiënt op \(X) geen eenvoudige interpretatie. Volgens sleutelbegrip 8.1 kan de verwachte verandering in de kans dat \(Y=1) als gevolg van een verandering in \(P/I verhouding) als volgt worden berekend:

1. Bereken de voorspelde kans dat \(Y=1) voor de oorspronkelijke waarde van \(X\).
2. Bereken de voorspelde kans dat \(Y=1) voor \(X + delta X).
3. Bereken het verschil tussen beide voorspelde kansen.

Natuurlijk kunnen we (11.4) veralgemenen naar Probit regressie met meerdere regressoren om het risico op bias door weggelaten variabelen te verkleinen. De essentie van Probit regressie is samengevat in Sleutelconcept 11.2.

We schatten nu een eenvoudig Probit-model van de kans op een hypotheekweigering.

# estimate the simple probit modeldenyprobit <- glm(deny ~ pirat, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Het geschatte model is

Net als in het lineaire waarschijnlijkheidsmodel vinden we dat de relatie tussen de kans op een afwijzing en de verhouding betalingen/inkomen positief is en dat de bijbehorende coëfficiënt zeer significant is.

De volgende codebrok reproduceert figuur 11.2 van het boek.

# plot dataplot(x = HMDA$pirat, y = HMDA$deny, main = "Probit Model of the Probability of Denial, Given P/I Ratio", xlab = "P/I ratio", ylab = "Deny", pch = 20, ylim = c(-0.4, 1.4), cex.main = 0.85)# add horizontal dashed lines and textabline(h = 1, lty = 2, col = "darkred")abline(h = 0, lty = 2, col = "darkred")text(2.5, 0.9, cex = 0.8, "Mortgage denied")text(2.5, -0.1, cex= 0.8, "Mortgage approved")# add estimated regression linex <- seq(0, 3, 0.01)y <- predict(denyprobit, list(pirat = x), type = "response")lines(x, y, lwd = 1.5, col = "steelblue")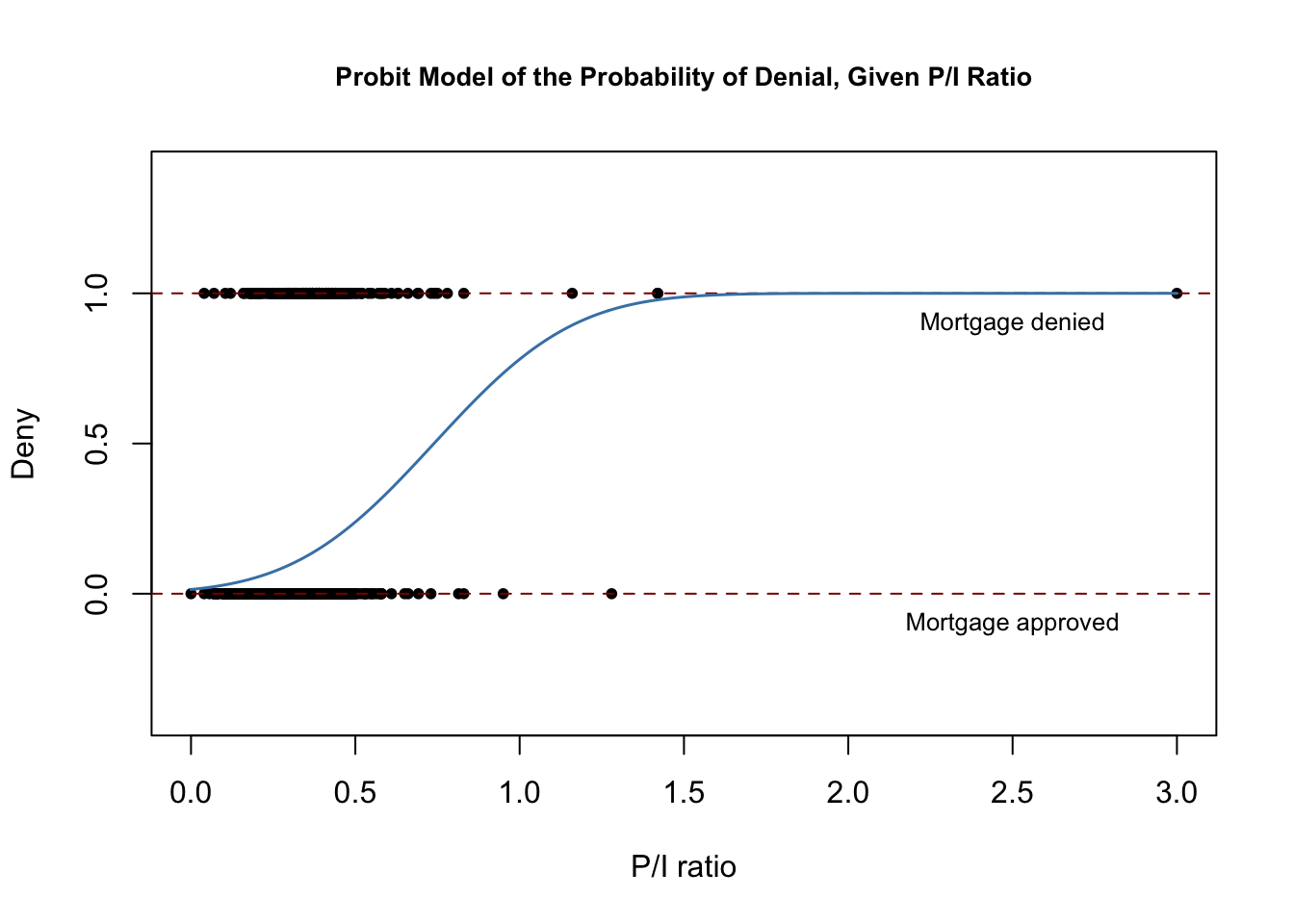

De geschatte regressiefunctie heeft een uitgerekte “S”-vorm die typerend is voor de CDF van een continue willekeurige variabele met symmetrische PDF zoals die van een normale willekeurige variabele. De functie is duidelijk niet-lineair en vlakt af voor grote en kleine waarden van de verhouding P/I. De functionele vorm zorgt er dus ook voor dat de voorspelde voorwaardelijke kansen op een weigering tussen 0 en 1 liggen.

We gebruiken voorspelling() om de voorspelde verandering in de weigeringskans te berekenen wanneer \(P/I \verhouding) wordt verhoogd van 0.

# 1. compute predictions for P/I ratio = 0.3, 0.4predictions <- predict(denyprobit, newdata = data.frame("pirat" = c(0.3, 0.4)), type = "response")# 2. Compute difference in probabilitiesdiff(predictions)#> 2 #> 0.06081433

We vinden dat een verhoging van de betalings-inkomensratio van 0,3 naar 0,4 volgens de voorspelling de kans op afwijzing met ongeveer 6,2% zal doen toenemen.

We gebruiken voorspellingen(() om de voorspelde verandering in de kans op afwijzing te berekenen wanneer de betalings-inkomensratio van 0,3 naar 0,4 wordt verhoogd.

We gaan verder met het gebruik van een vergroot Probit-model om het effect van ras op de kans op afwijzing van een hypotheekaanvraag te schatten.

denyprobit2 <- glm(deny ~ pirat + black, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De geschatte modelvergelijking is

Alle coëfficiënten zijn zeer significant, maar zowel de geschatte coëfficiënten voor de verhouding betalingen/inkomen als de indicator voor Afro-Amerikaanse afkomst zijn positief. Ook hier zijn de coëfficiënten moeilijk te interpreteren, maar zij wijzen erop dat, ten eerste, Afro-Amerikanen een grotere kans op afwijzing hebben dan blanke aanvragers, als we de verhouding betalingsverplichtingen/inkomen constant houden, en ten tweede, aanvragers met een hoge verhouding betalingsverplichtingen/inkomen een grotere kans lopen te worden afgewezen.

Hoe groot is het geschatte verschil in afwijzingskansen tussen twee hypothetische aanvragers met dezelfde verhouding betalingsverplichtingen/inkomen? Net als voorheen kunnen we predict() gebruiken om dit verschil te berekenen.

# 1. compute predictions for P/I ratio = 0.3predictions <- predict(denyprobit2, newdata = data.frame("black" = c("no", "yes"), "pirat" = c(0.3, 0.3)), type = "response")# 2. compute difference in probabilitiesdiff(predictions)#> 2 #> 0.1578117

In dit geval is het geschatte verschil in weigeringskansen ongeveer \(15,8%).