

Outliers Formula (Table of Contents)
- Outliers Formula
- Przykłady Outliers Formula (With Excel Template)
Outliers Formula
W statystyce, Outliers to dwa skrajnie odległe nietypowe punkty w danym zbiorze danych. Ekstremalnie wysokie wartości i ekstremalnie niskie wartości są wartościami odstającymi w zbiorze danych. Jest to bardzo przydatne w znalezieniu jakiejkolwiek wady lub błędu, który wystąpił. Po prostu, jak sama nazwa mówi, wartości odstające są wartościami, które leżą poza resztą wartości w zbiorze danych. Przykład, rozważ studentów inżynierii i wyobraź sobie, że mieli krasnoludki w swojej klasie. Tak więc krasnoludki to ludzie, którzy są wyjątkowo niskiego wzrostu w porównaniu z innymi ludźmi o normalnym wzroście. Jest to więc wartość odstająca w tej klasie. Wartości odstające mogą być obliczane przy użyciu metody Tukeya.
Start Your Free Investment Banking Course
Download Corporate Valuation, Bankowość inwestycyjna, Rachunkowość, Kalkulator CFA & inne
Wzór na wartości odstające –
Higher Outlier= Q3 + (1.5 * IQR)
Przykłady formuły Outliers (Z szablonem Excel)
Przyjrzyjrzyjmy się przykładowi, aby lepiej zrozumieć obliczanie formuły Outliers.
Outliers Formula – Example #1
Rozważmy następujący zestaw danych i obliczmy wartości odstające dla zestawu danych.
Zbiór danych = 5, 2, 7, 98, 309, 45, 34, 6, 56, 89, 23

Porządek rosnący zbioru danych:
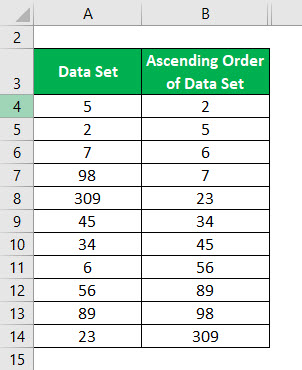

Medianę zbioru danych Ascending Order oblicza się jako:
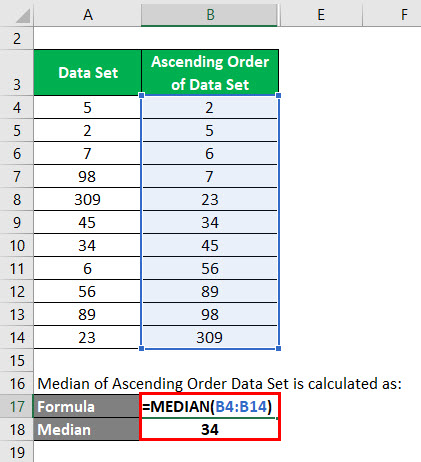

W tym zbiorze danych całkowita liczba danych wynosi 11. Zatem n= 11. Mediana = 11+1/2 = 12 / 2 = 6. Stąd wartość, która jest na 6 pozycji w tym zbiorze danych jest medianą.
Więc wartość mediany = 34.
Podziel zbiór danych na 2 połowy używając mediany.
4.9 (3,296 ratings)
View Course
Kurs Finanse dla menedżerów niefinansowych (7 kursów)
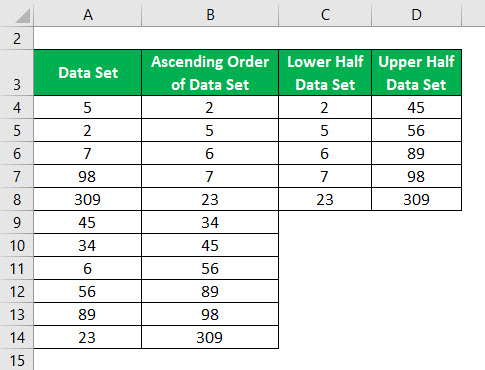

Medianę dolnej połowy i górnej połowy zbioru danych oblicza się jako:
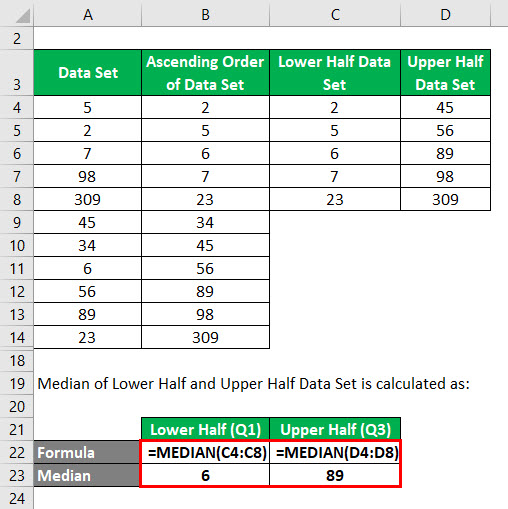

- W dolnej połowie 2, 5, 6,7,23, jeśli znajdziemy medianę tak jak w kroku 2, wartość mediany wyniesie 6. Więc Q1= 6.
- W górnej połowie 45, 56, 89, 98,309, jeśli znajdziemy medianę jak znaleźliśmy w kroku 2, wartość mediany będzie 89. Więc Q3= 89.
IQR jest obliczany przy użyciu wzoru podanego poniżej
IQR = Q3 – Q1
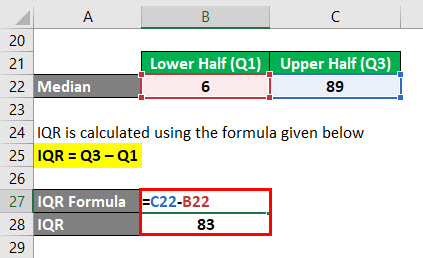

- IQR = 89 -.6
- IQR = 83
Lower Outlier jest obliczany za pomocą wzoru podanego poniżej
Lower Outlier = Q1 – (1.5 * IQR)
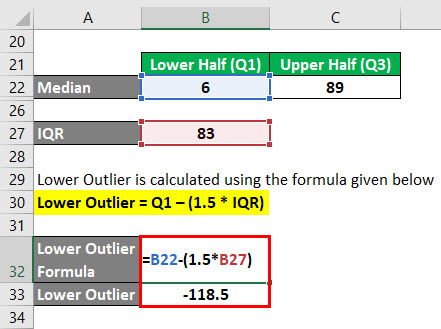

- Lower Outlier = 6 – (1.5 * 83)
- Lower Outlier = -118.5
Higher Outlier jest obliczany za pomocą wzoru podanego poniżej
Higher Outlier = Q3 + (1.5 * IQR)
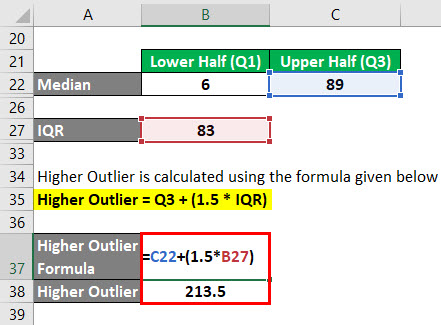

- Higher Outlier = 89 + (1.5 * 83)
- Higher Outlier = 213.5
Teraz pobierz te wartości w zbiorze danych -118.5, 2, 5, 6, 7, 23, 34, 45, 56, 89, 98, 213.5, 309. Wartości, które wypadają poniżej w dolnej stronie wartości i powyżej w wyższej stronie są wartością odstającą. Dla tego zestawu danych, 309 jest wartością odstającą.
Outliers Formula – Example #2
Rozważmy następujący zestaw danych i obliczmy wartości odstające dla zestawu danych.
Zestaw danych = 45, 21, 34, 90, 109.

Porządek rosnący zbioru danych:
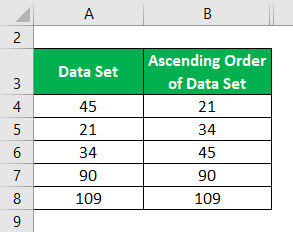

Medianę zbioru danych Ascending Order obliczamy jako:
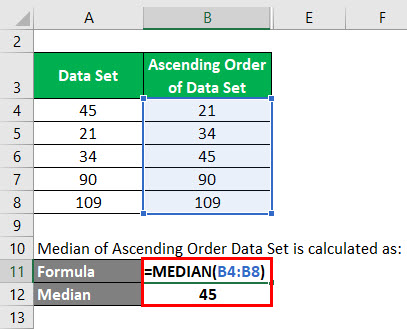

W tym zbiorze danych całkowita liczba danych wynosi 5. Zatem n = 5. Mediana = 5+1/2 = 6 / 2 = 3. Stąd wartość, która jest na 3 miejscu w tym zbiorze danych jest medianą.
Więc wartość mediany = 45.
Podziel zbiór danych na 2 połowy używając mediany.
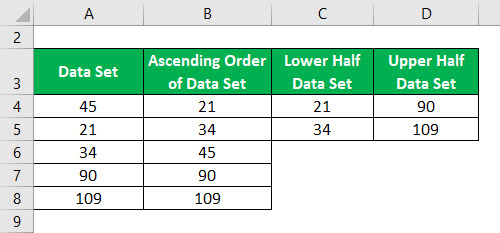

Mediana dolnej połowy i górnej połowy zbioru danych jest obliczana jako:
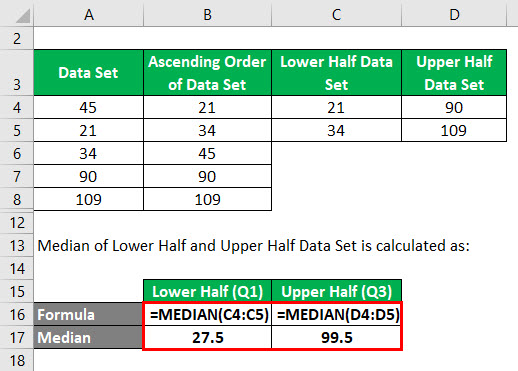

- Q1= 27.5
- Q3= 89
IQR oblicza się według wzoru podanego poniżej
IQR = Q3 – Q1
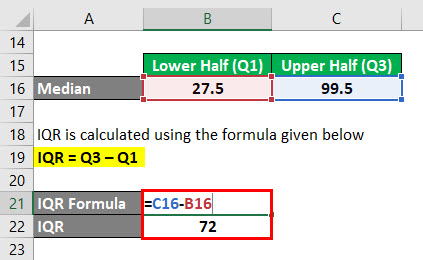

- IQR = 99.5 – 27.5
- IQR = 72
Lower Outlier jest obliczany za pomocą wzoru podanego poniżej
Lower Outlier = Q1 – (1.5 * IQR)
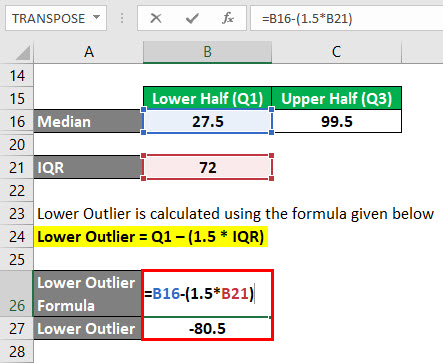

- Lower Outlier = 27.5 – (1.5 * 72)
- Lower Outlier = -80.5
Higher Outlier jest obliczany za pomocą wzoru podanego poniżej
Higher Outlier = Q3 + (1.5 * IQR)
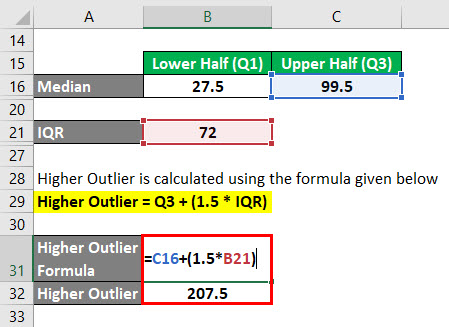

- Higher Outlier = 99.5 + (1.5 * 72)
- Higher Outlier = 207.5
Wyjaśnienie
Krok 1: Uporządkuj wszystkie wartości w danym zbiorze danych w kolejności rosnącej.
Krok 2: Znajdź wartość mediany dla danych, które są posortowane. Mediana może być znaleziona przy użyciu następującego wzoru. Poniższe obliczenie daje po prostu pozycję mediany wartości, która znajduje się w zestawie danych.
Mediana = (n+1)/2
Gdzie n jest całkowitą liczbą danych dostępnych w zestawie danych.
Krok 3: Znajdź dolny kwartyl wartości Q1 z zestawu danych. Aby ją znaleźć, użyj mediany, dzieląc zbiór danych na dwie połowy. Z dolnej połowy zestawu wartości, znajdź medianę dla tego dolnego zestawu, która jest wartością Q1.
Krok 4: Znajdź górny kwartyl wartości Q3 z zestawu danych. Jest to dokładnie taki sam krok jak powyższy. Zamiast dolnej połowy, musimy wykonać tę samą procedurę dla górnej połowy zestawu wartości.
Krok 5: Znajdź wartość Rozstępu Międzykwartylowego IQR. Aby znaleźć wartość IQR należy odjąć wartość Q1 od Q3.
IQR = Q3-Q1
Krok 6: Znajdź wartość wewnętrznego ekstremum. Koniec, który wypada poza dolną granicę, który może być również nazywany mniejszym odchyleniem. Mnożąc wartość IQR przez 1,5 i odejmując tę wartość od Q1 otrzymujemy Inner Lower Extreme.
Lower Outlier =Q1 – (1,5 * IQR)
Krok 7: Znajdź wartość Outer Extreme. Koniec, który wypada poza wyższą stronę, który może być również nazywany głównym odchyleniem. Pomnóż wartość IQR przez 1.5 i zsumuj tę wartość z Q3, co da ci Zewnętrzny Wyższy Ekstremum.
Wyższy Ekstremum = Q3 + (1.5 * IQR)
Krok 8: Wartości, które wypadają poza te wewnętrzne i zewnętrzne ekstrema są wartościami odstającymi dla danego zestawu danych.
Relevance and Uses of Outliers Formula
Outliers są bardzo ważne w każdym problemie analizy danych. Wartości odstające pokazują niespójność w dowolnym zbiorze danych, ponieważ są zdefiniowane jako niecodzienne, odległe od siebie wartości w zbiorze danych. Jest to bardzo przydatne w znalezieniu wszelkich wad, które wystąpiły w zestawie danych. Ponieważ, gdy umieścisz błąd w zestawie danych, wpływa on na średnią i medianę, stąd mogą pojawić się duże odchylenia w wyniku, jeśli wartości odstające są w zestawie danych. W związku z tym istotne jest, aby znaleźć Outliers z zestawu danych w celu uniknięcia poważnych problemów w analizie statystycznej.
Zalecane artykuły
To był przewodnik do formuły Outliers. Omawiamy tutaj sposób obliczania wartości odstających wraz z praktycznymi przykładami i szablonem Excela do pobrania. Możesz również zapoznać się z następującymi artykułami, aby dowiedzieć się więcej –
- Guide To Midrange Formula
- Examples of Salary Formula
- Calculator For DPMO Formula
- How To Calculate T Distribution?
- Quartile Deviation Formula | Examples