Cramers Rule with Two Variables

Cramer’s Rule é outro método que pode resolver sistemas de equações lineares usando determinantes.

Em termos de notações, uma matriz é um conjunto de números entre parênteses rectos enquanto que o determinante é um conjunto de números entre duas barras verticais.

Notações

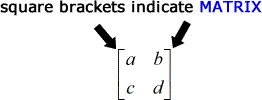
parênteses rectos indicam uma matriz, por exemplo

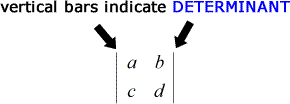
barras verticais (também conhecidas como "tubos") indicam um determinante de uma matriz, por exemplo, | a,b ; c,d ||"pipes") indicate a determinant of a matrix, for example, | a,b ; c,d |

A fórmula para encontrar o determinante de uma matriz 2 x 2 é muito simples.

Vamos fazer uma revisão rápida:

O determinante de uma Matriz 2 x 2

div>

Exemplos rápidos de como encontrar os determinantes de uma matriz 2 x 2

Exemplo 1: Encontrar o determinante da matriz A abaixo.

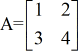
Matriz A é uma matriz quadrada 2x2 com elementos 1 e 2 na sua primeira fila, e elementos 3 e 4 na sua segunda fila. Em alternativa, podemos escrever a matriz A como A = .

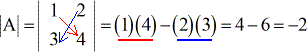
O determinante da matriz A que pode ser escrita como det = |A| = |1,2;3,4| = (1)(4) - (2)(3) = 4-6 = -2. Portanto, o determinante da matriz A é negativo 2.

Exemplo 2: Encontrar o determinante da matriz B abaixo.

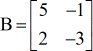
Matriz B é uma matriz de 2 por 2 quadrados com as entradas 5 e -1 na primeira linha, e as entradas 2 e -3 na segunda linha. Esta matriz pode ser expressa como B=.

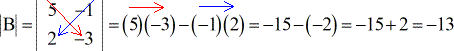
O determinante da matriz B que pode ser escrita como det = |B| = |5,-1;2,-3| = (5)(-3) - (-1)(2) = -15-(-2) = -15 + 2 = -13. Isso torna o determinante da matriz B negativo 13.

Exemplo 3: Encontrar o determinante da matriz C abaixo.

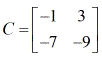
Matriz C é uma matriz quadrada com duas filas e duas colunas. Os elementos da primeira fila são -1 e 3 enquanto os elementos da segunda fila são -7 e -9. Assim, a matriz C = .

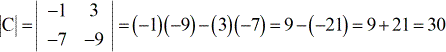
O determinante da matriz C que pode ser escrita como det = |C| = |-1,3;-7,-9| = (-1)(-9) - (3)(-7) = 9+21 = -15 + 2 = 30. Assim, o determinante da matriz C é positivo 30.

Após saber como encontrar o determinante de uma matriz 2 x 2, está agora pronto para aprender os procedimentos ou passos sobre como usar a Regra de Cramer. Aqui vamos nós!

Regra de Cramer para Sistemas de Equações Lineares com Duas Variáveis

Dado um sistema linear

Este é um diagrama que mostra um sistema de equações lineares onde a primeira equação linear é a1x+b1y=c1 enquanto a segunda é a2x+b2y=c2. A x-cloumn (também conhecida como primeira coluna) inclui as constantes ligadas à variável x, a coluna y (também conhecida como segunda coluna) inclui as constantes ligadas à variável y, e finalmente a coluna constante (também conhecida como terceira coluna) inclui apenas as constantes, ou seja, apenas constantes sem quaisquer variáveis ligadas a elas.

Atribuir nomes para cada matriz

matriz eficiente:

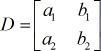
Matriz D é também conhecida como a "matriz de coeficiente" com entradas a1 e b1 na primeira linha, e entradas a2 e b2 na segunda linha. Podemos escrever isto como matriz de coeficiente D = ."coefficient matrix" with entries a1 and b1 on the first row, and entries a2 and b2 on the second row. We can write this as coefficient matrix D = .

X – matriz:

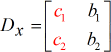
Y – matriz:

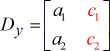
Matriz Dy (lido como "D subscript y") também é conhecida como "y-matrix" com elementos a1 e c1 na primeira linha, e elementos a2 e c2 na segunda linha. Isto pode ser escrito como, y-matrix, Dy = ."D subscript y") is also known as the "y-matrix" with elements a1 and c1 on the first row, and elements a2 and c2 on the second row. This can be written as, y-matrix, Dy = .

para resolver para a variável x.

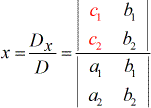
Para resolver para x, a fórmula é, x = Dx/D = (determinante da matriz x) dividido por (determinante da matriz do coeficiente) = |c1,b1;c2,b2| / |a1,b1;a2,b2|.

para resolver para a variável y.

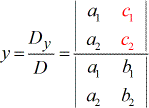
Para resolver para y, a fórmula é, y = Dy/D = (determinante da matriz y) dividida por (determinante da matriz de coeficiente) = |a1,c1;a2,c2| / |a1,b1;a2,b2|.

Poucos pontos a considerar quando se olha para a fórmula:

1) As colunas de \máximo{x}, \máximo{y}, e os termos constantes \máximo{c} são obtidos da seguinte forma

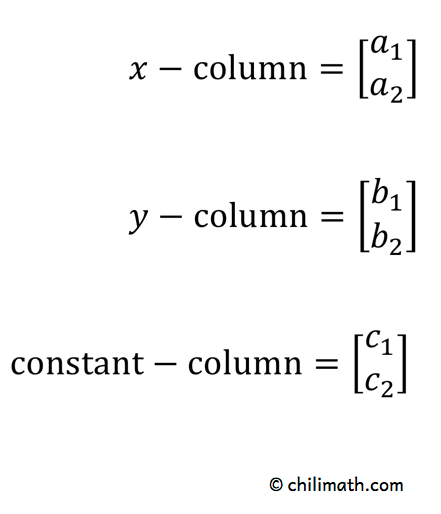
2x1 matrizes de colunas x, y e constante

2) Ambos os denominadores na resolução de \i1 e \i1 são os mesmos. Vêm das colunas de {x} e {y}largura{x}.

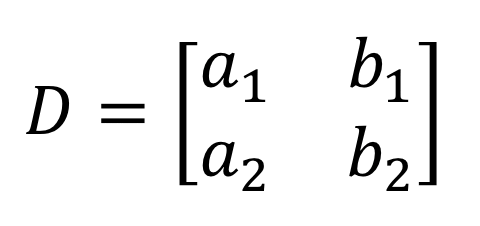
3) Olhando para o numerador na resolução para \i1{x}largura, os coeficientes da coluna da \i1{x}largura são substituídos pela coluna da constante (a vermelho).

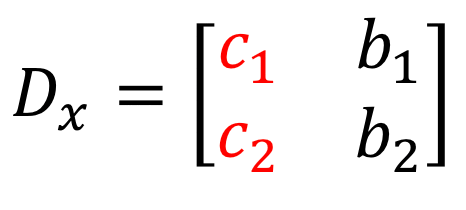
4) Da mesma forma, para resolver para \larga, os coeficientes da coluna de \larga são substituídos pela coluna constante (a vermelho).

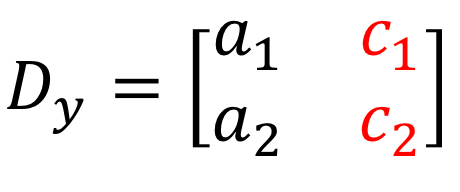
Exemplos de Como Resolver Sistemas de Equações Lineares com Duas Variáveis usando a Regra de Cramer

Exemplo 1: Resolva o sistema com duas variáveis pela Regra de Cramer

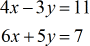
os sistemas de equações com duas variáveis são 4x-3y=11 e 6x+5y=7

Inicie extraindo as três matrizes relevantes: coeficiente, {x}, e {y}large{x}, e {y}large{y}. Em seguida, resolver cada determinante correspondente.

Para matriz de coeficiente

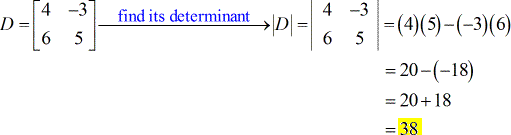
Solva para o determinante da matriz de coeficiente D com os elementos 4 e -3 na primeira linha, e os elementos 6 e 5 na segunda linha. O determinante da matriz D = = |D| = |4,-3;6,5| = (4)(5) - (-3)(6) = 20 - (-18) = 20 + 18 = 38.

Para X – matriz

Solva para o determinante do subscrito x-matriz D com os elementos 11 e -3 na primeira linha, e os elementos 7 e 5 na segunda linha. O determinante da matriz Dx = = |Dx| = |11,-3;7,5| = (11)(5) - (-3)(7) = 55 - (-21) = 55 + 21 = 76.

Para Y – matriz

Solva para o determinante do subscrito y-matriz D com os elementos 4 e 11 na primeira linha, e os elementos 6 e 7 na segunda linha. O determinante da matriz Dy = = | |Dx| = |4,11;6,7| = (4)(7) - (11)(6) = 28 - (66) = -38.

Após todos os três determinantes serem calculados, é altura de resolver para os valores de \large{x} e \large{y} usando a fórmula acima.

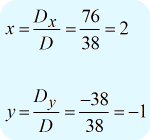
Para resolver para x, temos x = Dx/D = 76/38 = 2, e para y, temos y = Dy/D = -38/38 = -1.

Posso escrever a resposta final como \large{\i1}left( {x,y} {x,right) = \i}left( {2, – 1} {\i} right)}.

Exemplo 2: Resolver o sistema com duas variáveis por Cramer’s Rule

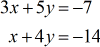
os sistemas de equações com duas variáveis (nomeadamente, x e y) são 3x+5y=-7 e x+4y=-14

Configure o seu coeficiente, {x}, e {y} aumente as matrizes do sistema de equações lineares dado. Em seguida, calcular os seus determinantes em conformidade.

Lembrar que subtraímos sempre os produtos das entradas diagonais.

Para a matriz de coeficiente (usar os coeficientes de ambas as variáveis x e y)

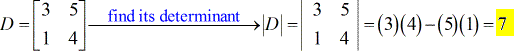
Solver o determinante da matriz de coeficiente D com as entradas 3 e 5 na primeira linha, e as entradas 1 e 4 na segunda linha. O determinante da matriz D = = |D| = |3,5;1,4| = (3)(4) - (5)(1) = 12 - (5) = 12 - 5 = 7.

Para a matriz X – (substituir a coluna x pela coluna constante)

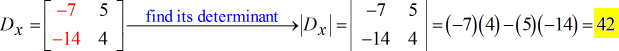
Solver o determinante da matriz x, também conhecido como D subscrito x, com entradas -7 e 5 na primeira linha, e entradas -14 e 4 na segunda linha. O determinante da matriz Dx = = |D| = |-7,5;-14,4| = (-7)(4) - (5)(-14) = -28 - (-70) = -28 + 70 = 42.

Para a matriz Y – (substituir a coluna y pela coluna constante)

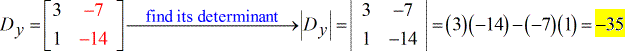
Solver o determinante da matriz y, também conhecido como D subscript y, com as entradas 3 e -7 na primeira linha, e as entradas 1 e -14 na segunda linha. O determinante da matriz Dy = = |D| = |3,-7;1,-14| = (3)(-14) - (-7)(1) = -42 - (-7) = -42 + 7 = -35.

Espero que esteja a obter computação confortável para o determinante de uma matriz bidimensional. Para finalmente resolver as variáveis necessárias, obtenho os seguintes resultados…

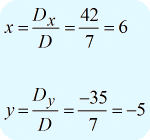
Para resolver para x, dividimos o determinante da matriz x pelo determinante da matriz de coeficiente. Da mesma forma, para resolver para y, dividimos o determinante da matriz y pelo determinante da matriz do coeficiente. Portanto, x = Dx/D = 42/7 = 6; y = Dy/D = -35/7 = -5. Assim, a resposta final é (x,y) = (6,-5).

Escrevendo a resposta final na notação de ponto, obtive {\i1}largura( {x,y} {\i} {\i} = {\i}esquerda( {6, – 5} {\i} {\i} {\i} {\i}.

Exemplo 3: Resolver o sistema com duas variáveis pela Regra de Cramer

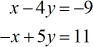
Este problema pode de facto ser resolvido com bastante facilidade pelo Método de Eliminação. Isto porque os coeficientes da variável x são os “mesmos” mas apenas opostos em sinais ( +1 e -1 ). Para resolver isto utilizando o método de eliminação, adicionam-se as suas colunas correspondentes e a variável x desaparece – deixando-o com uma equação de um passo em \large{y}. Menciono isto porque cada técnica tem falhas e é melhor escolher a mais eficiente. Esclareça sempre com o seu professor se não há problema em utilizar outra abordagem quando o método não é especificado num determinado problema.

Anyway, uma vez que estamos a aprender a resolver pela Regra de Cramer, vamos em frente e trabalhar com este método.

Eu construirei três matrizes ( coeficiente, \x e \x) e avaliarei os seus correspondentes determinantes.

Para a matriz do coeficiente

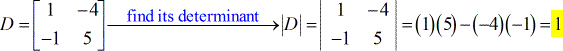
Para a matriz do coeficiente D = , o seu determinante é resolvido da seguinte forma: |D| = |1,-4;-1,5| = (1)(5) - (-4)(-1) = 5 - (4) = 1. Assim, |D| = 1.

Para X – matriz ( escrita como letra maiúscula D com subscrito x )

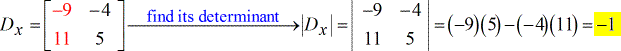
Para a matriz x Dx = , o seu determinante é resolvido da seguinte forma: |Dx| = |-9,-4;11,5| = (-9)(5) - (-4)(11) = -45 - (-44) = -45 + 44 = -1. Assim, |Dx| = -1.

Para Y – matriz (escrita como maiúscula D com subscrito y)

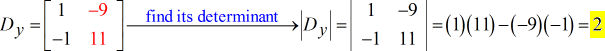
Para a matriz y Dy = , o seu determinante é resolvido da seguinte forma: |Dy| = |1,-9;-1,11| = (1)(11) - (-9)(-1) = 11 - (9) = 11 - 9 = 2. Assim, |Dy| = 2.

Após a obtenção dos valores dos três determinantes requeridos, calcularei \i1{x} e \i1{y} como se segue.

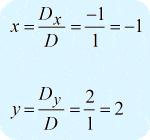
Solvendo o valor de x, dividir o determinante da matriz x pelo determinante da matriz de coeficiente. Da mesma forma, para resolver para y, dividir o determinante da matriz y pelo determinante da matriz do coeficiente. Assim, x = Dx/D = -1/1 = -1; y = Dy/D = 2/1 = 2. Assim, a resposta final é (x,y) = (-1,2).

A resposta final na forma de ponto é \larga (esquerda( {x,y} {x,y} {direita) = \querda( { – 1,2} {direita)} .

Exemplo 4: Resolva pela Regra de Cramer o sistema com duas variáveis

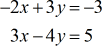
o sistema de equações lineares com duas variáveis são -2x+3y=-3 e 3x-4y=5

P>Desde que já revimos alguns exemplos, Sugiro que tente este problema por si próprio. Depois, compare as suas respostas com a solução abaixo.

Se acertar na primeira vez, isso significa que se está a tornar um “profissional” no que diz respeito à Regra de Cramer. Se não o fez, tente descobrir o que correu mal e aprenda a não cometer o mesmo erro da próxima vez. É assim que se torna melhor a matemática. Estude muitos tipos de problemas e, mais importante ainda, faça muitas práticas independentes.

Para matriz de coeficiente

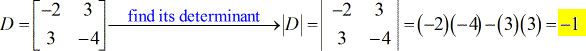
Solver para a matriz de coeficiente D, temos D = , os passos para resolver o seu determinante é |D| = |-2,3;3,-4| = (-2)(-4) - (3)(3) = 8 - (9) = -1. E assim, |D| = -1.

Para X – matriz

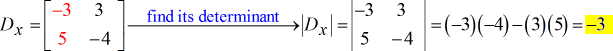
Solver para a matriz x Dx, temos Dx= , os passos para resolver o seu determinante é |Dx| = |-3,3;5,-4| = (-3)(-4) - (3)(5) = 12 - (15) = -3. E assim, |Dx| = -3.

Para Y – matriz

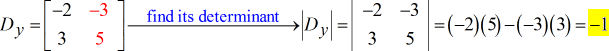
Solve para a matriz y Dy, temos Dy = , os passos para resolver o seu determinante é |Dy| = |-2,-3;3,5| = (-2)(5) - (-3)(3) = -10 - (-9) = -10 + 9 = -1. Isso faz, |Dy| = -1.

Deverá obter a resposta abaixo…

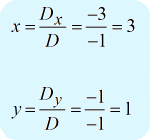
Para resolver para o x, temos x = Dx/D = -3/-1 = 3. Portanto, x é igual a 3. A seguir, para resolver para y, mostramos que y = Dy/D = -1/-1 =1. Portanto, y é igual a 1.

Exemplo 5: Resolver o sistema com duas variáveis pela Regra de Cramer

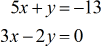
os sistemas de equações lineares a resolver são os seguintes: 5x+y=-13, 3x-2y=0

Para o nosso último exemplo, incluí um zero na coluna constante. Sempre que se vê o número zero na coluna constante, recomendo vivamente a utilização da Regra de Cramer para resolver o sistema de equações lineares. Porquê? Porque o cálculo dos determinantes das matrizes {x} e \i1}grande{y} se tornam drasticamente super fáceis. Confira você mesmo!

Para matriz de coeficiente

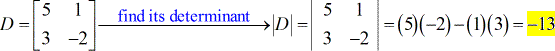
O determinante do coeficiente D = é resolvido como |D| = |5,1;3,-2| = (5)(-2) - (1)(3) = -13.

Para X – matriz

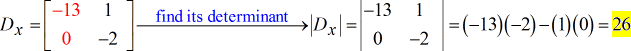
O determinante da matriz x Dx = é resolvido como |Dx| = |-13,1;0,-2| = (-13)(-2) - (1)(0) = 26.

For Y – matrix

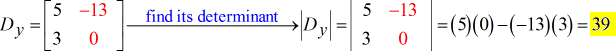
O determinante do y-matrix Dy = é resolvido como |Dy| = |5,-13;3,0| = (5)(0) - (-13)(3) = 0 + 39 = 39.

A solução final para este problema é

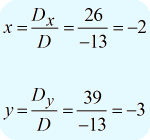
Para resolver x, dividimos x-matriz por matriz de coeficiente que nos dá x = Dx/D = 26/-13 = -2. Para resolver y, dividimos a matriz y por matriz de coeficiente que nos dá y = Dy/D = 39/-13 = -3.

Prática com folhas de trabalho

P>Pode também estar interessado em:

Regra do Cramer 3×3

Cramer’s Rule for a 2×2 System (with Two Variables)