Pés de superfície por minuto, carga de cavacos, espessura de cavacos não conformados e desbaste de cavacos são termos de loja familiares. Nas últimas semanas, no entanto, várias ocorrências na nossa loja fizeram-me perceber que há muitos profissionais da metalomecânica que não compreendem estes termos e os cálculos que os acompanham. Quer se trabalhe numa loja de pequenos trabalhos ou num grande fabricante contratado, é importante compreender os cálculos das ferramentas de corte e como utilizá-las para ajudar a obter ganhos de eficiência significativos.
Os cálculos da velocidade de corte podem muito bem ser os mais importantes. São fáceis de utilizar e, com uma pequena explicação, fáceis de compreender. A velocidade de corte de uma ferramenta é expressa em pés de superfície por minuto (sfm) ou metros de superfície por minuto (m/min.). Semelhante ao mph para um carro, sfm é a distância linear que uma ferramenta de corte percorre por minuto. Para se obter um sentido de escala mais apostado, 300 sfm, por exemplo, converte para 3,4 mph.
Ferramentas recomendam velocidades de corte para diferentes tipos de materiais de peças de trabalho. Quando um fabricante de ferramentas sugere 100 sfm, está a indicar que a superfície exterior da ferramenta rotativa deve viajar a uma velocidade igual a 100 pés lineares por minuto. Se a ferramenta tiver uma circunferência (diâmetro × π) de 12″, teria de rodar a 100 rpm para atingir 100 sfm.
Todas as imagens cortesia de C. Tate
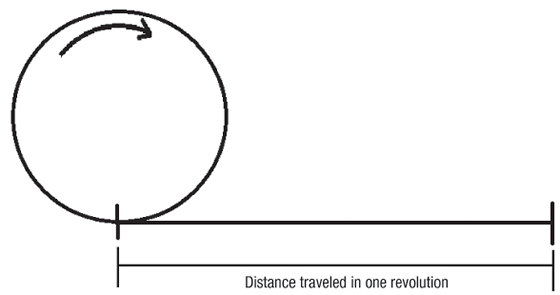
Imagine a ferramenta de corte como um anel ou cilindro rolante. A distância percorrida em uma rotação vezes rpm é a sua velocidade superficial. Se o círculo acima tivesse um diâmetro de 3,82″, a circunferência seria de 12″. Como resultado, cada volta produziria uma distância linear de 1′, e uma velocidade do fuso de 100 rpm seria uma velocidade de corte de 100 sfm.
A seguinte equação é usada para calcular a velocidade do fuso: rpm = sfm ÷ diame-ter × 3,82, onde diâmetro é o diâmetro da ferramenta de corte ou o diâmetro da peça num torno em polegadas, e 3.82 é uma constante que vem de uma simplifica-ção algébrica da fórmula mais complexa: rpm = (sfm × 12) ÷ (diâmetro × π).
Porque o diâmetro da ferramenta é medido em polegadas, os “pés” em sfm devem ser con-vertidos em polegadas, e porque há 12 polegadas num pé, multiplicar sfm por 12. Além disso, a circunferência da ferramenta é encontrada multiplicando o diametro da ferramenta por π, ou 3,14 para simplificar. O resultado é: rpm = (sfm × 12) ÷ (diâmetro × π) = (sfm ÷ diâmetro) × (12 ÷ π) = (sfm ÷ di-ametro) × 3,82.

Nota as linhas verticais, chamadas marcas de ferramentas, no exterior da peça a ser rodada. À medida que a taxa de avanço aumenta, a distância entre as linhas também aumenta. A espessura da apara é aproximadamente igual à do avanço.
As velocidades de corte são publicadas em sfm porque a velocidade de corte ideal para uma família par-ticular de ferramentas será, em teoria, a mesma, independentemente do tamanho da ferramenta. Espera-se que o engenheiro, programador ou maquinista calcule as rpm necessárias para produzir a velocidade de corte adequada para cada ferramenta seleccionada.
Então o que é que isto nos diz? Digamos que uma ferramenta de 1″-dia. deve funcionar a 100 sfm. Com base na equação, essa ferramenta deve rodar a 382 rpm para atingir 100 sfm: 100 ÷ 1 × 3,82 = 382,
Outra forma de considerar este conceito é pensar na distância que a ferramenta de 1″ percorreria se fizesse 382 revo-luções através do chão de fábrica. Nesse sce-nario, viajaria 100′; fá-lo-ia em 60 segundos e estaria a viajar 100 sfm.
Tornos são diferentes, claro, por causa da rotação da peça em vez da ferramenta de corte. Como a fórmula para a velocidade de corte depende do diâmetro, à medida que o diâmetro da peça diminui, as rpm devem aumentar para manter uma velocidade de superfície con-stant. Após cada corte circular no torno, o diâmetro externo da peça diminui ou o ID aumenta, e é necessário que as rpm da peça aumentem para manter a velocidade de corte desejada. Como resultado, os fabricantes CNC desenvolveram a função de filmagens de superfície constante para os controlos do torno. Esta característica permite ao programador introduzir a velocidade de corte desejada em sfm ou m/min. e o controlo calcula as rpm adequadas para o diâmetro de corte.
Enquanto a ferramenta ou peça estiver a rodar, a máquina deve saber a velocidade de deslocação enquanto a fresa está engatada na peça. Taxa de avanço é o termo que descreve a taxa de avanço enquanto se corta.
A taxa de avanço para fresagem é normalmente expressa em polegadas por minuto (ipm) e calculada utilizando: ipm = rpm × nº de flautas × carga de cavacos.
O que é a carga de cavacos? Na fresagem, é a quantidade de material que a aresta de corte retira cada vez que roda. Ao rodar, é a distância que a peça se desloca numa volta enquanto está engatada com a ferramenta. É por vezes referida como espessura da apara, o que é uma espécie de verdade. A espessura da apara pode mudar quando outros parâmetros como o DOC radial ou o ângulo de chumbo da ferramenta mudam.
Os fabricantes de ferramentas publicam recomendações de carga de apara juntamente com recomendações de velocidade de corte e expressam-nas em milésimos de polegada (milímetro para unidades métricas). Para operações de fresagem e perfuração, a carga de apara é expressa em milésimos de polegada por flauta. Flautas, dentes e arestas de corte descrevem todas a mesma coisa e deve haver pelo menos uma, mas, em teoria, não há limite para o número que uma ferramenta pode ter.
As recomendações de carga de chip para operações de torneamento são na maioria das vezes dadas em milésimos de polegada por revolução, ou alimentação por rotação. Esta é a distância que a ferramenta avança cada vez que a peça faz uma rotação.
Que rpm e taxa de alimentação deve ser programada para uma fresa de 4 canais, de 1″, funcionando a uma velocidade de corte recomendada de 350 sfm e uma carga de cavacos recomendada de 0,005 polegadas por dente (ipt)? Usando a equação, rpm = sfm ÷ diâmetro × 3,82 = 350 ÷ 1,0 × 3,82 = 1,337, a taxa de alimentação = rpm × n.º de flautas × carga de cavacos = 1,337 × 4 × 0,005 = 26,74 ipm.
Aqui é onde as coisas se tornam interessantes, porque ao alterar os valores na fórmula, as relações das diferentes variáveis tornam-se evidentes. Tente aplicar uma ferramenta de 2″ em vez da ferramenta de 1″. O que acontece? As rpm e a taxa de alimentação diminuem para metade.
A compreensão destas relações e a aplicação de algum pensamento criativo pode favorecer ganhos significativos de eficiência. Discutirei como tirar partido destas relações na minha próxima coluna. CTE
Sobre o Autor: Christopher Tate é engenheiro de fabrico avançado sénior da Milwaukee Electric Tool Corp., Brookfield, Wis. Ele está baseado na fábrica da empresa em Jackson, Miss. Tem 19 anos de experiência na indústria metalúrgica e possui um Mestrado e Bacharelato em Ciências pela Universidade Estatal do Mississippi. E-mail: [email protected].