Introdução
Propriedades elásticas desempenham um papel importante em vários processos de membrana, como por exemplo, fusão de membranas (Chernomordik e Kozlov, 2008) e modulações de actividades de canal de membrana (Schmidt e MacKinnon, 2008); Sansom e Biggin, 2010; Mashaghi et al., 2013b). Nas células, as membranas exteriores são suportadas pelas redes de actina subjacentes. A tensão mecânica é então dominada pelo citoesqueleto de actina associado em escalas de comprimento superiores à malha da rede de actina (30-300 nm) (Morone et al., 2006). Em pequenas escalas de comprimento, no entanto, a contribuição do bico lipídico dominará. Como tal, foram feitos esforços para estudar as propriedades mecânicas das manchas de bocal com dimensões próximas da dimensão da malha do citoesqueleto de actina (Claesson et al., 2011).
Ao considerar uma membrana como um corpo bidimensional, ou seja, negligenciando a sua espessura, as suas propriedades mecânicas na ausência de anisotropia podem ser caracterizadas por duas constantes elásticas de acordo com a teoria da elasticidade contínua. Na prática comum de caracterização de materiais, estes parâmetros são tipicamente o módulo de Young e o rácio de Poisson. As estimativas para o módulo de membranas de Young foram fornecidas por experiências (Tierney et al., 2005; Popescu et al., 2006). Contudo, a medição da razão de Poisson não é simples, devido à pequena espessura das membranas na gama de nanómetros (Mitchell et al., 2003; Martins et al., 2009). Do aspecto teórico, as propriedades mecânicas das membranas lipídicas são normalmente investigadas com base no Helfrich Hamiltonian. A principal quantidade física obtida de tais estudos é a rigidez à flexão. O módulo de Young e o rácio de Poisson estão inter-relacionados por fórmula que incorpora a rigidez à flexão, mas nem o módulo de Young nem o rácio de Poisson foram determinados separadamente até agora.
Simulações e modelos teóricos foram utilizados para fornecer informação importante sobre elasticidade (Goetz e Lipowsky, 1998; Lindahl e Edholm, 2001; Ayton et al., 2002) e propriedades viscosas dos bílis lipídicos (Jeon e Voth, 2005). A investigação das propriedades mecânicas das películas finas não se limita às biomembranas e representa uma área activa de investigação na ciência dos materiais. Foram feitos esforços para prever a relação de Poisson de filmes feitos de vários materiais por meio de simulações computorizadas. Por exemplo, Galvao et al. utilizaram simulações de dinâmica molecular utilizando potenciais de ordem empírica reactiva para investigar as propriedades mecânicas dos nanoribões de grafeno (Martins e Galvao, 2010). Baughman et al. propuseram um modelo para estimar a razão de Poisson de redes de fibras e aplicaram-no com sucesso a folhas de nanotubos de carbono (papel de fivela) (Hall et al., 2008).
Neste trabalho, introduzimos um método para determinar a razão de Poisson ν em simulações e aplicamo-lo ao modelo de membrana lipídica de grãos grossos, que foi introduzido por Lenz e Schmid (2005). Este método é geral e aplicável a quaisquer outras superfícies. Após determinar a rigidez de flexão kc a partir do espectro de potência das flutuações de altura da membrana, podemos calcular o módulo de Young E.
Materiais e Métodos
Monte Carlo foram realizadas simulações de balizas lipídicas com condições periódicas de contorno em direcções laterais para o modelo de grãos grossos introduzido por Lenz e Schmid (2005). Neste modelo, são consideradas as ampolas de cauda única, que são representadas por seis contas de cauda e uma conta de cabeça ligeiramente maior (com uma razão de tamanho de 1-1,1). Contas pertencentes a uma molécula são ligadas através de molas elásticas não lineares (FENE) finamente extensíveis (Grest e Kremer, 1986) com um potencial de estiramento de ligação Figura 1:

Figure 1. Interacções aplicadas no modelo.
Here r é a distância entre contas adjacentes, νFENE caracteriza a força da mola, r0 é o comprimento óptimo da ligação (sem estiramento), e Δrm é a distância máxima de estiramento. A rigidez das caudas é tida em conta por um potencial de ângulo ósseo harmónico
onde θijk é o ângulo ósseo associado a três contas adjacentes. Tanto os grânulos não ligados pertencentes à mesma molécula como os grânulos pertencentes a moléculas diferentes interagem através de um potencial de núcleo mole:
where θ(.) é a função de passo Heaviside. As moléculas de solvente são representadas por um modelo fantasma de esferas que interagem com as esferas lipídicas via VSC(r) (com os mesmos parâmetros que as esferas da cabeça) mas não interagem com elas próprias. Todos os parâmetros do modelo foram escolhidos de acordo com o modelo referenciado (Lenz e Schmid, 2005) e estão resumidos na Tabela 1.

Tabela 1. Os potenciais de interacção do modelo referenciado e os parâmetros correspondentes.
Biletes lípidos exibem um rico espectro de estruturas e transições de fase (Nagle e Tristram-Nagle, 2000; Illya et al., 2005; Seto et al., 2008; Thakkar et al., 2011). O estado fluido a altas temperaturas é caracterizado por uma disposição desordenada das caudas lipídicas e uma mobilidade lipídica comparativamente elevada. Ao arrefecer, este estado fluido sofre uma transição de fase para um estado de gel, onde as moléculas lipídicas são mais ordenadas e têm uma mobilidade mais baixa. Outras fases possíveis são a fase interdigitada, na qual as caudas lipídicas de monocamadas opostas se interpenetram.
Ao digitalizar o diagrama de fases do modelo referenciado (Lenz, 2007), em primeiro lugar equilibrámos as camadas lipídicas em cerca de dois milhões de passos de Monte Carlo (MC) para produzir fases diferentes para o objectivo deste trabalho, ver Figura 2. Nas unidades reduzidas, ϵ/kB para a temperatura T e σLJ3/σLJ3 para a pressão P, são as variáveis termodinâmicas correspondentes: P = 2 e T = 1,08 para a fase de gel, P = 1 e T = 1,3 para a fase de fluido, P = 0,5 e T = 1,16 para a fase interdigitada. Os parâmetros característicos para diferentes fases incluindo o comprimento médio da cadeia l¯, espessura do bico d, área por lipídio A, e parâmetro de ordem da cadeia Sz estão resumidos na Tabela 2.

Figura 2. Instantâneos da membrana lipídica simulada no (A) gel, (B) fluido, e (C) fase interdigitada. As contas da cabeça e da cauda dos lípidos são mostradas em vermelho e verde, respectivamente.
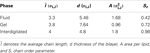
Tabela 2. Parâmetros característicos dos bicos lipídicos.
Simulações foram realizadas sob condições de temperatura e pressão constantes (conjunto NPT) para bicos lipídicos com tamanhos diferentes. Para investigar o espectro de potência das flutuações de altura das superfícies, simulámos um bocal cujos folhetos superiores e inferiores consistem em 64 × 64 moléculas de lípidos. Cerca de 17000-72000 esférulas foram escolhidas para o modelo solvente (o número preciso depende da fase simulada). Para realizar a análise da razão de Poisson, equilibramos biletes rectangulares constituídos por 12 × 24 moléculas lipídicas por folheto para três fases diferentes.
Para determinar tanto E como ν, precisamos de determinar uma destas constantes elásticas separadamente. Utilizando as condições de contorno periódicas, introduzimos um método para calcular a razão de Poisson para a superfície (Abedpour et al., 2010). A razão de Poisson é a razão negativa das alterações de tensão transversal dividida pelas alterações de tensão axial num corpo quando este é esticado ou comprimido na direcção axial sob a tensão abaixo do limite proporcional. Para as deformações diagonais infinitesimais, a razão de Poisson pode ser substituída pela razão das alterações do comprimento relativo como νij = -ΔLi/ηjLi, onde ηj ≡ ΔLi/Lj é definido como a fracção da alteração do comprimento axial. Aqui i ≠ j e i = x, y, e z. No método, apresentamos aqui o comprimento entre lípidos vizinhos é redimensionado por um factor de (1 + η) na direcção axial, digamos y-direcção, e a subsequente alteração do tamanho da caixa de simulação nas direcções perpendiculares, neste caso x- e z-direcção, são monitorizados. Embora mantendo constante o comprimento da caixa redimensionada (1 + η) Ly, para fixar a pressão nas simulações, as dimensões da caixa podem agora flutuar apenas nas direcções x e z. Quando os comprimentos médios iniciais em x e z-direcções eram Lx e Lz, novos valores médios de Lx + ΔLx e Lz + ΔLz são atingidos após a redimensionamentação, re-equilibrando o sistema para alguns passos de MC, ver Figura 3.

Figure 3. Instantâneos da membrana lipídica em fase fluida como (A) configuração inicial, (B) depois de aumentar o tamanho do bico em direcção y por um factor de (1 + η), e (C) o bico relaxado fixando o tamanho da membrana em direcção y e variável em direcção x. Como consequência do rácio positivo de Poisson para o bico nesta fase, o tamanho da membrana no sentido x é reduzido e equilibrado após alguns passos de MC. As contas da cabeça e da cauda do bico são mostradas em vermelho e verde, respectivamente.
p>Durante a simulação, para acelerar o procedimento de termização depois de estender a caixa na direcção axial, aumentamos ligeiramente a temperatura no sistema, o que resulta na produção de mais mobilidade para as partículas. Para a fase do fluido, definimos a temperatura inicial para T = 1,3 e depois alterámo-la para T = 1,4 para cerca de 400 passos extra e depois alterámos de volta para o valor original. Da mesma forma, para as fases gel e interdigitadas, as temperaturas iniciais foram T = 1,08 e T = 1,16 e foram trocadas para T = 1,2 e T = 1,3, respectivamente.
Uma análise comum das propriedades elásticas de uma membrana baseia-se no Helfrich Hamiltonian (Helfrich, 1973), que descreve o custo da entalpia elástica livre associada a flutuações da altura da membrana (desvios da superfície plana). Ao parametrizar a membrana em coordenadas cartesianas (x,y) →(x,y,h(x,y)) (Monge gauge), o Helfrich Hamiltonian é, para pequenas flutuações, dado por
onde kc é a rigidez à flexão e σ é a tensão superficial. A equação (4) é aplicada quando a membrana é considerada como um corpo com espessura zero. Uma teoria elástica generalizada para membranas com espessuras finitas foi sugerida por Brannigan e Brown (2006) e aplicada ao modelo Lenz-Schmid recentemente (West et al., 2009; Neder et al.., 2010).
Para determinar h(x, y) a partir das simulações, discretizámos o (x, y)-plano numa grelha regular com espaçamento 2σLJ, determinada em cada célula (i, j) a média das coordenadas z+(i, j) e z-(i, j) das contas de cabeça no folheto superior e inferior, respectivamente, e calculámos a altura h(i, j) – /2 (a média h¯ foi subtraída posteriormente). Para uma membrana de tamanho lateral L × L, Eq. (4) prevê:
para o espectro de potência das flutuações, onde ĥ(q) é a transformada de Fourier de h(x, y) no vector de onda q, q = |q|, e <> denota uma média de equilíbrio. Nos numéricos, ĥ(q) é calculado a partir de uma transformação de Fourier discreta de h(i, j). É evidente que Eq. (5) só se pode manter verdadeiro para uma gama q 2π/L ≪ q ≪ ≪/σLJ, onde nem o tamanho finito do sistema nem o tamanho (atomístico) do grânulo afectam as flutuações. O intervalo q correspondente para os tamanhos do sistema, que pode ser utilizado dentro de um tempo de computação razoável, infelizmente não é grande, mas cabe de < |ĥ(q)|2 > ∕kBTL2 em função de q2 num intervalo 0.5 ≤ q2 ≤ 1 produz um bom acordo com Eq. (5) para os nossos tamanhos.
Resultados e Discussões
Na Tabela 3, os rácios de Poisson obtidos νyx, νzx, e νxy assim como νzy para diferentes fases são resumidos. Como demonstrado na Figura 4, a razão de Poisson obtida desta forma é independente do factor de redimensionamento η desde que η não seja demasiado grande, o que leva a destruir a estrutura da membrana nem demasiado pequena, cuja dose não produz espaço livre suficiente para as partículas se moverem. De acordo com o Quadro 3 e a Figura 4, as fases fluida e interdigitada têm a mesma razão de Poisson medida para ambas as direcções x e y. Isto significa que estas duas fases são isotrópicas no plano do bileiro. No entanto, este já não é o caso para a fase de gel. As medições mostram que, um bico na fase de gel comporta-se como um material anisotrópico, que tem dois valores distintos para as duas direcções diferentes no plano do bico.

Tabela 3. Constantes elásticas obtidas a partir de simulações de membranas lipídicas em diferentes fases.

Figura 4. Relaxamento de -ΔLi/ηjLi em (A) fluido, (B) interdigitado, e (C) fase de gel. O valor de platô alcançado após cerca de 5000 passos MC, independentemente do valor de η, produz a razão de Poisson ν. Na fase de gel, a razão de Poisson tem valores diferentes para νxy e νyx e esta fase actua como uma superfície anisotrópica.
Conversamente, quando o bico foi estendido na direcção perpendicular ao plano de inclinação, os lípidos reorganizam-se de tal forma que o bico encolhe lateralmente. Para o presente trabalho, os comprimentos de ligação dos lípidos no sentido z (perpendicular ao plano do bico) não foram redimensionados. A razão é que, para observar o efeito de Poisson, o comprimento entre as contas deve ser redimensionado por um factor, que produz espaço suficiente para as partículas se redimensionarem. No entanto, no sentido z, este aumento deve ocorrer entre as contas coladas dentro de um lipídio, o que provoca uma quebra da ligação. Os valores reportados para νzx e νzy são as alterações do comprimento relativo no comprimento médio do bico devido à extensão lateral dos bicos no sentido x e y, respectivamente.
Os valores obtidos para a rigidez de flexão kc são 5.2ϵ para a fase fluida, e 7.6ϵ para a fase interdigitada. Para as fases de gel e fluido, os resultados concordam com os relatórios computacionais anteriores (West, 2008; West et al., 2009) e resultados experimentais (Falcioni et al., 1997; Liu e Zhang, 2009). A densidade espectral para a fase interdigitada foi calculada de acordo com o mesmo método. Relatamos aqui a rigidez de flexão para a fase interdigitada. A figura 5 ilustra os espectros de flutuação da altura para três fases estudadas e encaixa na Eq. (5).
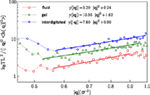
Figure 5. Espectros de flutuação para o fluido, gel, e fases interdigitadas e encaixa na Eq. (5).
Com a teoria da elasticidade bidimensional, a rigidez de flexão kc está relacionada com a razão de Poisson ν e o módulo E de Young de acordo com (Landau et al.., 1986)
onde d é a espessura média da membrana, para a qual obtemos, 5.48σLJ, e 4.86σLJ para o fluido, e fases interdigitadas, respectivamente. Substituindo os valores fundados para os rácios de Poisson e a rigidez de flexão para biletes em duas fases isotrópicas por Eq. (6), pode-se obter o moduli de acordo com Young. Os modulos de Young calculados desta forma são 0,28 e 0,67 em unidades de ϵ/σ3 para os estados fluido e interdigitado, respectivamente. Obviamente, a anisotropicidade observada na dose da fase de gel não permite utilizar o teorema acima para o bílis nesta fase.
A abordagem apresentada neste artigo poderia ser aplicada a membranas com composições lipídicas mais complexas, dado que os modelos de interacção verificados experimentalmente existem para esses lípidos. A abordagem também poderia ser combinada com uma simulação mais precisa dos bílis. Simulações atomísticas completas e em particular simulações ab initio, poderiam, em princípio, fornecer descrições mais precisas do sistema, mas vêm com uma enorme carga computacional (Mashaghi et al., 2012, 2013a).
Conclusion
Fizemos simulações Monte Carlo do modelo de bílis lipídicos de granulação grosseira para obter uma visão das propriedades mecânicas das membranas lipídicas planas. Utilizando um método de redimensionamento, pudemos determinar a razão de Poisson ν para diferentes fases, além da rigidez de flexão determinada a partir de uma análise das flutuações da altura da membrana baseada no Helfrich Hamiltonian. Isto permite-nos calcular também o módulo E do Young para diferentes fases. A abordagem é precisa, fácil de implementar e pode ser aplicada a outras membranas como o grafeno (Abedpour et al., 2010), a fim de prever a dependência da temperatura do seu rácio de Poisson e do módulo de Young. Outros sistemas interessantes a estudar são os nanofios metálicos cristalinos onde o módulo elástico controla o seu desempenho estrutural e comportamento funcional, como a sua frequência de ressonância sob carga oscilatória tipicamente aplicada durante o accionamento e a detecção (Chen et al., 2006; McDowell et al.., 2008).
Conflict of Interest Statement
Os autores declaram que a pesquisa foi realizada na ausência de quaisquer relações comerciais ou financeiras que pudessem ser interpretadas como um potencial conflito de interesses.
Abrigações
Gostaríamos de agradecer a Philipp Maass pelas suas úteis discussões.
Abedpour, N.., Asgari, R., e Tabar, M. R. R. (2010). Irreversibilidade em resposta a forças que actuam em folhas de grafeno. Phys. Rev. Lett. 104, 196804. doi:10.1103/PhysRevLett.104.196804
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Ayton, G., Smondyrev, A., Bardenhagen, S., McMurtry, P., e Voth, G. (2002). Cálculo do módulo de massa para um bocal lipídico com simulação de dinâmica molecular semquilibrio. Biofísica. J. 82, 1226-1238. doi:10.1016/S0006-3495(02)75479-9
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Brannigan, G., e Brown, F. L. H. (2006). Um modelo consistente para flutuações térmicas e deformações induzidas por proteínas em bílis lipídicos. Biofísicos. J. 90, 1501. doi:10.1529/biophysj.105.075838
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chen, C., Shi, Y., Zhang, Y., Zhu, J., e Yan, Y. (2006). Dependência de tamanho do módulo de Young em nanowires ZnO. Phys. Rev. Lett. 96, 075505. doi:10.1103/PhysRevLett.96.075505
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chernomordik, L. V., e Kozlov, M. M. (2008). Mecânica da fusão por membranas. Nat. Estrutura. Mol. Biol. 15, 675-683. doi:10.1038/nsmb.1455
CrossRef Full Text
Claesson, M., Frost, R., Svedhem, S., e Andersson, M. (2011). Bilhares lipídicos de poros em sílica mesoporosa com poros de tamanho variável. Langmuir 27, 8974-8982. doi:10.1021/la201411b
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Falcioni, M., Bowick, M. J., Guitter, E., e Thorleifsson, G. (1997). A razão Poisson das superfícies cristalinas. Europhys. Lett. 38, 67-72. doi:10.1016/j.jhazmat.2010.12.101
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Goetz, R., e Lipowsky, R. (1998). Simulações computorizadas de membranas de bilayer: auto-montagem e tensão interfacial. J. Chem. Phys. 108, 7397-7409. doi:10.1063/1.476160
CrossRef Full Text
Grest, G. S., e Kremer, K. (1986). Simulação da dinâmica molecular para polímeros na presença de um banho de calor. Phys. Rev. A 33, 3628-3631. doi:10.1103/PhysRevA.33.3628
CrossRef Full Text
Hall, L., Coluci, V., Galvao, D., Kozlov, M., Zhang, M., Dantas, S., et al. (2008). Mudança de sinal da razão de Poisson para folhas de nanotubo de carbono. Science 320, 504-507. doi:10.1126/science.1149815
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Helfrich, W. (1973). Propriedades elásticas dos bílis lipídicos – teoria e possíveis experiências. Z. Naturforsch. C 28, 693.
Illya, G., Lipowsky, R., e Shillcock, J. C. (2005). Efeito do comprimento e assimetria da cadeia nas propriedades materiais das membranas do bico. J. Chem. Phys. 122, 1-6. doi:10.1063/1.1917794
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Jeon, J., e Voth, G. (2005). As respostas dinâmicas de tensão à mudança de área nas membranas de bílis lipídico planar. Biofísicos. J. 88, 1104-1119. doi:10.1529/biophysj.104.052183
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Landau, L. D., Pitaevskii, L. P., Lifshitz, E. M., e Kosevich, A. M. (1986). Theory of Elasticity, Volume 7, 3ª Edn. Oxford: Butterworth-Heinemann.
Lenz, O. (2007). Simulação Computadorizada de Bilhares Lipídicos. Tese de doutoramento, Universidade de Bielefeld, Bielefeld.
Lenz, O., e Schmid, F. (2005). Um modelo simples de computador para bilayers líquidos lipídicos. J. Mol. Liq. 117, 147-152. doi:10.1016/j.molliq.2004.08.008
CrossRef Full Text
Lindahl, E., e Edholm, O. (2001). Simulação da dinâmica molecular das taxas de relaxamento NMR e da dinâmica lenta em bílis lipídicos. J. Chem. Phys. 115, 4938-4950. doi:10.1529/biophysj.107.121806
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Liu, P., e Zhang, Y. W. (2009). Rigidez de flexão do grafeno dependente da temperatura. Aplic. Phys. Lett. 94, 231912. doi:10.1063/1.3155197
CrossRef Full Text
Martins, B., e Galvao, D. (2010). Nanoribões de grafeno curvos: estrutura e dinâmica dos nanobeltros de carbono. Nanotecnologia 21, 075710. doi:10.1088/0957-4484/21/7/075710
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Martins, P., Malhaire, C., Brida, S., e Barbier, D. (2009). Sobre a determinação da proporção de Poisson de filmes de monolayer e bilayer submicron grossos em tensão. Microssista. Technol. 15, 1343-1348. doi:10.1007/s00542-009-0822-5
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mashaghi, A.., Partovi-Azar, P., Jadidi, T., Nafari, N., Esfarjani, K., Maass, P., et al. (2012). A água interfacial facilita a transferência de energia ao induzir vibrações alargadas nos lípidos de membrana. J. Phys. Chem. B 116, 6455-6460. doi:10.1021/jp302478a
CrossRef Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Anvari, M., Panahian, J. S., Nafari, N., et al. (2013a). Autoionização melhorada da água em interfaces fosfolípidos. J. Phys. Chem. C 117, 510-514. doi:10.1021/jp3119617
CrossRef Full Text
Mashaghi, S., Jadidi, T., Koenderink, G., e Mashaghi, A. (2013b). Nanotecnologia lipídica. Int. J. Mol. Sci. 14, 4242-4282. doi:10.3390/ijms14024242
CrossRef Full Text
McDowell, M., Leach, A., e Gall, K. (2008). Sobre o módulo elástico dos nanofios metálicos. Nano Lett. 8, 3613-3618. doi:10.1021/nl801526c
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mitchell, J. S., Zorman, C. A., Kicher, T., Roy, S., e Mehregany, M. (2003). Exame do teste de protuberância para determinar o stress residual, módulo de Young, e rácio de Poisson de filmes finos 3c-sic. J. Aerosp. Eng. 16, 46-54. doi:10.1061/(ASCE)0893-1321(2003)16:2(46)
CrossRef Full Text
Morone, N., Fujiwara, T., Murase, K., Kasai, R. S., Ike, H., Yuasa, S., et al. (2006). Reconstrução tridimensional do esqueleto de membrana na interface de membrana plasmática por tomografia electrónica. J. Cell Biol. 174, 851-862. doi:10.1083/jcb.200606007
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Nagle, J. F., e Tristram-Nagle, S. (2000). Estrutura dos bílis lipídicos. Biochim. Biófilos. Acta 1469, 159-195. doi:10.1016/S0304-4157(00)00016-2
CrossRef Full Text
Neder, J., West, B., Nielaba, P., e Schmid, F. (2010). Simulações de membranas sob tensão com granulação grosseira. J. Chem. Phys. 132, 115101. doi:10.1063/1.3352583
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Popescu, G.., Ikeda, T., Goda, K., Best-Popescu, C. A., Laposata, M., Manley, S., et al. (2006). Medição óptica da tensão da membrana celular. Phys. Rev. Lett. 97, 218101. doi:10.1103/PhysRevLett.97.218101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Sansom, D. M. S. P., e Biggin, P. C. (2010). Simulações Moleculares e Biomembranas: Da Biofísica à Função, 1ª Edn. Cambridge, UK: Royal Society of Chemistry.
Schmidt, D., e MacKinnon, R. (2008). O canal k+ dependente da tensão e a sensibilidade à toxina do sensor de tensão dependem do estado mecânico da membrana lipídica. Proc. Natl. Acad. Sci. U.S.A. 105, 19276-19281. doi:10.1073/pnas.0810187105
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Seto, H., Yamada, N., Nagao, M., Hishida, M., e Takeda, T. (2008). Módulo de flexão de balizas lipídicas numa fase líquido-cristalina incluindo um regime de inchaço anómalo estimado por experiências de eco de neutrões spin. Eur. Phys. J. E Soft Matter 26, 217-223. doi:10.1140/epje/i2007-10315-0
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Thakkar, F. M., Maiti, P., Kumarana, V., e Ayappa, K. (2011). Verificação de escalas para a rigidez de flexão de membranas de bílis usando modelos de mesoscala. Soft Matter 7, 3963-3966. doi:10.1039/c0sm00876a
CrossRef Full Text
Tierney, K. J., Block, D. E., e Longo, M. L. (2005). Elasticidade e comportamento de fase da membrana DPPC modulada por colesterol, ergosterol e etanol. Biofísica. J. 89, 2481-2493. doi:10.1529/biophysj.104.057943
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
West, B. (2008). Interacções Lípido-Proteína em Membranas Lipídicas. Tese de doutoramento, Universidade de Bielefeld, Bielefeld.
West, B., Brown, F. L. H., e Schmid, F. (2009). Interacções membrane-proteína num modelo genérico de granulado grosseiro para bílis lipídicos. Biofísicos. J. 96, 101. doi:10.1529/biophysj.108.138677
P>Pubmed Abstract | Pubmed Full Text | CrossRef Full Text