Having definiu que, a função logarítmica y = log b x é a função inversa da função exponencial y = b x. Podemos agora proceder à representação gráfica das funções logarítmicas olhando para a relação entre as funções exponenciais e logarítmicas.
Mas antes de saltar para o tópico de funções logarítmicas gráficas, é importante que nos familiarizemos com os seguintes termos:
- li> O domínio de uma função
O domínio de uma função é um conjunto de valores que pode substituir na função para obter uma resposta aceitável.
- O domínio de uma função
Este é o conjunto de valores que obtém após substituir os valores no domínio pela variável.
- li>Asymptotes
Existem três tipos de assímptotes, nomeadamente; vertical, horizontal, e oblíqua. A assímptota vertical é o valor de x onde a função cresce sem limite nas proximidades.
Assímptotas horizontais são valores constantes que f(x) se aproximam à medida que x cresce sem limite. As assímptotas oblíquas são polinómios de primeiro grau que f(x) se aproxima à medida que x cresce sem limite.
Como fazer o gráfico das funções logarítmicas?
Grafar uma função logarítmica pode ser feito examinando o gráfico exponencial da função e depois trocando x e y.
O gráfico de uma função exponencial f (x) = b x ou y = b x contém as seguintes características:
- O domínio de uma função exponencial é números reais (-infinidade, infinidade).
- O intervalo é também números reais positivos (0, infinidade)
- O gráfico de uma função exponencial passa normalmente através do ponto (0, 1). Isto significa que a intercepção y – intercepção está no ponto (0, 1).
- O gráfico de uma função exponencial f(x) = b x tem uma assímptota horizontal a y = 0.
- Um gráfico exponencial diminui da esquerda para a direita se 0 < b < 1, e este caso é conhecido como decadência exponencial.
- Se a base da função f(x) = b x for superior a 1, então o seu gráfico aumentará da esquerda para a direita e é chamado crescimento exponencial.
Ao observarmos as características acima, uma de cada vez, podemos igualmente deduzir as características das funções logarítmicas como se segue:
- Uma função logarítmica terá o domínio como (0, infinito).
- O alcance de uma função logarítmica é (-infinidade, infinito).
- O gráfico da função logarítmica passa pelo ponto (1, 0), que é o inverso de (0, 1) para uma função exponencial.
- O gráfico de uma função logarítmica tem uma assíntota vertical em x = 0,
- O gráfico de uma função logarítmica diminuirá da esquerda para a direita se 0 < b < 1.
- E se a base da função for maior que 1, b > 1, então o gráfico aumentará da esquerda para a direita.
Como fazer o gráfico de uma função logarítmica básica?
Uma função logarítmica básica é geralmente uma função sem deslocamento horizontal ou vertical.
Aqui estão os passos para criar um gráfico de uma função logarítmica básica.
- Desde que todas as funções logarítmicas passem através do ponto (1, 0), localizamos e colocamos um ponto no ponto.
- Para evitar que a curva toque no eixo y, desenhamos uma assímptota a x = 0,
- Se a base da função for superior a 1, aumente a sua curva da esquerda para a direita. Da mesma forma, se a base for inferior a 1, diminua a curva da esquerda para a direita.
Agora vejamos os seguintes exemplos:
Exemplo 1
Graph a função logarítmica f(x) = log 2 x e o alcance e domínio do estado da função.
Solução
- Obviamente, uma função logarítmica deve ter o domínio e o intervalo de (0, infinito) e (-infinidade, infinito)
- Desde que a função f(x) = log 2 x seja superior a 1, aumentaremos a nossa curva da esquerda para a direita, um mostrado abaixo.
- Não podemos ver a assímptota vertical em x = 0 porque está escondida pelo eixo y.
Exemplo 2
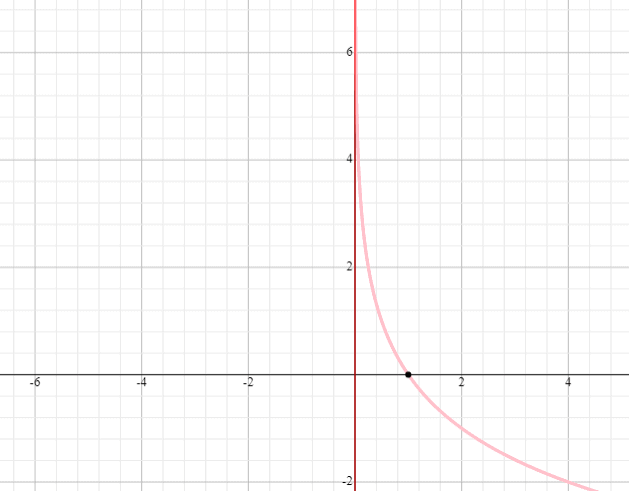
Desenhar um gráfico de y = log 0,5 x
Solução
- Colocar um ponto no ponto (1, 0). Todas as curvas logarítmicas passam por este ponto.
- Desenhar uma assímptota em x = 0,
- Li>Desde que a base da função y = log 5 x seja inferior a 1, diminuiremos a nossa curva da esquerda para a direita.
- A função y = log 5 x terá também (0, infinito) e (-infinidade, infinito) como domínio e alcance.
Grafar uma função logarítmica com um deslocamento horizontal
Funções logarítmicas com um deslocamento horizontal são da forma f(x) = log b (x + h) ou f (x) = log b (x – h), onde h = o deslocamento horizontal. O sinal do deslocamento horizontal determina a direcção do deslocamento. Se o sinal for positivo, o deslocamento será negativo, e se o sinal for negativo, o deslocamento tornar-se-á positivo.
Ao aplicar o deslocamento horizontal, as características de uma função logarítmica são afectadas das seguintes formas:
- A intercepção x – move para a esquerda ou para a direita uma distância fixa igual a h.
- A assimetria vertical move uma distância igual a h.
- O domínio da função também muda.
Exemplo 3
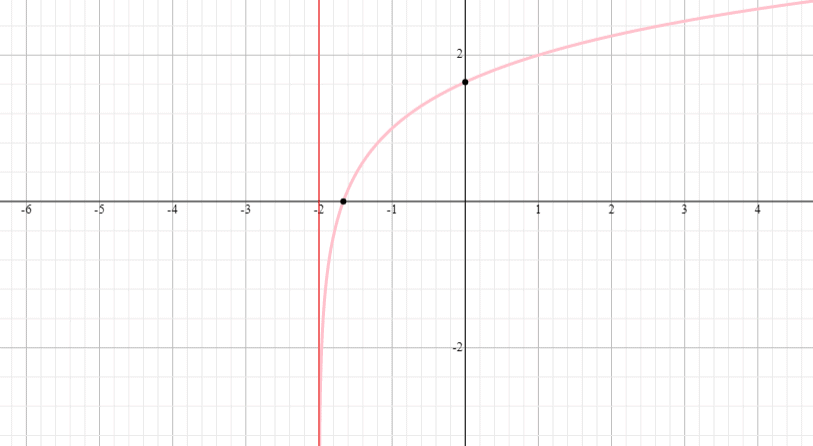
Desenhar um gráfico da função f(x) = log 2 (x + 1) e indicar o domínio e o alcance da função.
Solução
⟹ Domínio: (- 1, infinito)
⟹ Gama: (-infinidade, infinito)
Exemplo 4
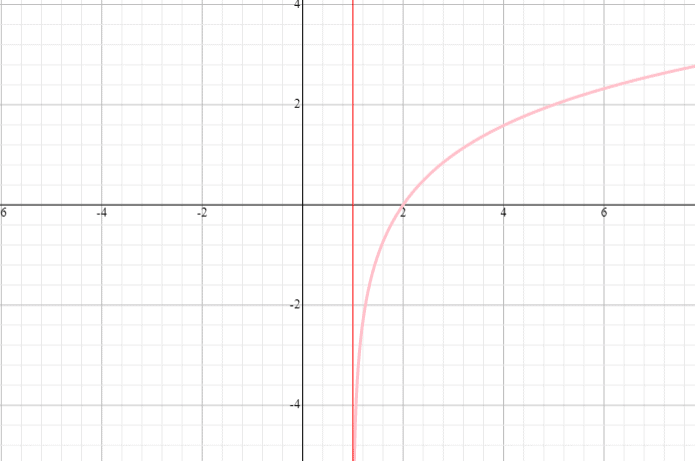
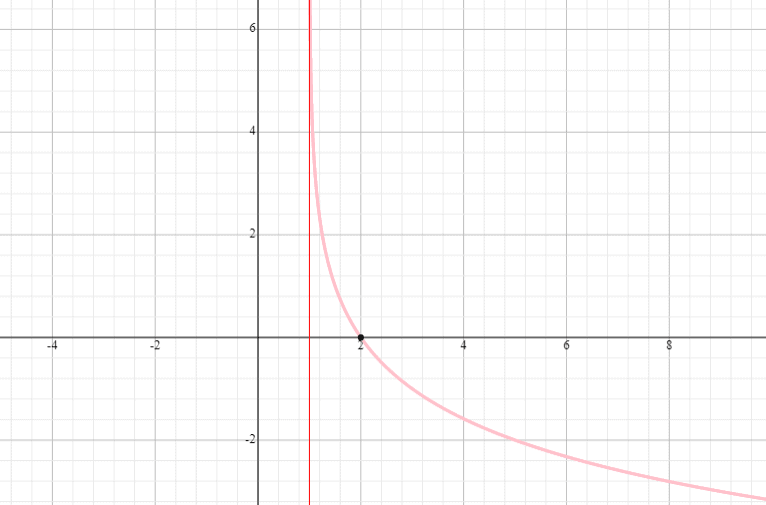
Gráfico y = log 0,5 (x – 1) e indicar o domínio e o intervalo.
Solução
⟹ Domínio: (1, infinidade)
⟹ Gama: (-infinidade, infinidade)
Como fazer o gráfico de uma função com um deslocamento vertical?
Uma função logarítmica com deslocamento horizontal e vertical é da forma f(x) = log b (x) + k, onde k = o deslocamento vertical.
O deslocamento vertical afecta as características de uma função da seguinte forma:
- O intercepção x deslocar-se-á para cima ou para baixo com uma distância fixa de k
Exemplo 5
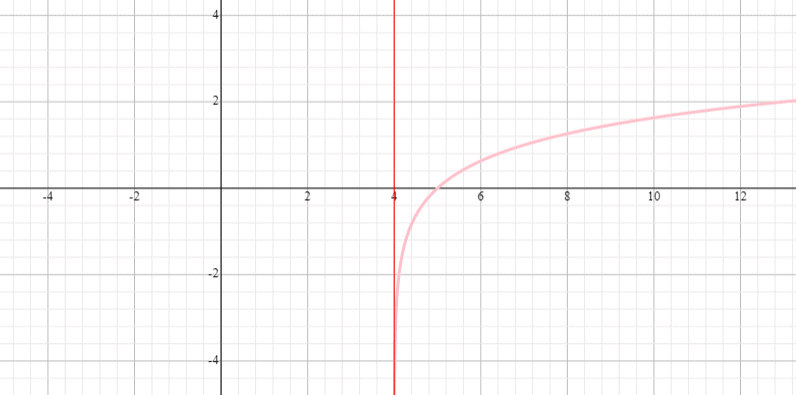
Gráfico da função y = log 3 (x – 4) e indicar o alcance e domínio da função.
Solução
⟹ Domínio: (0, infinito)
⟹ Intervalo: (-infinidade, infinidade)
Funções com deslocamento horizontal e vertical
Uma função logarítmica com deslocamento horizontal e vertical é da forma (x) = log b (x + h) + k, onde k e h são os deslocamentos vertical e horizontal, respectivamente.
Exemplo 6
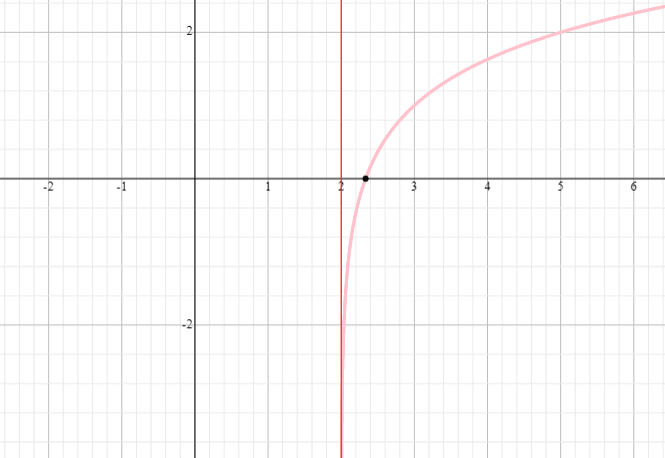
Gráfico da função logarítmica y = log 3 (x – 2) + 1 e encontrar o domínio e alcance da função.
Solução
⟹ Domínio: (2,infinito)
⟹ Gama: (-infinidade, infinidade)
Exemplo 7
Gráfico da função logarítmica y = log 3 (x + 2) + 1 e encontrar o domínio e o intervalo da função.
Solução
⟹ Domínio: (- 2,infinito)
⟹ Gama: (-infinidade, infinidade)