Regressão Probit
Na regressão Probit, a função cumulativa de distribuição normal normal é utilizada para modelar a função de regressão quando a variável dependente é binária, ou seja, assumimos que a variável dependente é binária
(\beta_0 + \beta_1 X) em (11.4) desempenha o papel de um quantil. Lembre-se de que o coeficiente Probit em (11,4) é a mudança em (z) associada a uma mudança de uma unidade em (X). Embora o efeito sobre z de uma alteração em X seja linear, a ligação entre z e a variável dependente Y é não linear, uma vez que X é uma função não linear de X.
p>Desde que a variável dependente é uma função não linear dos regressores, o coeficiente em X não tem uma interpretação simples. De acordo com o Key Concept 8.1, a mudança esperada na probabilidade de que \(Y=1) devido a uma mudança na relação P/I pode ser calculada da seguinte forma:
- Compute a probabilidade prevista de que \(Y=1) para o valor original de \(X=).
- Calcule a probabilidade prevista que \(Y=1\) para \(X + \Delta X\).
- Calcule a diferença entre ambas as probabilidades previstas.
Obviamente, podemos generalizar (11,4) a regressão Probit com múltiplos regressores para mitigar o risco de enfrentar o viés de variáveis omitidas. Os fundamentos da regressão de Probit estão resumidos no Key Concept 11.2.
Probit Model, Predicted Probabilities and Estimated Effects
Assumir que \(Y\) é uma variável binária. O modelo
com o modelo Probit da população com múltiplos regressores { X_1, X_2, {dots, X_k} e {Phi(cdot)} é a função de distribuição normal cumulativa.
A probabilidade prevista de que {(Y=1}) dado {X_1, X_2, {pontos, X_k}) possa ser calculado em duas etapas:
-
Compute \(z = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_k X_k)
-
p>Localize \(\Phi(z)}) chamando pnorm().
(b) é o efeito sobre { z} de uma mudança de uma unidade no regressor { X_j}, mantendo constantes todos os outros regressores.
O efeito sobre a probabilidade prevista de uma mudança num regressor pode ser calculado como no Conceito chave 8.1.
Em R, os modelos Probit podem ser estimados usando a função glm() das estatísticas do pacote. Usando a família de argumentos especificamos que queremos usar uma função de ligação Probit.
Estimamos agora um modelo Probit simples da probabilidade de uma negação de hipoteca.
# estimate the simple probit modeldenyprobit <- glm(deny ~ pirat, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1O modelo estimado é
\
p>P>Apenas como no modelo de probabilidade linear verificamos que a relação entre a probabilidade de negação e o rácio pagamentos/receitas é positiva e que o coeficiente correspondente é altamente significativo.
O seguinte trecho de código reproduz a figura 11.2 do livro.
# plot dataplot(x = HMDA$pirat, y = HMDA$deny, main = "Probit Model of the Probability of Denial, Given P/I Ratio", xlab = "P/I ratio", ylab = "Deny", pch = 20, ylim = c(-0.4, 1.4), cex.main = 0.85)# add horizontal dashed lines and textabline(h = 1, lty = 2, col = "darkred")abline(h = 0, lty = 2, col = "darkred")text(2.5, 0.9, cex = 0.8, "Mortgage denied")text(2.5, -0.1, cex= 0.8, "Mortgage approved")# add estimated regression linex <- seq(0, 3, 0.01)y <- predict(denyprobit, list(pirat = x), type = "response")lines(x, y, lwd = 1.5, col = "steelblue")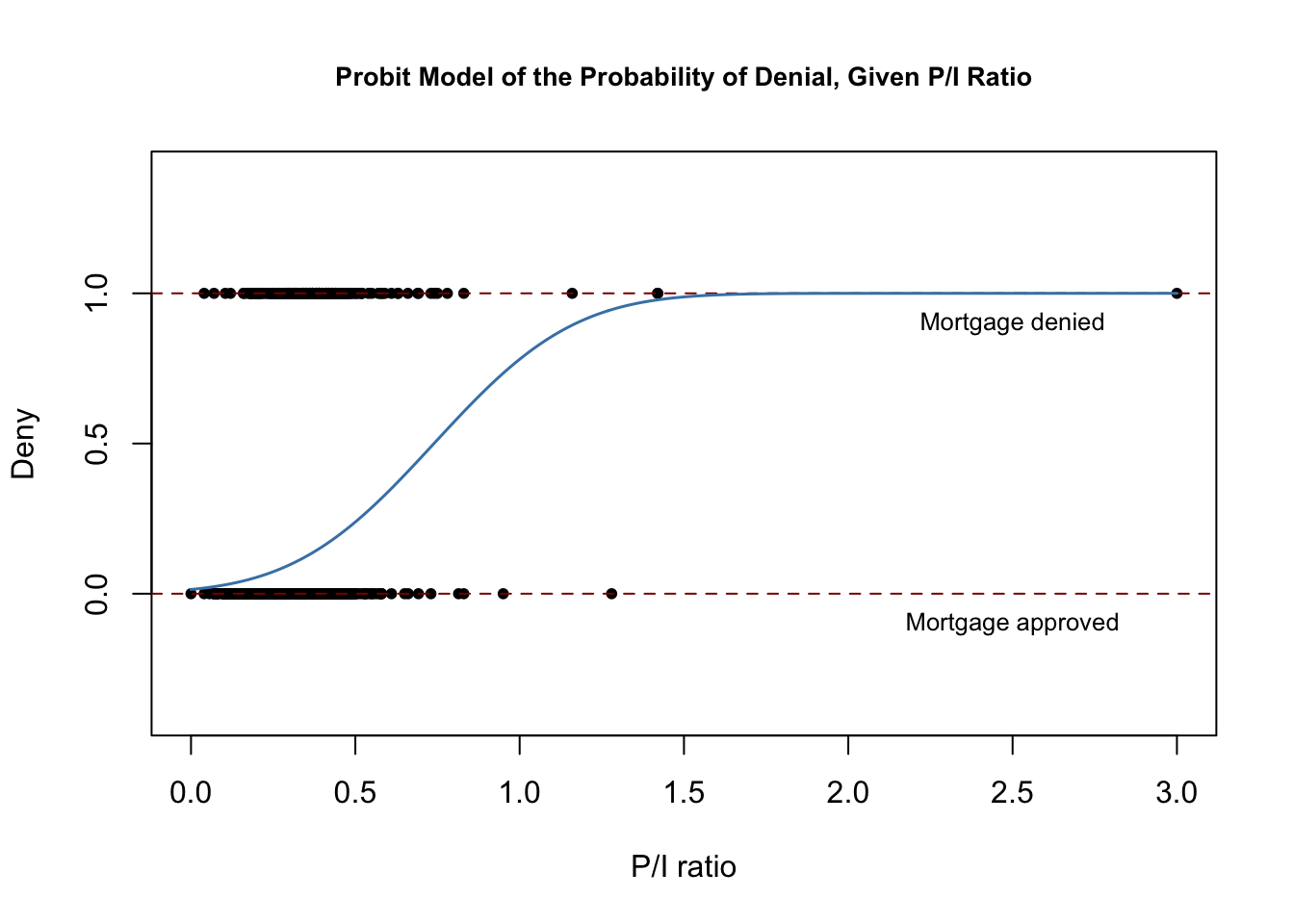
A função de regressão estimada tem uma forma “S”-shape esticada que é típica para o CDF de uma variável aleatória contínua com PDF simétrico como o de uma variável aleatória normal. A função é claramente não linear e achatada para valores grandes e pequenos de relação P/I. A forma funcional assegura assim também que as probabilidades condicionais previstas de uma negação se situam entre \(0\) e \(1\).
Usamos a previsão() para calcular a mudança prevista na probabilidade de negação quando a relação P/I é aumentada de \(0).3\) para \(0,4\).
# 1. compute predictions for P/I ratio = 0.3, 0.4predictions <- predict(denyprobit, newdata = data.frame("pirat" = c(0.3, 0.4)), type = "response")# 2. Compute difference in probabilitiesdiff(predictions)#> 2 #> 0.06081433Verificamos que um aumento no rácio pagamento/receitas de 0,3\) para 0,4\) é previsto para aumentar a probabilidade de negação em aproximadamente 6.2\%).
Continuamos a utilizar um modelo Probit aumentado para estimar o efeito da raça na probabilidade de negação de um pedido de hipoteca.
denyprobit2 <- glm(deny ~ pirat + black, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1A equação do modelo estimado é
>p>>/p>
Enquanto todos os coeficientes são altamente significativos, tanto os coeficientes estimados sobre o rácio pagamentos/rendimentos como o indicador para a descendência afro-americana são positivos. Mais uma vez, os coeficientes são difíceis de interpretar mas indicam que, em primeiro lugar, os afro-americanos têm uma maior probabilidade de negação do que os candidatos brancos, mantendo constante o rácio pagamentos/rendimentos e, em segundo lugar, os candidatos com um elevado rácio pagamentos/rendimentos enfrentam um risco mais elevado de serem rejeitados.
Quanta diferença estimada nas probabilidades de negação entre dois candidatos hipotéticos com o mesmo rácio pagamentos/rendimentos? Como anteriormente, podemos utilizar a previsão() para calcular esta diferença.
# 1. compute predictions for P/I ratio = 0.3predictions <- predict(denyprobit2, newdata = data.frame("black" = c("no", "yes"), "pirat" = c(0.3, 0.3)), type = "response")# 2. compute difference in probabilitiesdiff(predictions)#> 2 #> 0.1578117Neste caso, a diferença estimada nas probabilidades de recusa é de cerca de \(15,8\%).