

Outliers Formula (Table of Contents)
- li>Outli>Outli FormulaExemplos de Fórmula de Outliers (With Excel Template)
Outliers Formula
In statistics, Os outliers são os dois pontos excepcionalmente distantes extremos nos conjuntos de dados em questão. Os valores extremamente altos e os valores extremamente baixos são os valores aberrantes de um conjunto de dados. Isto é muito útil para encontrar qualquer falha ou erro que tenha ocorrido. Simplesmente como o nome diz, os valores aberrantes são os valores aberrantes dos restantes valores do conjunto de dados. Exemplo, considere os estudantes de engenharia e imagine que eles tinham anões na sua turma. Assim, os anões são as pessoas que têm uma altura extremamente baixa quando comparadas com outras pessoas de altura normal. Portanto, este é o valor mais alto desta turma. Os valores mais antigos podem ser calculados utilizando o método Tukey.
Inicie o seu Curso Bancário de Investimento Gratuito
Download Corporate Valuation, Banca de Investimento, Contabilidade, Calculadora CFA & outros
Fórmula para Outliers –
Higher Outlier= Q3 + (1,5 * IQR)
Exemplos de Fórmula de Outliers (Com o Modelo Excel)
Vamos dar um exemplo para compreender melhor o cálculo da fórmula para Outliers.
Outliers Formula – Exemplo #1
Consulte o seguinte conjunto de dados e calcule os outliers para o conjunto de dados.
Conjunto de dados = 5, 2, 7, 98, 309, 45, 34, 6, 56, 89, 23
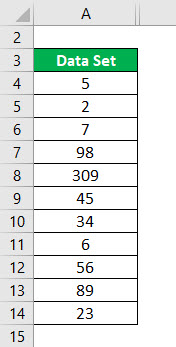

Ordem ascendente do conjunto de dados:
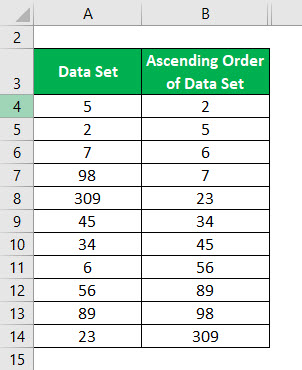

Mediana do conjunto de dados da ordem ascendente é calculada como:
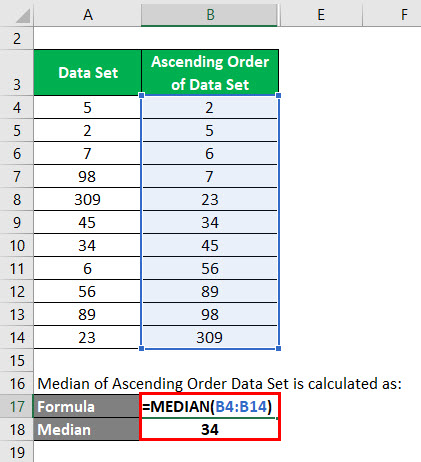

Neste conjunto de dados, o número total de dados é 11. Portanto, n= 11. Mediana = 11+1/2 = 12 / 2 = 6. Assim, o valor que está na 6ª posição neste conjunto de dados é a mediana.
Então valor da mediana = 34.
Dividir o conjunto de dados em 2 metades usando a mediana.
4.9 (3,296 classificações)
Ver Curso
Curso para Gestores Não Financeiros (7 Cursos)
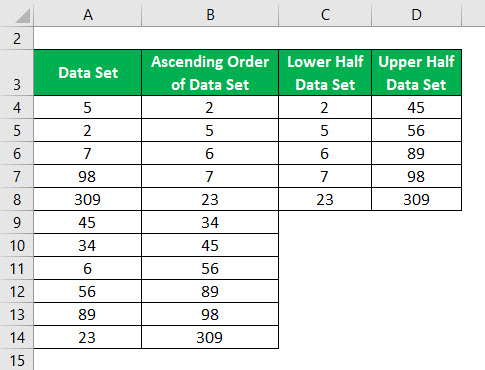

Median of Lower Half and Upper Half Data Set is calculated as:
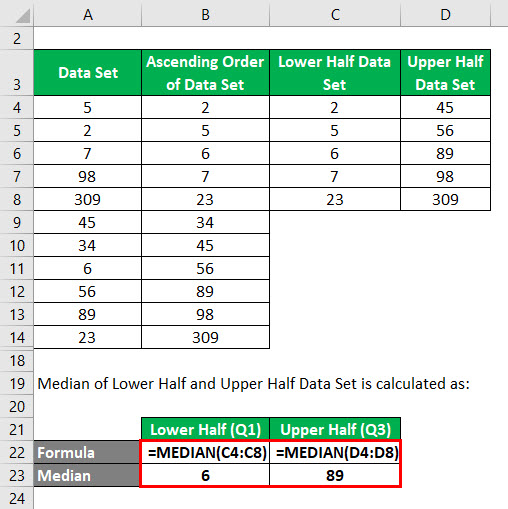

- Na metade inferior 2, 5, 6,7,23, se encontrarmos a mediana como encontramos no passo 2, o valor da mediana seria 6. Assim Q1= 6,
- Na metade superior 45, 56, 89, 98,309, se encontrarmos a mediana como encontrámos no passo 2, o valor da mediana seria 89. Assim, Q3= 89.
IQR é calculado utilizando a fórmula dada abaixo
IQR = Q3 – Q1
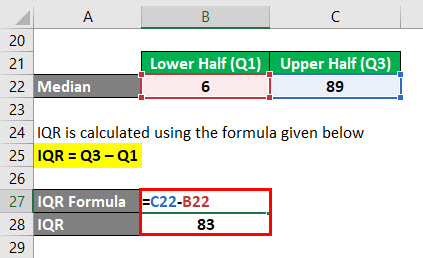

- IQR = 89 -6
- IQR = 83
Lower Outlier é calculado usando a fórmula dada abaixo
Lower Outlier = Q1 – (1.5 * IQR)
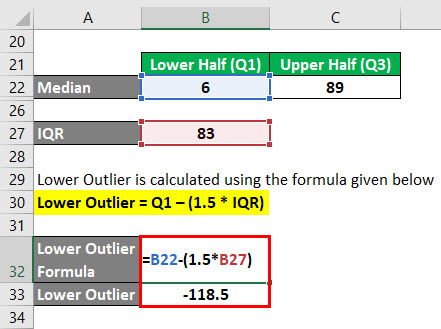

- Outli>Outlier Mais Baixo = 6 – (1.5 * 83)
- Lower Outlier = -118.5
Higher Outlier é calculado usando a fórmula dada abaixo
Higher Outlier = Q3 + (1.5 * IQR)
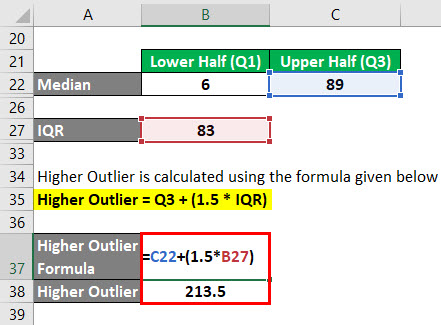

- Higher Outlier = 89 + (1.5 * 83)
- Higher Outlier = 213,5
Agora, buscar estes valores no conjunto de dados -118,5, 2, 5, 6, 7, 23, 34, 45, 56, 89, 98, 213,5, 309. Os valores que estão abaixo no valor do lado inferior e acima no valor do lado superior são o valor mais baixo. Para este conjunto de dados, 309 é o outlier.
Outliers Formula – Exemplo #2
Considerar o seguinte conjunto de dados e calcular os outliers para o conjunto de dados.
Dados = 45, 21, 34, 90, 109.

Ordem decrescente do conjunto de dados:
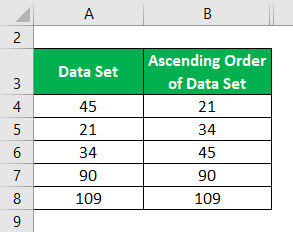

Mediana do Conjunto de Dados de Ordem Ascendente é calculada como:
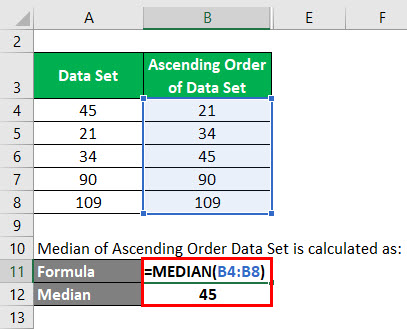

Neste conjunto de dados, o número total de dados é 5. Então n = 5. Mediana = 5+1/2 = 6 / 2 = 3. Assim, o valor que está na 3ª posição neste conjunto de dados é a mediana.
Então o valor da mediana = 45.
Dividir o conjunto de dados em 2 metades usando a mediana.
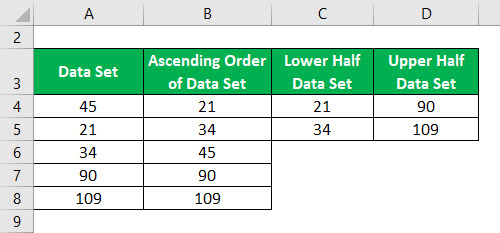

Mediana do Conjunto de Dados da Metade Inferior e da Metade Superior é calculada como:
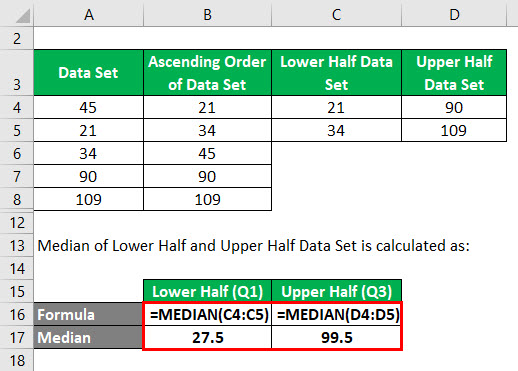

- Q1= 27.5
- Q3= 89
IQR é calculado utilizando a fórmula dada abaixo
IQR = Q3 – Q1
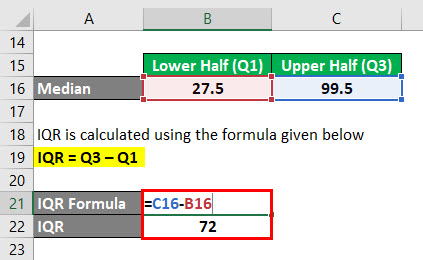

- IQR = 99.5 – 27.5
- IQR = 72
Outro inferior é calculado usando a fórmula dada abaixo
Outro inferior = Q1 – (1.5 * IQR)
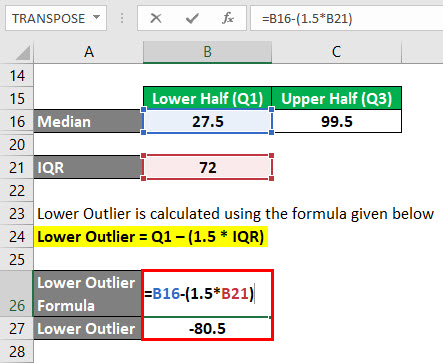

- Outli>Outli = 27.5 – (1,5 * 72)
- Lower Outlier = -80,5
Higher Outlier é calculado usando a fórmula dada abaixo
Higher Outlier = Q3 + (1.5 * IQR)
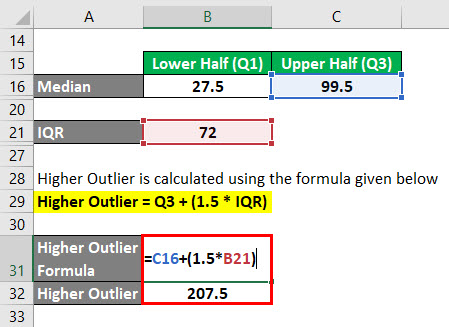

- Higher Outlier = 99,5 + (1.5 * 72)
- Higher Outlier = 207,5
Explicação
P>Passo 1: Organizar todos os valores do conjunto de dados dado em ordem ascendente.
Passo 2: Encontrar o valor mediano dos dados que são classificados. A mediana pode ser encontrada utilizando a seguinte fórmula. O cálculo seguinte dá-lhe simplesmente a posição do valor da mediana que reside no conjunto de datas.
Mediana = (n+1)/2
Onde n é o número total de dados disponíveis no conjunto de dados.
Passo 3: Encontrar o valor do Quartil inferior Q1 do conjunto de dados. Para o encontrar, utilizando o valor mediano, dividir o conjunto de dados em duas metades. A partir da metade inferior do conjunto de valores, encontrar a mediana desse conjunto inferior que é o valor Q1.
P>Passo 4: Encontrar o valor superior do Quartil Q3 a partir do conjunto de dados. É exactamente como o passo acima. Em vez da metade inferior, temos de seguir o mesmo procedimento a metade superior do conjunto de valores.
P>Passo 5: Encontrar o valor IQR do intervalo interquartil. Para encontrar o valor de Deduza Q1 de Q3.
IQR = Q3-Q1
P>Passo 6: Encontrar o valor do Extremo Interior. Um extremo que cai fora do lado inferior, que também pode ser chamado como um outlier menor. Multiplique o valor IQR por 1,5 e deduza este valor de Q1 dá-lhe o extremo Inferior Interior.
Lower Outlier =Q1 – (1,5 * IQR)
Etapa 7: Encontrar o valor Extremo Extremo Exterior. Um extremo que cai fora do lado superior que também pode ser chamado de outlier maior. Multiplique o valor do IQR por 1,5 e somando este valor com Q3 obtém-se o Extremo Extremo Extremo Extremo Exterior.
Outro Superior = Q3 + (1,5 * IQR)
P>Passo 8: Os valores que se situam fora destes extremos internos e externos são os valores exteriores para o conjunto de dados dado.
Fórmula de Fuga e Utilização de Outliers
Os Outliers são muito importantes em qualquer problema de análise de dados. Os outliers mostram inconsistência em qualquer conjunto de dados, uma vez que são definidos como os valores fora do comum no conjunto de dados de um para outro. Isto é muito útil para encontrar quaisquer falhas que tenham ocorrido no conjunto de dados. Porque quando se coloca um erro no conjunto de dados, este afecta a média e a mediana, pelo que pode obter grandes desvios no resultado se os Outliers estiverem no conjunto de dados. Assim, é essencial encontrar Outliers a partir do conjunto de dados a fim de evitar problemas graves na análise estatística.
Artigos Recomendados
Esta tem sido uma guia para a fórmula de Outliers. Aqui discutimos como calcular Outliers, juntamente com exemplos práticos e modelos Excel descarregáveis. Também pode consultar os seguintes artigos para saber mais –
- Guia para Fórmula de Médio Alcance
- Exemplos de Fórmula Salarial
- Calculador para Fórmula DPMO
- Como Calcular a Distribuição T?
- Fórmula de Desvio Quartil | Exemplos