Cálculo da Impedância
Em circuitos AC, a Lei de Ohm assume uma forma mais geral: E = I⋅Z, onde E é tensão e corrente Iis, como antes. O novo termo, Z, é impedância,uma combinação vectorial de:
- Resistência, R (em ohms), com quedas de tensão em fase com a corrente.
- Reactância indutiva, XL (em ohms), com gotas de tensão que conduzem a corrente em 90°.
- Reactância capacitiva, XC (em ohms), com gotas de voltagem a conduzir a corrente em 90°.
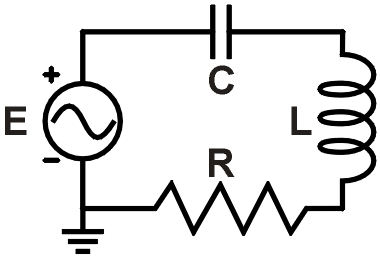
f = 6,4 kHz R = 120 Ω
L = 3,6 mH C = 0,38 μf
br>>p>p>Figure 1. Exemplo de circuito RLC >br>
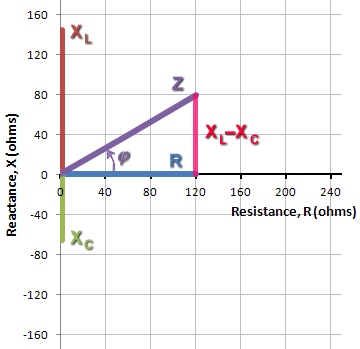
>br>>p> Figura 2. Soma vectorial de R e
XL-XC rendimentos Z
Das fórmulas para XL e XC, pode-se ver que as reactâncias dependem tanto dos valores dos componentes L e C,como da frequência AC, f:
![]() e
e 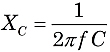
onde f é a frequência em Hertz (ou sec-1), L é indutância em Henries, e C iscapacitância em farads. Porque XL e XCare são 180° diferentes em fase, a reactância total X de uma série circuíte XL-XC.
Os usos familiares para a Lei de Ohm, tais como cálculos de série e circuitos paralelos, ainda se aplicam. No entanto, é agora necessário considerar as contribuições vectoriais concorrentes das resistências e reações.
Ângulos de fase e vectores
Vamos encontrar a impedância total do circuito na Figura 1. Usando as fórmulas acima:
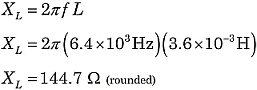 |
> | 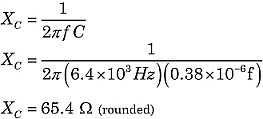 |
Construindo a impedância Z, a resistência contribui com o componente horizontal. O componente vertical é a diferença das reactâncias: XL-XC.Então, Z é a soma vectorial de R e XL-XC,como ilustrado na Figura 2.
Na Figura 2, visto que Z é a hipotenusa de um triângulo direito,podemos usar o teorema de Pitágoras e a geometria do triângulo direito para avaliar Z.
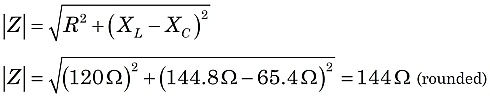
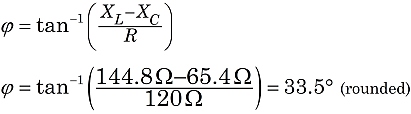
Assim, neste circuito, testemunharíamos o efeito de uma impedância de144 ohms, com a corrente a ficar atrás da tensão de alimentação num ângulo de fase de 33.5°.
Como pode adivinhar pela discussão acima, é bastante possível que as reactâncias indutivas e capacitivas sejam exactamente canceladas sob a combinação certa de L, C, e fvalues. Esta é uma condição muito importante conhecida como ressonância.