Obliczanie impedancji
W obwodach prądu zmiennego, prawo Ohma przyjmuje bardziej ogólną postać: E = I⋅Z, gdzie E to napięcie, a I to prąd, tak jak poprzednio. Nowy termin, Z, jest impedancją, kombinacją wektorową:
- Rezystancji, R (w omach), ze spadkami napięcia w fazie z prądem.
- Reaktancji indukcyjnej, XL (w omach), ze spadkami napięcia poprzedzającymi prąd o 90°.
- Reaktancja pojemnościowa, XC (w omach), ze skokami napięcia opóźniającymi prąd o 90°.
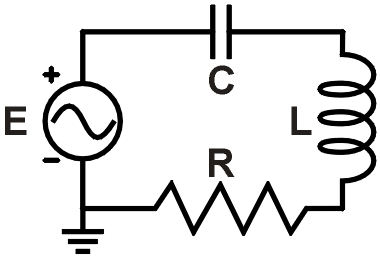
f = 6,4 kHz R = 120 Ω
L = 3,6 mH C = 0,38 μf
Rysunek 1. Przykładowy obwód RLC
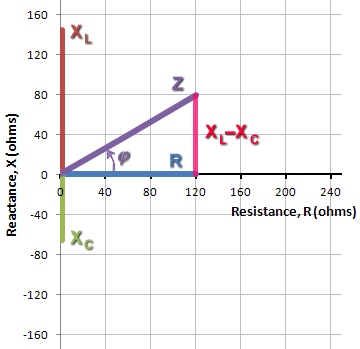
Rysunek 2. Suma wektorowa R i
XL-XC daje Z
Z wzorów dla XL i XC wynika, że reaktancje zależą zarówno od wartości składowych L i C, jak i od częstotliwości prądu zmiennego, f:
![]() i
i 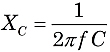
gdzie f to częstotliwość w hercach (lub sek-1), L to indukcyjność w Henrach, a C to pojemność w faradach. Ponieważ XL i X różnią się w fazie o 180°, całkowita reaktancja X obwodu szeregowego to XL-XC.
Znane zastosowania prawa Ohma, takie jak obliczanie obwodów szeregowych i równoległych, nadal mają zastosowanie. Jednakże, musisz teraz rozważyć konkurencyjne wkłady wektorowe z rezystancji i reaktancji.
Kąty fazowe i wektory
Znajdźmy całkowitą impedancję obwodu na rysunku 1. Korzystając z powyższych wzorów:
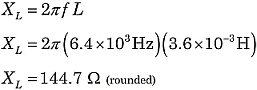 |
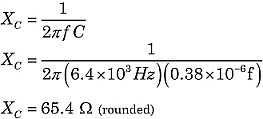 |
Konstruując impedancję Z, rezystor wnosi składową poziomą. Składowa pionowa jest różnicą reaktancji: XL-XC.Następnie, Z jest sumą wektorową R i XL-XC,jak pokazano na rysunku 2.
Na rysunku 2, widząc, że Z jest hipotensją trójkąta prostego, możemy użyć twierdzenia Pitagorasa i geometrii trójkąta prostego do oszacowania Z.
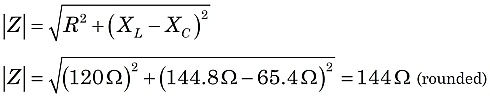
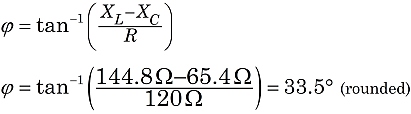
Więc, w tym obwodzie, będziemy świadkami efektu impedancji 144 ohm, z prądem opóźnionym w stosunku do napięcia zasilania przy kącie fazowym 33.5°.
Jak można się domyślić z powyższej dyskusji, jest całkiem możliwe, że reaktancje indukcyjne i pojemnościowe dokładnie się znoszą przy odpowiednich kombinacjach wartości L, C i f. Jest to bardzo ważny warunek znany jako rezonans.