Zdefiniowawszy, że funkcja logarytmiczna y = log b x jest funkcją odwrotną do funkcji wykładniczej y = b x, możemy teraz przejść do wykresów funkcji logarytmicznych, patrząc na związek między funkcjami wykładniczymi i logarytmicznymi.
Ale zanim przejdziemy do tematu wykresów funkcji logarytmicznych, ważne jest, abyśmy zapoznali się z następującymi terminami:
- Działka funkcji
Działka funkcji to zbiór wartości, które można zastąpić w funkcji, aby uzyskać akceptowalną odpowiedź.
- Przedział funkcji
Jest to zbiór wartości, które otrzymujemy po podstawieniu wartości z dziedziny do zmiennej.
- Asymptoty
Są trzy rodzaje asymptot, mianowicie: pionowa, pozioma i skośna. Asymptota pionowa to wartość x, przy której funkcja rośnie w pobliżu bez ograniczeń.
Asymptoty poziome to stałe wartości, do których f(x) zbliża się, gdy x rośnie bez ograniczeń. Asymptoty skośne to wielomiany pierwszego stopnia, do których f(x) zbliża się, gdy x rośnie bez ograniczeń.
Jak wykreślić funkcje logarytmiczne?
Wykres funkcji logarytmicznej można zrobić analizując wykres funkcji wykładniczej, a następnie zamieniając miejscami x i y.
Wykres funkcji wykładniczej f (x) = b x lub y = b x zawiera następujące cechy:
- Działką funkcji wykładniczej są liczby rzeczywiste (-nieskończoność, nieskończoność).
- Przedziałem są również dodatnie liczby rzeczywiste (0, nieskończoność)
- Wykres funkcji wykładniczej zwykle przechodzi przez punkt (0, 1). Oznacza to, że punkt y – intercept znajduje się w punkcie (0, 1).
- Wykres funkcji wykładniczej f(x) = b x ma asymptotę poziomą w punkcie y = 0.
- Wykres wykładniczy zmniejsza się od lewej do prawej, jeśli 0 < b < 1, a ten przypadek jest znany jako rozkład wykładniczy.
- Jeśli podstawa funkcji f(x) = b x jest większa niż 1, to jej wykres będzie wzrastał od lewej do prawej i jest nazywany wzrostem wykładniczym.
Patrząc na powyższe cechy po kolei, możemy podobnie wydedukować cechy funkcji logarytmicznych w następujący sposób:
- Funkcja logarytmiczna będzie miała dziedzinę jako (0, nieskończoność).
- Przedział funkcji logarytmicznej to (-nieskończoność, nieskończoność).
- Wykres funkcji logarytmicznej przechodzi przez punkt (1, 0), który jest odwrotnością punktu (0, 1) dla funkcji wykładniczej.
- Wykres funkcji logarytmicznej ma asymptotę pionową przy x = 0.
- Wykres funkcji logarytmicznej będzie malał od lewej do prawej, jeśli 0 < b < 1.
- A jeśli podstawa funkcji jest większa od 1, b > 1, to wykres będzie wzrastał od lewej do prawej.
Jak wykreślić wykres podstawowej funkcji logarytmicznej?
Podstawowa funkcja logarytmiczna to zazwyczaj funkcja bez przesunięcia w poziomie lub w pionie.
Oto kroki tworzenia wykresu podstawowej funkcji logarytmicznej.
- Ponieważ wszystkie funkcje logarytmiczne przechodzą przez punkt (1, 0), zlokalizujemy i umieścimy kropkę w tym punkcie.
- Aby krzywa nie dotykała osi y, rysujemy asymptotę przy x = 0.
- Jeśli podstawa funkcji jest większa niż 1, zwiększamy krzywą od lewej do prawej. Podobnie, jeśli podstawa jest mniejsza niż 1, zmniejszamy krzywą od lewej do prawej.
Przyjrzyjrzyjmy się teraz następującym przykładom:
Przykład 1
Zrób wykres funkcji logarytmicznej f(x) = log 2 x oraz podaj zakres i dziedzinę funkcji.
Rozwiązanie
- Oczywiście, funkcja logarytmiczna musi mieć dziedzinę i przedział (0, nieskończoność) oraz (-nieskończoność, nieskończoność)
- Ponieważ funkcja f(x) = log 2 x jest większa od 1, będziemy zwiększać naszą krzywą od lewej do prawej, jak pokazano poniżej.
- Nie możemy zobaczyć pionowej asymptoty przy x = 0, ponieważ jest ona zasłonięta przez oś y.
Przykład 2
Narysuj wykres y = log 0,5 x
Rozwiązanie
- Postaw kropkę w punkcie (1, 0). Wszystkie krzywe logarytmiczne przechodzą przez ten punkt.
- Narysuj asymptotę przy x = 0.
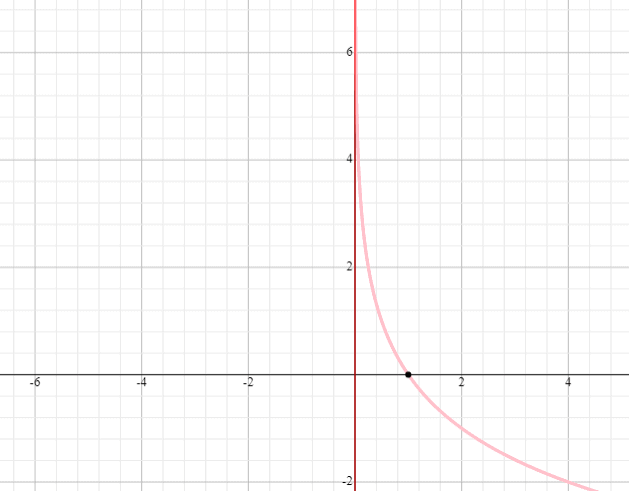
- Ponieważ podstawa funkcji y = log 5 x jest mniejsza od 1, będziemy zmniejszać naszą krzywą od lewej do prawej.
- Funkcja y = log 5 x będzie miała również (0, nieskończoność) i (-nieskończoność, nieskończoność) jako dziedzinę i przedział.
Graphing a logarithmic function with a horizontal shift
Funkcje logarytmiczne z przesunięciem poziomym mają postać f(x) = log b (x + h) lub f (x) = log b (x – h), gdzie h = przesunięcie poziome. Znak przesunięcia poziomego określa kierunek przesunięcia. Jeśli znak jest dodatni, przesunięcie będzie ujemne, a jeśli znak jest ujemny, przesunięcie stanie się dodatnie.
Poprzez zastosowanie przesunięcia poziomego cechy funkcji logarytmicznej zmieniają się w następujący sposób:
- Przecinek x przesuwa się w lewo lub w prawo o stałą odległość równą h.
- Pionowa asymptota przesuwa się na odległość równą h.
- Zmienia się również dziedzina funkcji.
Przykład 3
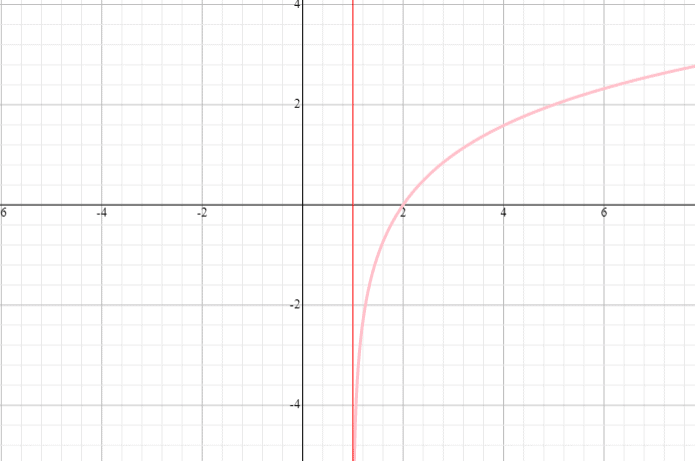
Narysuj wykres funkcji f(x) = log 2 (x + 1) oraz podaj dziedzinę i przedział funkcji.
Rozwiązanie
⟹ Dziedzina: (- 1, nieskończoność)
⟹ Zakres: (-infinity, infinity)
Przykład 4
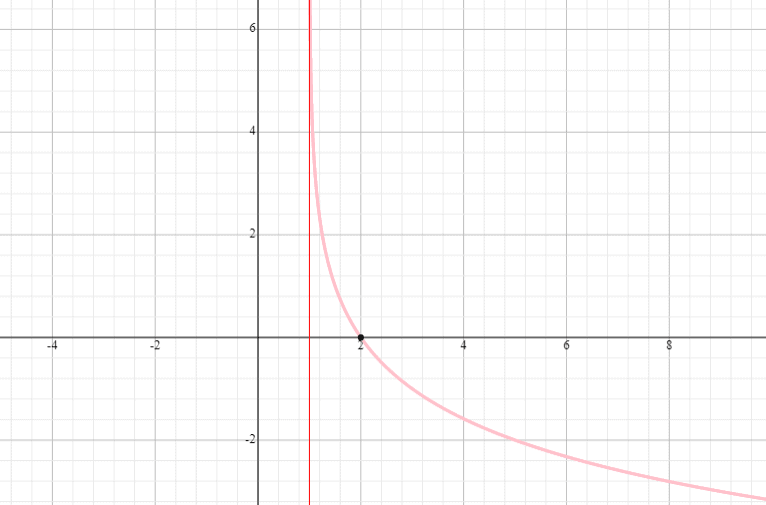
Grafika y = log 0,5 (x – 1) oraz podanie dziedziny i zakresu.
Rozwiązanie
⟹ Dziedzina: (1, nieskończoność)
⟹ Zakres: (-nieskończoność, nieskończoność)
Jak wykreślić funkcję z przesunięciem pionowym?
Funkcja logarytmiczna z przesunięciem zarówno poziomym, jak i pionowym ma postać f(x) = log b (x) + k, gdzie k = przesunięcie pionowe.
Przesunięcie pionowe wpływa na cechy funkcji w następujący sposób:
- Przecinek x przesunie się albo w górę, albo w dół o stałą odległość k
Przykład 5
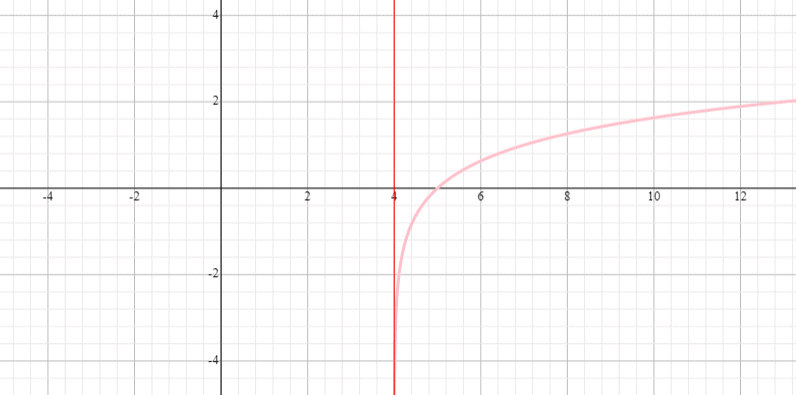
Zrób wykres funkcji y = log 3 (x – 4) i podaj przedział i dziedzinę funkcji.
Rozwiązanie
⟹ Dziedzina: (0, nieskończoność)
⟹ Zakres: (-nieskończoność, nieskończoność)
Funkcje z przesunięciem zarówno poziomym jak i pionowym
Funkcja logarytmiczna z przesunięciem zarówno poziomym jak i pionowym ma postać (x) = log b (x + h) + k, gdzie k i h to odpowiednio przesunięcia pionowe i poziome.
Przykład 6
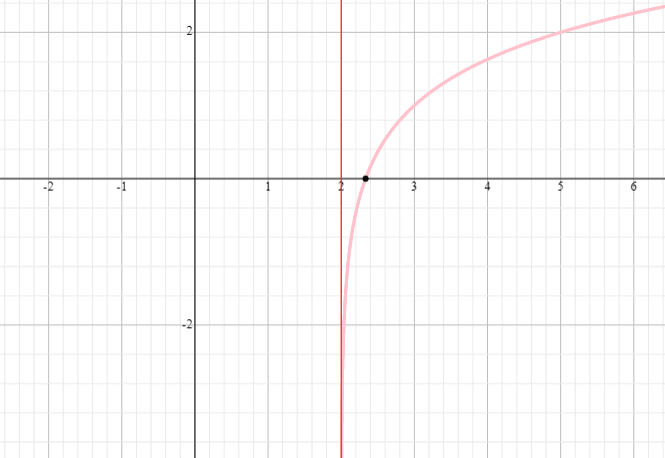
Zrób wykres funkcji logarytmicznej y = log 3 (x – 2) + 1 oraz znajdź dziedzinę i przedział tej funkcji.
Rozwiązanie
⟹ Dziedzina: (2, nieskończoność)
⟹ Zakres: (-nieskończoność, nieskończoność)
Przykład 7
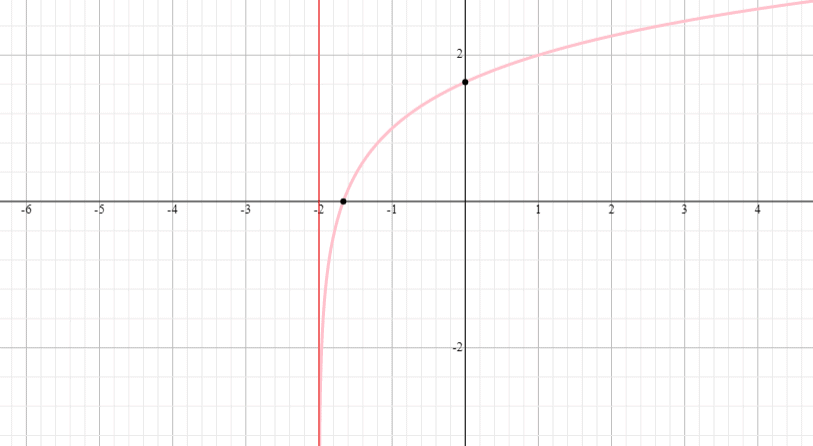
Zaprezentuj wykres funkcji logarytmicznej y = log 3 (x + 2) + 1 oraz znajdź dziedzinę i przedział tej funkcji.
Rozwiązanie
⟹ Dziedzina: (- 2,nieskończoność)
⟹ Zakres: (-nieskończoność, nieskończoność)
Poprzednia lekcja | Strona główna | Następna lekcja
.