Nelle applicazioni ingegneristiche, incontriamo spesso funzioni i cui valori cambiano bruscamente a determinati valori di tempo t. Un esempio comune è quando una tensione viene accesa o spenta in un circuito elettrico a un determinato valore di tempo t.
Più tardi, in questa pagina…
Funzione a gradino unitario spostato
Impulso rettangolare
Il valore di t = 0 è solitamente preso come un tempo conveniente per accendere o spegnere la tensione data.
Il processo di commutazione può essere descritto matematicamente dalla funzione chiamata funzione a passo unitario (altrimenti nota come funzione di Heaviside da Oliver Heaviside).
La funzione a passo unitario
Definizione: La funzione di passo unitario, `u(t)`, è definita come
`u(t)={: {(0, t < 0), (1, t > 0) :}`
Ovvero, u è una funzione del tempo t, e u ha valore zero quando il tempo è negativo (prima di premere l’interruttore); e valore uno quando il tempo è positivo (da quando premiamo l’interruttore).
Grafico di `f(t)=u(t)`, la funzione a passo unitario.
Valore a t = 0?
In alcuni libri di testo vedrete la funzione a passo unitario definita come avente valore 1 a t = 0, come segue:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
Indicheremmo la discontinuità sul nostro grafico in questo modo:
Grafico di `f(t)=u(t)`, la funzione passo unitario, con `f(0) = 1`.
Inoltre, a volte vedrai il valore dato come `f(0) = 0.5`.
In questo lavoro, non fa molta differenza per i nostri calcoli, quindi continueremo ad usare la prima interpretazione, e disegneremo i nostri grafici di conseguenza.
Funzione a passo unitario spostata
In molti circuiti, le forme d’onda sono applicate ad intervalli specifici diversi da `t=0`. Una tale funzione può essere descritta usando la funzione a passo unitario spostata (o ritardata).
Definizione di Shifted Unit Step Function
Una funzione che ha valore `0` fino al tempo `t = a` e successivamente ha valore `1`, si scrive:
`u(t-a)={: (0, se, t < a), (1, se, t > a) :}`
Esempio 1 – Funzione a passo unitario spostata
`f(t) = u(t – 3)`
Il equazione significa che f(t) ha valore di `0` quando `t < 3` e `1` quando `t > 3`.
Lo schizzo della forma d’onda è il seguente:
Grafico di `f(t)=u(t-3)`, una funzione a passo unitario spostata.
Impulso rettangolare
Una situazione comune in un circuito è che una tensione sia applicata in un particolare momento (diciamo t = a) e rimossa successivamente, a t = b (diciamo). Scriviamo una tale situazione usando funzioni a passo unitario come:
`V(t) = u(t – a) – u(t – b)`
Questa tensione ha forza `1`, durata `(b – a)`.
Esempio 2 – Impulso rettangolare
Il grafico di `V(t) = u(t – 1.2) – u(t – 3.8)` è il seguente. Qui, la durata è `3.8 – 1.2 = 2.6`.
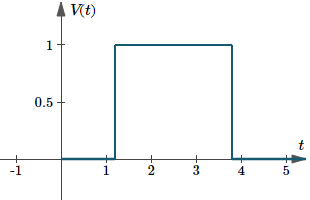
Grafico di `V(t)=u(t-1.2)-u(t-3.8)`, un esempio di impulso rettangolare.
Esercizi
Hai bisogno di carta grafica?
Scrivi le seguenti funzioni in termini di funzioni di passo unitario. Abbozza ogni forma d’onda.
(a) Una sorgente di 12 V viene accesa a t = 4 s.
Risposta
Siccome la tensione viene accesa a t = 4, dobbiamo usare u(t – 4). Moltiplichiamo per 12, dato che questa è la tensione.
Scriviamo la funzione come segue:
`V(t)=12-u(t-4)`.
Ecco il grafico:
Graph of `V(t)=12-u(t-4)`, a shifted step function.
(b) `V(t)={{: (1, 0 < t < a),(0, t > a) :}`
(Assumere a > 0.)
Risposta
In parole, la tensione ha valore `1` fino al tempo `t = a`. Poi si spegne.
Abbiamo una situazione di “impulso rettangolare” e dobbiamo usare questa formula:
`V(t) = u(t – a) – u(t – b)`
Nel nostro esempio, l’impulso inizia a `t = 0`, quindi usiamo `u(t)`, e finisce a `t = a`, quindi usiamo `u(t – a)`.
Quindi la funzione richiesta è:
`V(t)=1-` `=u(t)-u(t-a)`
Grafico di `V(t)=u(t)-u(t-a)`, una funzione a passo unitario spostato.
(c) Un ciclo di un’onda quadra, `f(0) = 4`, ampiezza = `4`, periodo = `2` secondi.
Se l’intera onda ha periodo `2`, ed è un’onda quadra, allora significa che per metà del tempo, il valore è (positivo) `4` e l’altra metà è `-4`.
Quindi per il primo secondo, ha valore `4`, per il secondo secondo, il valore della funzione è `-4`.
Scriviamo questo, usando la formula “impulso rettangolare” di prima:
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
Il grafico di questo primo ciclo è:
Grafico di `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, un’onda quadra.
(d) La funzione di Rampa unitaria (cioè`f(t) = t` per `t > 0`)
Risposta
La funzione rampa unitaria ha pendenza `1` , partendo da `t = 0` , e passa per `(0, 0)`.
Quindi la funzione di tensione è data da:
`V(t) = t – u(t)`
Il grafico della funzione è:
Grafico di `V(t)=t – u(t)`, la funzione di rampa unitaria.
(e) Un ciclo di una forma d’onda a dente di sega (es.e. `f(t)=a/b t` per `0 < t < b`. Assumere `a > 0`.)
Risposta
Il nostro grafico inizia a `t = 0` e ha pendenza `a / b`. Finisce a `t = b`.
Quindi la nostra funzione sarà:
`f(t)=a/b t – {u(t)-u(t-b)}`
Il grafico della nostra funzione:
Grafico di `f(t)=a/b t – {u(t)-u(t-b)}`, una forma d’onda a dente di sega.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t 5) :}`
Risposta
In questo esempio, la nostra funzione è `V(t) = 2t + 8` che ha pendenza `2` e `V`-intercetta `8`.
Il segnale è acceso solo tra `t = 3` e `t = 5`. Il resto del tempo è spento.
Quindi la nostra funzione di tensione sarà:
`V(t) ` `= (2t+8) -{u(t – 3)- u(t – 5)}`
Il grafico è il seguente:
Grafico di `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}`. La linea tratteggiata è `V(t) = 2t + 8`.
top
Cerca IntMath
Solutore di calcolo online
Questo risolutore di calcolo può risolvere una vasta gamma di problemi matematici.
Vai a: Risolutore di calcolo online