Il campionamento è definito come, “Il processo di misurazione dei valori istantanei di un segnale a tempo continuo in una forma discreta.”
Campione è un pezzo di dati preso da tutti i dati che sono continui nel dominio del tempo.
Quando una fonte genera un segnale analogico e se questo deve essere digitalizzato, avendo 1s e 0s cioè, Alto o Basso, il segnale deve essere discretizzato nel tempo. Questa discretizzazione del segnale analogico è chiamata campionamento.
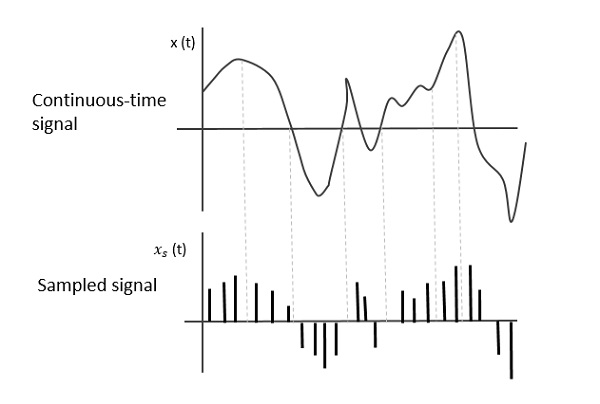
La figura seguente indica un segnale a tempo continuo x (t) e un segnale campionato xs (t). Quando x (t) viene moltiplicato per un treno di impulsi periodici, si ottiene il segnale campionato xs (t).
Tasso di campionamento
Per discretizzare i segnali, lo spazio tra i campioni deve essere fissato. Questo intervallo può essere definito come periodo di campionamento Ts.
$Sampling \: Frequenza = \frac{1}{T_{s}} = f_s$
dove,
-
$T_{s}$ è il tempo di campionamento
-
$f_{s}$ è la frequenza di campionamento o il tasso di campionamento
La frequenza di campionamento è il reciproco del periodo di campionamento. Questa frequenza di campionamento può essere chiamata semplicemente frequenza di campionamento. La frequenza di campionamento denota il numero di campioni presi al secondo, o per un insieme finito di valori.
Per un segnale analogico da ricostruire dal segnale digitalizzato, la frequenza di campionamento dovrebbe essere altamente considerata. La frequenza di campionamento dovrebbe essere tale che i dati nel segnale del messaggio non dovrebbero essere persi né sovrapposti. Quindi, è stato fissato un tasso per questo, chiamato tasso di Nyquist.
Tasso di Nyquist
Supponiamo che un segnale sia a banda limitata con nessuna componente di frequenza superiore a W Hertz. Ciò significa che W è la frequenza più alta. Per un tale segnale, per una riproduzione efficace del segnale originale, la frequenza di campionamento dovrebbe essere il doppio della frequenza più alta.
Che significa,
$f_{S} = 2W$
dove,
-
$f_{S}$ è la frequenza di campionamento
-
W è la frequenza più alta
Questo tasso di campionamento è chiamato tasso di Nyquist.
Un teorema chiamato, Teorema del campionamento, è stato enunciato sulla teoria di questo tasso di Nyquist.
Teorema del campionamento
Il teorema del campionamento, chiamato anche teorema di Nyquist, fornisce la teoria della frequenza di campionamento sufficiente in termini di larghezza di banda per la classe di funzioni che sono limitate in banda.
Il teorema del campionamento afferma che “un segnale può essere riprodotto esattamente se viene campionato alla velocità fs che è maggiore del doppio della frequenza massima W.”
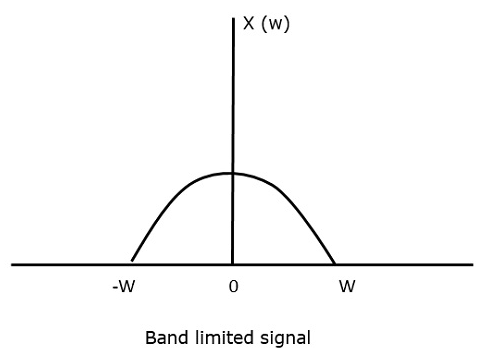
Per capire questo teorema del campionamento, consideriamo un segnale limitato in banda, cioè, un segnale il cui valore non è zero tra alcuni -W e W Hertz.
Un tale segnale è rappresentato come $x(f) = 0 per |f\lvert > W$
Per il segnale a tempo continuo x (t), il segnale a banda limitata nel dominio della frequenza, può essere rappresentato come mostrato nella figura seguente.
Abbiamo bisogno di una frequenza di campionamento, una frequenza alla quale non ci dovrebbe essere perdita di informazione, anche dopo il campionamento. Per questo, abbiamo il tasso di Nyquist che la frequenza di campionamento dovrebbe essere due volte la frequenza massima. È la frequenza critica di campionamento.
Se il segnale x(t) viene campionato sopra la frequenza di Nyquist, il segnale originale può essere recuperato, e se viene campionato sotto la frequenza di Nyquist, il segnale non può essere recuperato.
La figura seguente spiega un segnale, se campionato a una velocità superiore a 2w nel dominio della frequenza.
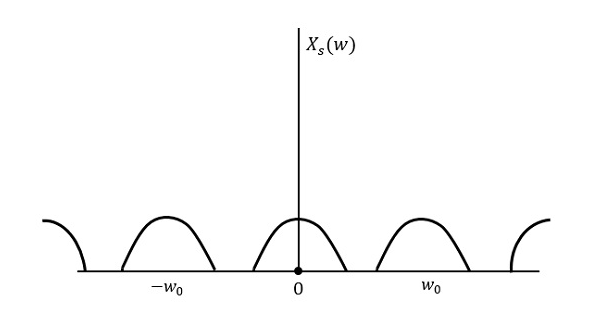
La figura precedente mostra la trasformata di Fourier di un segnale $x_{s}(t)$. Qui, l’informazione è riprodotta senza alcuna perdita. Non c’è mescolanza e quindi il recupero è possibile.
La trasformata di Fourier del segnale $x_{s}(t)$ è
$X_{s}(w) = \frac{1}{T_{s}}}sum_{n = – \infty}^\infty X(w-nw_0)$
dove $T_{s}$ = Periodo di campionamento e $w_{0} = \frac{2 \pi}{T_s}$
Vediamo cosa succede se la frequenza di campionamento è uguale al doppio della frequenza più alta (2W)
Questo significa,
$f_{s} = 2W$
dove,
-
$f_{s}$ è la frequenza di campionamento
-
W è la frequenza più alta
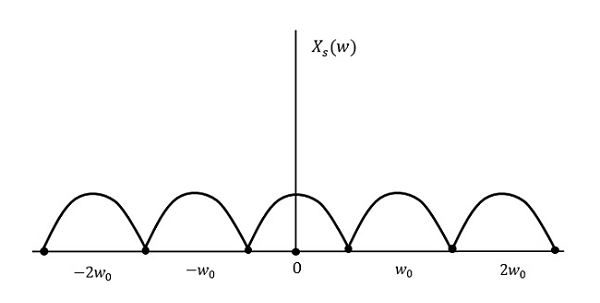
Il risultato sarà come mostrato nella figura precedente. L’informazione viene sostituita senza alcuna perdita. Quindi, questo è anche un buon tasso di campionamento.
Ora, guardiamo la condizione,
$f_{s} Il modello risultante sarà come la figura seguente.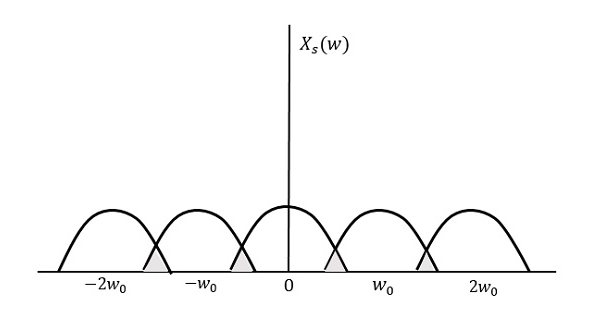
Possiamo osservare dal modello di cui sopra che la sovrapposizione di informazioni è fatta, che porta alla miscelazione e alla perdita di informazioni. Questo fenomeno indesiderato di sovrapposizione è chiamato Aliasing.
Aliasing
L’Aliasing può essere definito come “il fenomeno di una componente ad alta frequenza nello spettro di un segnale che assume l’identità di una componente a bassa frequenza nello spettro della sua versione campionata.”
Le misure correttive adottate per ridurre l’effetto dell’Aliasing sono –
-
Nella sezione di trasmissione del PCM, un filtro passa basso anti-aliasing è impiegato, prima del campionatore, per eliminare le componenti ad alta frequenza, che sono indesiderate.
-
Il segnale che viene campionato dopo il filtraggio, viene campionato a una frequenza leggermente superiore alla frequenza di Nyquist.
Questa scelta di avere una frequenza di campionamento superiore alla frequenza di Nyquist, aiuta anche nella progettazione del filtro di ricostruzione al ricevitore.
Campo di applicazione della trasformata di Fourier
Si osserva generalmente che si cerca l’aiuto delle serie di Fourier e delle trasformate di Fourier per analizzare i segnali e anche per dimostrare i teoremi. Questo perché –
-
La trasformata di Fourier è l’estensione della serie di Fourier per segnali non periodici.
-
La trasformata di Fourier è un potente strumento matematico che aiuta a visualizzare i segnali in diversi domini e aiuta ad analizzare i segnali facilmente.
-
Ogni segnale può essere decomposto in termini di somma di seni e coseni usando questa trasformata di Fourier.
Nel prossimo capitolo, discutiamo il concetto di quantizzazione.