Contenuto
Metodo di Newton
La verità è troppo complicata per permettere solo approssimazioni.
– John Von Neumann
Trovare una soluzione con la geometria
Il metodo di Newton per risolvere le equazioni è un altro metodo numerico per risolvere un’equazione $f(x) = 0$. Si basa sulla geometria di una curva, usando le linee tangenti ad una curva. Come tale, richiede il calcolo, in particolare la differenziazione.
Rapidamente, l’idea del metodo di Newton è la seguente. Cerchiamo una soluzione di $f(x) = 0$. Cioè, vogliamo trovare il punto rosso tratteggiato nell’immagine qui sotto.
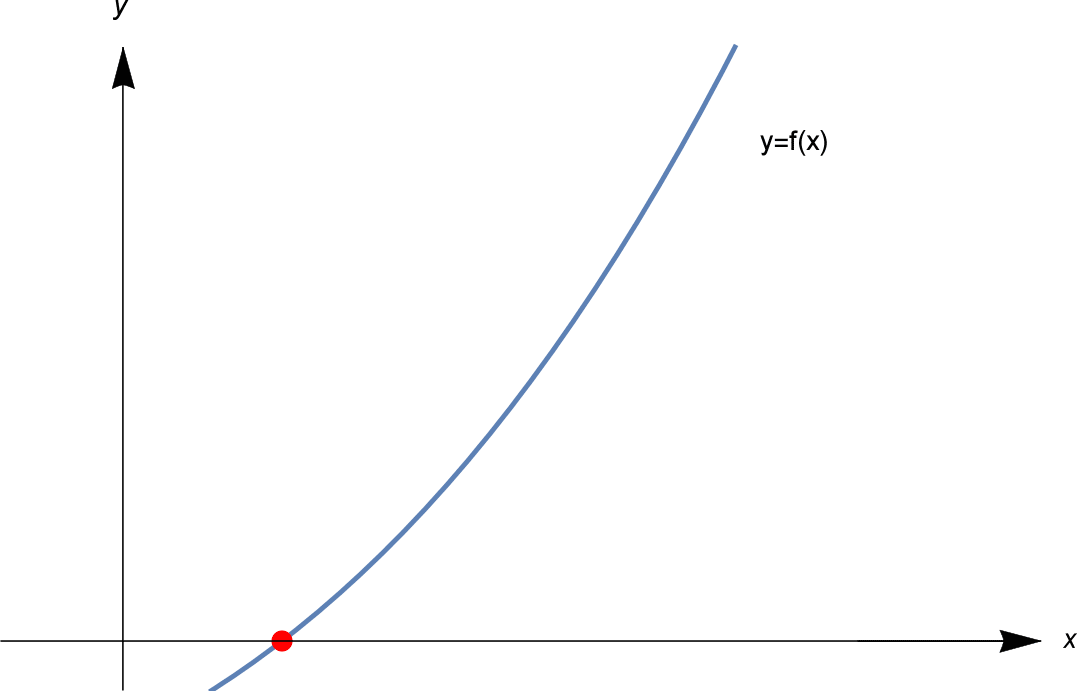
Partiamo con un’ipotesi iniziale $x_1$. Calcoliamo $f(x_1)$. Se $f(x_1) = 0$, siamo molto fortunati e abbiamo una soluzione. Ma molto probabilmente $f(x_1)$ non è zero. Lasciamo che $f(x_1) = y_1$, come mostrato.
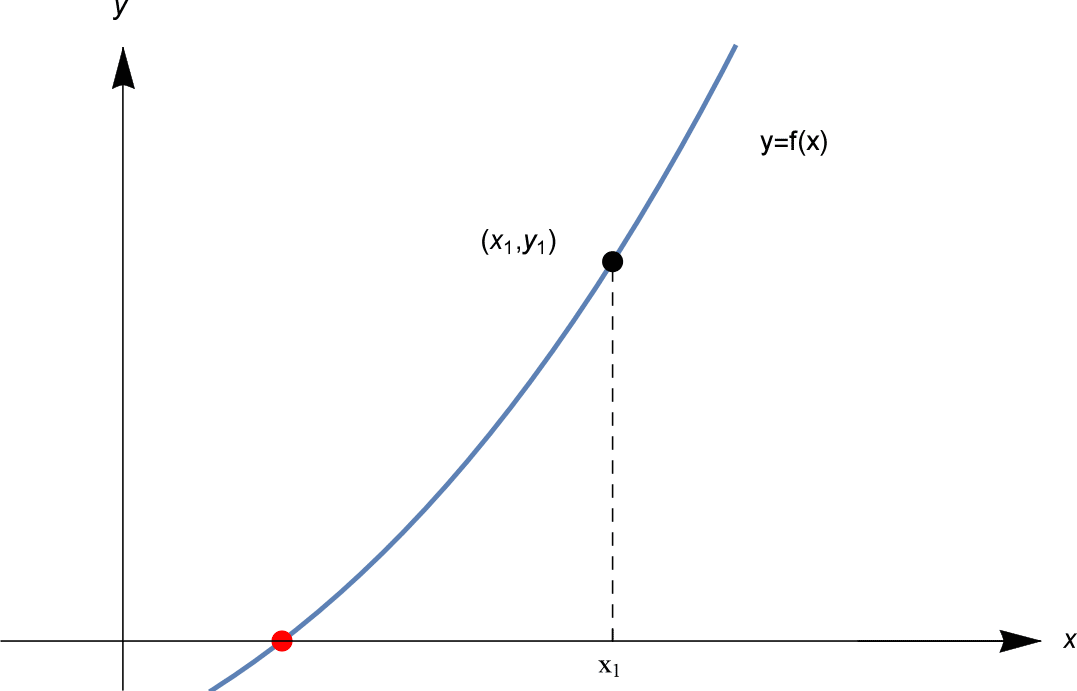
Tentiamo ora un’ipotesi migliore. Come trovare questa ipotesi migliore? Il trucco del metodo di Newton è di disegnare una linea tangente al grafico $y=f(x)$ nel punto $(x_1, y_1)$. Vedi sotto.
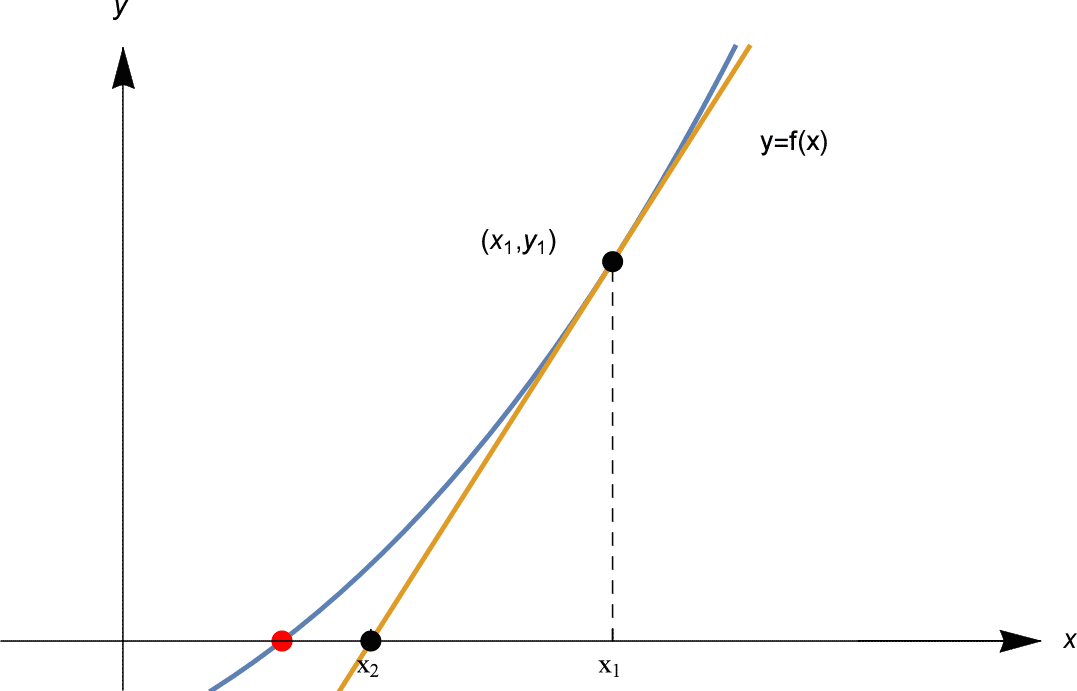
Questa linea tangente è una buona approssimazione lineare a $f(x)$ vicino a $x_1$, quindi la nostra prossima ipotesi $x_2$ è il punto in cui la linea tangente interseca l’asse $x$, come mostrato sopra.
Proseguiamo con lo stesso metodo. Calcoliamo $y_2 = f(x_2)$; se è zero, abbiamo finito. Se non lo è, allora tracciamo la linea tangente a $y=f(x)$ in $(x_2, y_2)$, e la nostra prossima ipotesi $x_3$ è il punto in cui questa linea tangente interseca l’asse $x$. Vedi sotto.
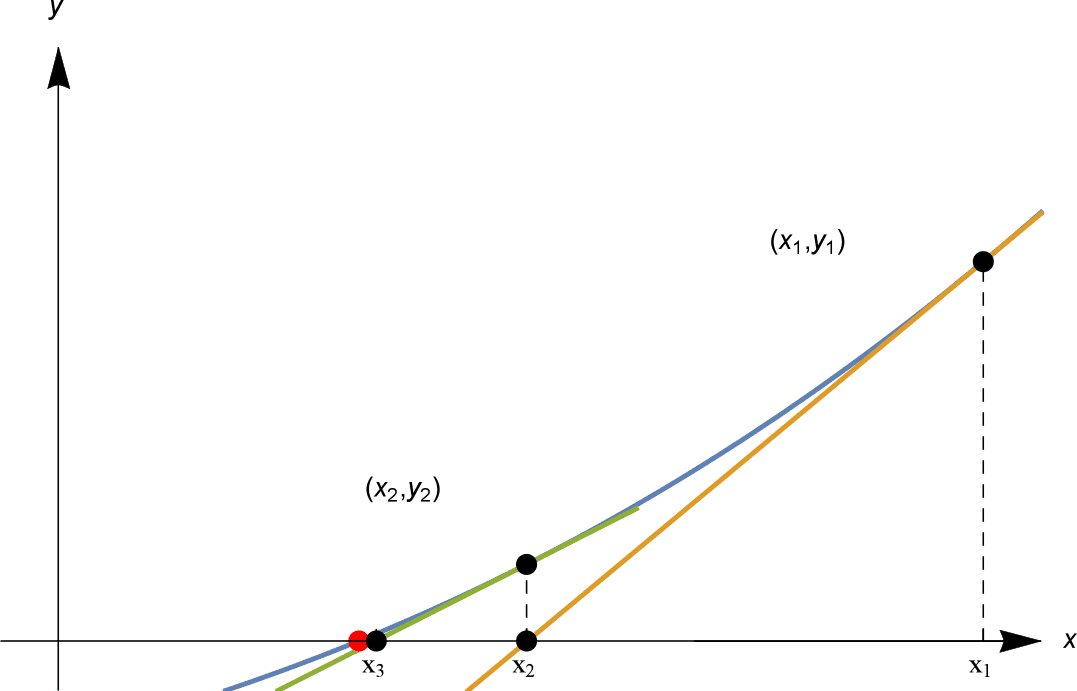
Nella figura mostrata, $x_1, x_2, x_3$ si avvicinano rapidamente al punto rosso della soluzione!
Continuando in questo modo, troviamo punti $x_1, x_2, x_3, x_4, \ldots$ che approssimano una soluzione. Questo metodo per trovare una soluzione è il metodo di Newton.
Come vedremo, il metodo di Newton può essere un metodo molto efficiente per approssimare la soluzione di un’equazione – quando funziona.
Il calcolo chiave
Come ha appena mostrato la nostra introduzione, il calcolo chiave in ogni passo del metodo di Newton è trovare dove la linea tangente a $y=f(x)$ nel punto $(x_1, y_1)$ interseca l’asse $x$. La linea tangente che stiamo cercando passa per il punto $(x_1, y_1)$ e ha pendenza $f'(x_1)$.
Ricordiamo che, data la pendenza $m$ di una retta, e un punto $(x_0, y_0)$ su di essa, la retta ha equazione
\
Nella nostra situazione, la retta ha pendenza $f'(x_1)$, e passa per $(x_1, y_1)$, quindi ha equazione
\
Vedi il diagramma sotto.
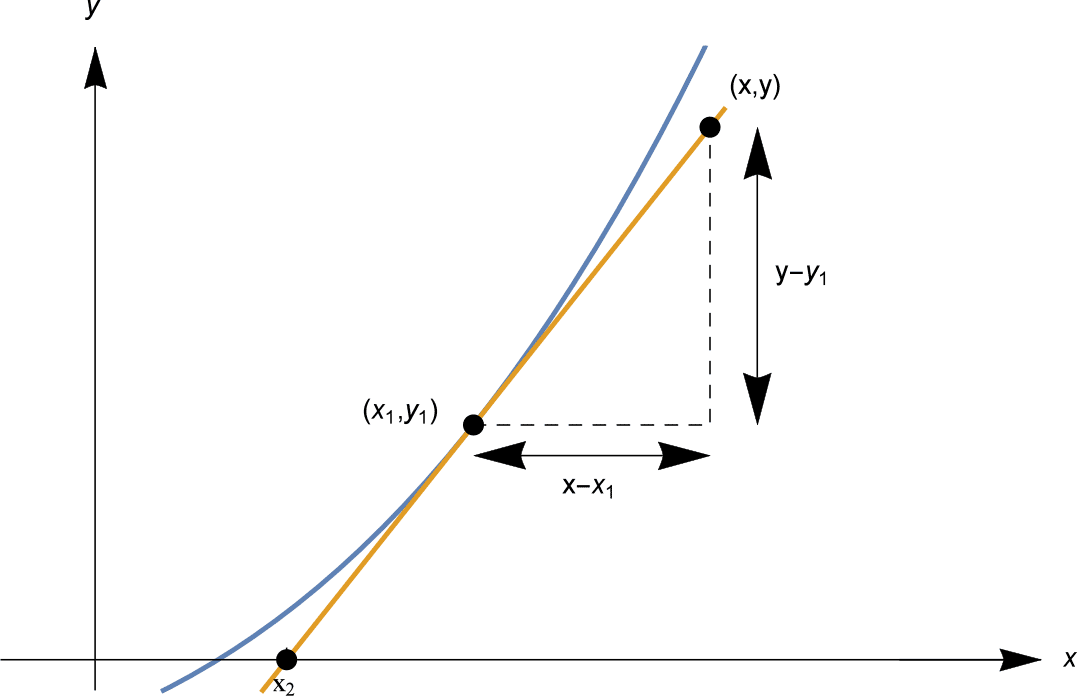
Fissando $y=0$, troviamo l’intercetta di $x$ come
L’algoritmo
Ora possiamo descrivere il metodo di Newton algebricamente. Partendo da $x_1$, il calcolo precedente mostra che se costruiamo la linea tangente al grafico $y=f(x)$ a $x=x_1$, questa linea tangente ha $x$-intercetta data da
\
Poi, partendo da $x_2$ eseguiamo lo stesso calcolo, e otteniamo la prossima approssimazione $x_3$ come
\
Lo stesso calcolo vale per ogni tappa: quindi dalla $n
Metodo di Newton
Lascia che $f: \mathbb{R} \mathbb{R}$ sia una funzione differenziabile. Cerchiamo una soluzione di $f(x) = 0$, partendo da una stima iniziale $x = x_1$.
Al passo $n$, dato $x_n$, calcoliamo la prossima approssimazione $x_{n+1}$ per
Alcuni commenti su questo algoritmo:
- Spesso il metodo di Newton funziona estremamente bene, e gli $x_n$ convergono rapidamente verso una soluzione. Tuttavia, è importante notare che il metodo di Newton non funziona sempre. Diverse cose possono andare storte, come vedremo tra poco.
- Nota che se $f(x_n) = 0$, in modo che $x_n$ sia una soluzione esatta di $f(x) = 0$, allora l’algoritmo dà $x_{n+1} = x_n$, e infatti tutti $x_n, x_{n+1}, x_{n+2}, x_{n+3}, \ldots$ saranno uguali. Se avete una soluzione esatta, il metodo di Newton rimarrà su quella soluzione!
- Mentre il metodo della bisezione richiede solo che $f$ sia continua, il metodo di Newton richiede che la funzione $f$ sia differenziabile. Questo è necessario perché $f$ abbia una linea tangente.
Utilizzando il metodo di Newton
Come abbiamo fatto con il metodo della bisezione, approssimiamo alcune costanti ben note.
Esempio
Utilizza il metodo di Newton per trovare una soluzione approssimata di $x^2 – 2 = 0$, partendo da una stima iniziale $x_1 =2$. Dopo 4 iterazioni, quanto è vicina l’approssimazione a $\sqrt{2}$?
Soluzione
Sia $f(x) = x^2 – 2$, quindi $f'(x) = 2x$. Al passo 1, abbiamo $x_1 = 2$ e calcoliamo $f(x_1) = 2^2 – 2 = 2$ e $f'(x_1) = 4$, quindi
\
Al passo 2, da $x_2 = \frac{3}{2}$ calcoliamo $f(x_2) = \frac{1}{4}$ e $f'(x_2) = 3$, quindi
\
Al passo 3, da $x_3 = \frac{17}{12}$ abbiamo $f(x_3) = \frac{1}{144}$ e $f'(x_3) = \frac{17}{6}$, quindi
Al passo 4 da $x_4 = \frac{577}{408}$ calcoliamo $f(x_4) = \frac{1}{166,464}$ e $f'(x_4) = \frac{577}{204}$, quindi
\
In effetti, con 12 decimali $\sqrt{2} \sim 1,414213562373$. Quindi dopo 4 iterazioni, la soluzione approssimata $x_5$ concorda con $sqrt{2}$ a 11 cifre decimali. La differenza tra $x_5$ e $sqrt{2}$ è
Il metodo di Newton nell’esempio precedente è molto più veloce dell’algoritmo di bisezione! In sole 4 iterazioni abbiamo 11 decimali di precisione! La seguente tabella illustra quante cifre decimali di precisione abbiamo in ogni $x_n$.
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
| # precisione decimale in | $0$ | $0$ | $2$ | $5$ | $11$ | $23$ | $47$ |
Il numero di decimali di precisione raddoppia approssimativamente ad ogni iterazione!
Esercizio 10
(Più difficile.) Questo problema studia questo raddoppio della precisione:
- Prima calcola che $x_{n+1} = \frac{x_n}{2} + \frac{1}{x_n}$ e che, se $y_n = x_n – \sqrt{2}$, allora $y_{n+1} = \frac{y_n^2}{2(\sqrt{2} + y_n)}$.
- Si dimostri che, se $x_1 > 0$ (rispettivamente $x_1 \sqrt{2}$ (rispettivamente. $x_n
- Mostrare che se $0
- Mostrare che, per $n \geq 2$, se $x_n$ differisce da $\sqrt{2}$ di meno di $10^{-k}$, allora $x_{n+1}$ differisce da $\sqrt{2}$ di meno di $10^{-2k}$.
Esempio
Trova un’approssimazione a $\pi$ usando il metodo di Newton per risolvere $\sin x = 0$ per 3 iterazioni, partendo da $x_1=3$. Con quanti decimali la soluzione approssimata è accurata?
Soluzione
Lascia che $f(x) = \sin x$, quindi $f'(x) = \cos x$. Calcoliamo direttamente $x_2, x_3, x_4$ usando la formula
\
Calcoliamo direttamente ogni $x_n$ a 25 cifre decimali, per 3 iterazioni:
\
A 25 cifre decimali, $\pi = 3.1415926535897932384626433$; $x_4$ concorda con 24 posizioni.
Nell’esempio di cui sopra, la convergenza è ancora più rapida che nel nostro esempio di $sqrt{2}$. Il numero di accuratezza dei decimali triplica all’incirca ad ogni iterazione!
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | |
| # precisione decimale in $x_n$ | $0$ | $2$ | $9$ | $24$ | $87$ |
Esercizio 11
Trova tutte le soluzioni dell’equazione $\cos x = x$ a 9 cifre decimali utilizzando il metodo di Newton. Confronta la convergenza con quella ottenuta con il metodo della bisezione nell’esercizio 5.
Cosa può andare storto
Mentre il metodo di Newton può dare approssimazioni fantasticamente buone ad una soluzione, diverse cose possono andare male. Esaminiamo ora alcuni di questi comportamenti meno fortunati.
Il primo problema è che $x_n$ può anche non essere definito!
Esempio
Trovare una soluzione approssimata a $\sin x = 0$ usando il metodo di Newton partendo da $x_1 = \frac{\pi}{2}$.
Soluzione
Impostiamo $f(x) = \sin x$, quindi $f'(x) = \cos x$. Ora $x_2$ = x_1 – \frac{f(x_1)}{f'(x_1)}$, ma $f'(x_1) = \cos \frac{\pi}{2} = 0$, quindi $x_2$ non è definito, e quindi nemmeno i successivi $x_n$.
Questo problema si presenta ogni volta che $f'(x_n) = 0$. Se $x_n$ è un punto stazionario di $f$, allora il metodo di Newton cerca di dividere per zero – e fallisce.
Il prossimo esempio illustra che anche quando le “soluzioni approssimate” $x_n$ esistono, possono non “approssimare” molto bene una soluzione.
Esempio
Approssimare una soluzione a $-x^3 + 4x^2 – 2x + 2 = 0$ usando il metodo di Newton da $x_1 = 0$.
Soluzione
Lascia che $f(x) = -x^3 + 4x^2 – 2x + 2$, quindi $f'(x) = -3x^2 + 8x – 2$. Partendo da $x_1 = 0$, abbiamo
\
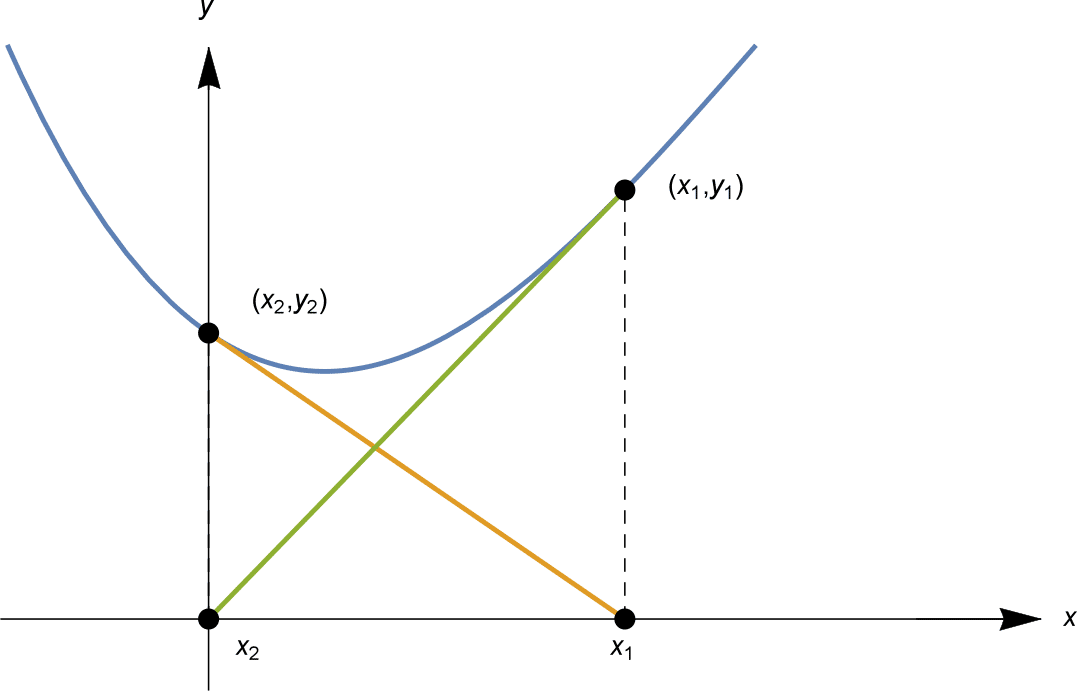
Ora abbiamo trovato che $x_3 = x_1 = 0$. Il calcolo per $x_4$ è quindi esattamente lo stesso di quello per $x_2$, quindi $x_4 = x_2 = 1$. Quindi $x_n = 0$ per tutti gli $n$ dispari, e $x_n = 1$ per tutti gli $n$ pari. Gli $x_n$ sono bloccati in un ciclo, alternando due valori.
Nell’esempio precedente, c’è effettivamente una soluzione, $x = \frac{1}{3} \sinistra( 4 + \sqrt{10} + \sqrt{100} \destra) \sim 3.59867$. Le nostre “soluzioni approssimate” $x_n$ non riescono ad approssimarla, invece pedalano come illustrato qui sotto.
Il terzo problema mostra che tutti $x_n$ possono allontanarsi sempre di più da una soluzione!
Esempio
Trova una soluzione approssimata a $\arctan x = 0$, usando il metodo di Newton partendo da $x_1 = 3$.
Soluzione
Lascia che $f(x) = \arctan x$, così $f'(x) = \frac{1}{1+x^2}$. Da $x_1 = 3$ possiamo calcolare successivamente $x_2, x_3, \ldots$. Li scriviamo con 2 cifre decimali.
\begin{align*}x_2 &= x_1 – \frac{f(x_1)}{f'(x_1)} = 3 – \frac{arctan 3}{frac{1}{1+3^2}} = 3 – 10 \arctan 3 \sim -9.49. \x_3 &= x_2 – \frac{f(x_2)}{f'(x_2)} \sim 124,00 \x_4 &= x_3 – \frac{f(x_3)}{f'(x_3)}
Le “approssimazioni” $x_n$ divergono rapidamente all’infinito.

L’esempio precedente può sembrare un po’ sciocco, poiché trovare una soluzione esatta a $\arctan x = 0$ non è difficile: la soluzione è $x=0$! Ma problemi simili accadranno applicando il metodo di Newton a qualsiasi curva con una forma simile. Il fatto che $f'(x_n)$ sia vicino a zero significa che la linea tangente è vicina all’orizzontale, e quindi può viaggiare molto lontano per arrivare alla sua intercetta $x$ di $x_{n+1}$.
Dipendenza sensibile dalle condizioni iniziali
A volte la scelta delle condizioni iniziali può essere minima, ma portare ad un risultato radicalmente diverso nel metodo di Newton.
Considera la soluzione di $f(x) = 2x – 3x^2 + x^3 = 0$. È possibile fattorizzare la cubica, $f(x) = x(x-1)(x-2)$, quindi le soluzioni sono solo $x=0, 1$ e $2$.
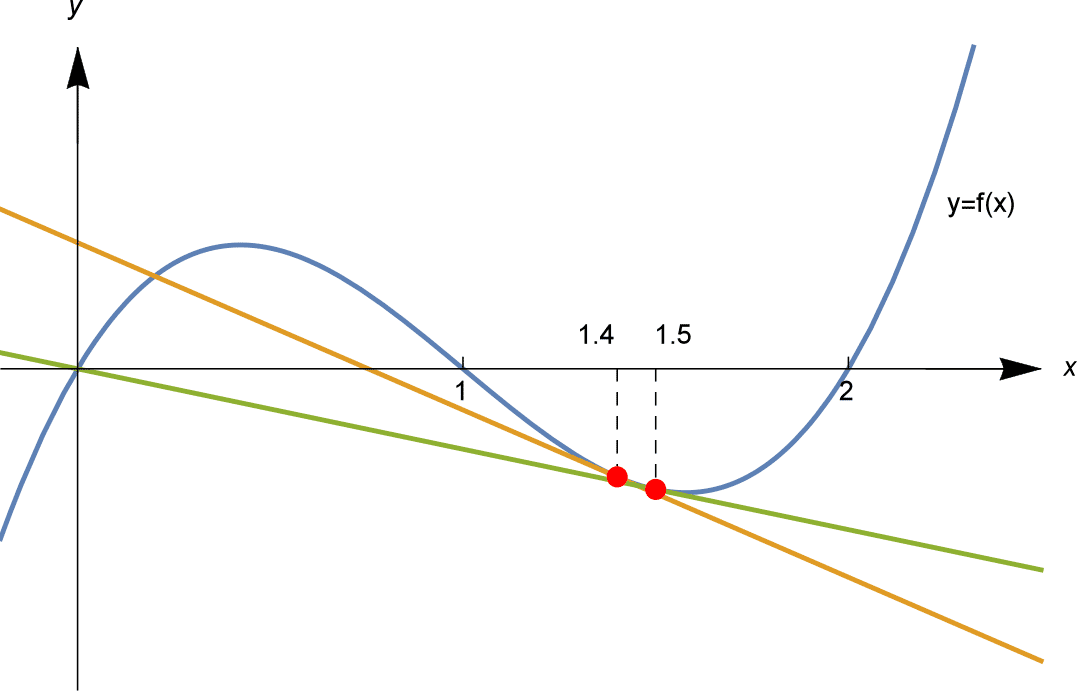
Se applichiamo il metodo di Newton con diverse stime di partenza $x_1$, potremmo finire in una di queste tre soluzioni…. o da qualche altra parte.
Come illustrato sopra, applichiamo il metodo di Newton partendo da $x_1 = 1,4$ e $x_1 = 1,5$. Partendo da $x_1 = 1,4 = \frac{7}{5}$ calcoliamo, con 6 cifre decimali,
e gli $x_n$ convergono alla soluzione $x=1$. E partendo da $x_1 = 1,5$ calcoliamo $x_2 = 0$, una soluzione esatta, per cui tutti $x_3 = x_4 = \cdots = 0$.
Possiamo allora chiederci: dove, tra le stime iniziali $x_1 = 1,4$ e $x_1 = 1.5$, la sequenza passa dall’avvicinarsi a $x=1$, all’avvicinarsi a $x=0$?
Troviamo che la stima iniziale $x_1 = 1,45$ si comporta in modo simile a $1,5$: la sequenza $x_n$ si avvicina alla soluzione $x = 0$. D’altra parte, prendere $x_1 = 1,44$ si comporta in modo simile a $1,4$: $x_n$ si avvicina alla soluzione $x=1$. Il risultato sembra passare da qualche parte tra le stime iniziali $x_1 = 1,44$ e $x_1 = 1,45$. Con qualche altro calcolo, possiamo restringere ulteriormente il campo e scoprire che il passaggio avviene da qualche parte tra $x_1 = 1,447$ e $x_1 = 1,448$. I calcoli (a 3 cifre decimali) da questi valori iniziali sono mostrati nella tabella qui sotto.
Quindi, se proviamo $x_1 = 1,4475$, gli $x_n$ convergeranno alla soluzione $x=1$ o $x=0$? La risposta è nessuna delle due: come mostrato nella tabella, converge alla soluzione $x=2$!
| $x_1$ | $1.4$ | $1.44$ | $1.447$ | $1.4475$ | $1.448$ | $1.45$ | $1.5$ | |
| $x_2$ | $0.754$ | $0.594$ | $0.554$ | $0.551$ | $0.548$ | 0,536$ | 0$ | |
| $x_3$ | $1,036$ | $1,266$ | $1,440$ | $1.458$ | $1.477$ | $1.567$ | $0$ | |
| $x_4$ | $1.000$ | $0.952$ | $0.596$ | $0.484$ | $0.317$ | $-9.156$ | $0$ | |
| $x_5$ | $1.000$ | $1.000$ | $1.260$ | $2.370$ | $-0.598$ | $-5.793$ | $0$ | |
| $x_6$ | $1.000$ | $1.000$ | $0.956$ | $2.111$ | $-0.225$ | $-3.562$ | $0$ | |
| $x_7$ | $1.000$ | $1.000$ | $1.000$ | $2.111$ | $-0.225$ | $-3.562$ | $0$ | |
| $x_8$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $-0.003$ | $-1.135$ | $0$ | |
| $x_9$ | $1.000$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.536$ | $0$ |
| $x_{10}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.192$ | $0$ | |
| $x_{11}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $0.038$ | $0$ | |
| $x_{12}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.002$ | $0$ |
Inoltre, se proviamo $x_1 = 1 + \frac{1}{sqrt{5}} \sim 1.447214$, troviamo di nuovo un comportamento diverso! Come si scopre,
così $x_1 = x_3$ e gli $x_n$ si alternano tra questi due valori.
Esercizio 12
Verifica che se $f(x) = 2x – 3x^2 + x^3 = x(x-1)(x-2)$ e $x_1 = 1 + \frac{1}{sqrt{5}}$, allora $x_2 = 1 – \frac{1}{sqrt{5}}$ e $x_3 = 1 + \frac{1}{sqrt{5}} = x_1$.
Quindi non c’è una semplice transizione tra i valori di $x_1$ che portano alla soluzione $x = 1$ e $x=0$. Il comportamento del metodo di Newton dipende in modo estremamente sensibile dall’iniziale $x_1$. Infatti, abbiamo provato solo una manciata di valori per $x_1$, e abbiamo visto solo la punta dell’iceberg di questo comportamento.
Nella sezione Link Forward esaminiamo ulteriormente questo comportamento, mostrando alcune immagini di questa sensibile dipendenza dalle condizioni iniziali, che è indicativa del caos matematico. Le immagini che illustrano il comportamento del metodo di Newton mostrano gli intricati dettagli di un frattale.
Far funzionare il metodo di Newton
In generale, è difficile affermare con precisione quando il metodo di Newton fornirà buone approssimazioni a una soluzione di $f(x) = 0$. Ma possiamo fare le seguenti note, riassumendo le nostre osservazioni precedenti.
- Se $f'(x_n) = 0$ allora il metodo di Newton fallisce immediatamente, poiché cerca di dividere per zero.
- Le “approssimazioni” $x_1, x_2, x_3, \ldots$ possono ciclare, piuttosto che convergere verso una soluzione.
- Le “soluzioni approssimate” $x_1, x_2, x_3, \ldots$ possono anche divergere all’infinito. Questo problema si verifica quando $f'(x_n)$ è piccolo, ma non nullo.
- Il comportamento del metodo di Newton può dipendere in modo estremamente sensibile dalla scelta di $x_1$, e portare a dinamiche caotiche.
Tuttavia, un’utile regola empirica è la seguente:
- Supponiamo di poter tracciare un grafico di $y=f(x)$, e di poter vedere la posizione approssimativa di una soluzione, e che $f'(x)$ non sia troppo piccola vicino a quella soluzione. Quindi prendendo $x_1$ vicino a quella soluzione, e lontano da altre soluzioni o punti critici, il metodo di Newton tenderà a produrre $x_n$ che convergono rapidamente alla soluzione.
Pagina successiva – Link in avanti – Velocità dell’algoritmo di bisezione
 |
Questi materiali sono stati sviluppati in collaborazione con la Victorian Curriculum and Assessment Authority. © VCAA e The University of Melbourne per conto di AMSI 2015 |
Collaboratori Termine di utilizzo |
th approssimazione $x_n$, l’approssimazione successiva è data da
Formalmente, l’algoritmo di Newton è il seguente.
Newton’s method
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable function. We seek a solution of $f(x) = 0$, starting from an initial estimate $x = x_1$.
At the $n$’th step, given $x_n$, compute the next approximation $x_{n+1}$ by
\
Some comments about this algorithm:
- Often, Newton’s method works extremely well, and the $x_n$ converge rapidly to a solution. However, it’s important to note that Newton’s method does not always work. Several things can go wrong, as we will see shortly.
- Note that if $f(x_n) = 0$, so that $x_n$ is an exact solution of $f(x) = 0$, then the algorithm gives $x_{n+1} = x_n$, and in fact all of $x_n, x_{n+1}, x_{n+2}, x_{n+3}, \ldots$ will be equal. If you have an exact solution, Newton’s method will stay on that solution!
- While the bisection method only requires $f$ to be continuous, Newton’s method requires the function $f$ to be differentiable. This is necessary for $f$ to have a tangent line.
Using Newton’s method
As we did with the bisection method, let’s approximate some well-known constants.
Example
Use Newton’s method to find an approximate solution to $x^2 – 2 = 0$, starting from an initial estimate $x_1 =2$. After 4 iterations, how close is the approximation to $\sqrt{2}$?
Solution
Let $f(x) = x^2 – 2$, so $f'(x) = 2x$. At step 1, we have $x_1 = 2$ and we calculate $f(x_1) = 2^2 – 2 = 2$ and $f'(x_1) = 4$, so
\
At step 2, from $x_2 = \frac{3}{2}$ we calculate $f(x_2) = \frac{1}{4}$ and $f'(x_2) = 3$, so
\
At step 3, from $x_3 = \frac{17}{12}$ we have $f(x_3) = \frac{1}{144}$ and $f'(x_3) = \frac{17}{6}$, so
\
At step 4, from $x_4 = \frac{577}{408}$ we calculate $f(x_4) = \frac{1}{166,464}$ and $f'(x_4) = \frac{577}{204}$, so
\
In fact, to 12 decimal places $\sqrt{2} \sim 1.414213562373$. So after 4 iterations, the approximate solution $x_5$ agrees with $\sqrt{2}$ to 11 decimal places. The difference between $x_5$ and $\sqrt{2}$ is
\
Newton’s method in the above example is much faster than the bisection algorithm! In only 4 iterations we have 11 decimal places of accuracy! The following table illustrates how many decimal places of accuracy we have in each $x_n$.
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
| # decimal places accuracy in | $0$ | $0$ | $2$ | $5$ | $11$ | $23$ | $47$ |
The number of decimal places of accuracy approximately doubles with each iteration!
Exercise 10
(Harder.) This problem investigates this doubling of accuracy:
- First calculate that $x_{n+1} = \frac{x_n}{2} + \frac{1}{x_n}$ and that, if $y_n = x_n – \sqrt{2}$, then $y_{n+1} = \frac{y_n^2}{2(\sqrt{2} + y_n)}$.
- Show that, if $x_1 > 0$ (resp. $x_1 \sqrt{2}$ (resp. $x_n
- Show that if $0
- Show that, for $n \geq 2$, if $x_n$ differs from $\sqrt{2}$ by less than $10^{-k}$, then $x_{n+1}$ differs from $\sqrt{2}$ by less than $10^{-2k}$.
Example
Find an approximation to $\pi$ by using Newton’s method to solve $\sin x = 0$ for 3 iterations, starting from $x_1=3$. To how many decimal places is the approximate solution accurate?
Solution
Let $f(x) = \sin x$, so $f'(x) = \cos x$. We compute $x_2, x_3, x_4$ directly using the formula
\
We compute directly each $x_n$ to 25 decimal places, for 3 iterations:
\
To 25 decimal places, $\pi = 3.1415926535897932384626433$; $x_4$ agrees to 24 places.
In the above example, convergence is even more rapid than for our $\sqrt{2}$ example. The number of decimal places accuracy roughly triples with each iteration!
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ |
| # decimal places accuracy in $x_n$ | $0$ | $2$ | $9$ | $24$ | $87$ |
Exercise 11
Find all solutions to the equation $\cos x = x$ to 9 decimal places using Newton’s method. Compare the convergence to what you obtained with the bisection method in exercise 5.
What can go wrong
While Newton’s method can give fantastically good approximations to a solution, several things can go wrong. We now examine some of this less fortunate behaviour.
The first problem is that the $x_n$ may not even be defined!
Example
Find an approximate solution to $\sin x = 0$ using Newton’s method starting from $x_1 = \frac{\pi}{2}$.
Solution
We set $f(x) = \sin x$, so $f'(x) = \cos x$. Now $x_2 = x_1 – \frac{f(x_1)}{f'(x_1)}$, but $f'(x_1) = \cos \frac{\pi}{2} = 0$, so $x_2$ is not defined, hence nor are any subsequent $x_n$.
This problem occurs whenever when $f'(x_n) = 0$. If $x_n$ is a stationary point of $f$, then Newton’s method attempts to divide by zero — and fails.
The next example illustrates that even when the “approximate solutions” $x_n$ exist, they may not “approximate” a solution very well.
Example
Approximate a solution to $-x^3 + 4x^2 – 2x + 2 = 0$ using Newton’s method from $x_1 = 0$.
Solution
Let $f(x) = -x^3 + 4x^2 – 2x + 2$, so $f'(x) = -3x^2 + 8x – 2$. Starting from $x_1 = 0$, we have
\
We have now found that $x_3 = x_1 = 0$. The computation for $x_4$ is then exactly the same as for $x_2$, so $x_4 = x_2 = 1$. Thus $x_n = 0$ for all odd $n$, and $x_n = 1$ for all even $n$. The $x_n$ are locked into a cycle, alternating between two values.
In the above example, there is actually a solution, $x = \frac{1}{3} \left( 4 + \sqrt{10} + \sqrt{100} \right) \sim 3.59867$. Our “approximate solutions” $x_n$ fail to approximate it, instead cycling as illustrated below.

The third problem shows that all $x_n$ can get further and further away from a solution!
Example
Find an approximate solution to $\arctan x = 0$, using Newton’s method starting at $x_1 = 3$.
Solution
Let $f(x) = \arctan x$, so $f'(x) = \frac{1}{1+x^2}$. From $x_1 = 3$ we can compute successively $x_2, x_3, \ldots$. We write them to 2 decimal places.
\begin{align*}x_2 &= x_1 – \frac{f(x_1)}{f'(x_1)} = 3 – \frac{\arctan 3}{\frac{1}{1+3^2}} = 3 – 10 \arctan 3 \sim -9.49. \\x_3 &= x_2 – \frac{f(x_2)}{f'(x_2)} \sim 124.00 \\x_4 &= x_3 – \frac{f(x_3)}{f'(x_3)} \sim -23,905.94\end{align*}
The “approximations” $x_n$ rapidly diverge to infinity.

The above example may seem a little silly, since finding an exact solution to $\arctan x = 0$ is not difficult: the solution is $x=0$! But similar problems will happen applying Newton’s method to any curve with a similar shape. The fact that $f'(x_n)$ is close to zero means the tangent line is close to horizontal, and so may travel far away to arrive at its $x$-intercept of $x_{n+1}$.
Sensitive dependence on initial conditions
Sometimes the choice of initial conditions can be ever so slight, yet lead to a radically different outcome in Newton’s method.
Consider solving $f(x) = 2x – 3x^2 + x^3 = 0$. It’s possible to factorise the cubic, $f(x) = x(x-1)(x-2)$, so the solutions are just $x=0, 1$ and $2$.

If we apply Newton’s method with different starting estimates $x_1$, we might end up at any of these three solutions… or somewhere else.
As illustrated above, we apply Newton’s method starting from $x_1 = 1.4$ and $x_1 = 1.5$. Starting from $x_1 = 1.4 = \frac{7}{5}$ we compute, to 6 decimal places,
\
and the $x_n$ converge to the solution $x=1$. And starting from $x_1 = 1.5$ we compute $x_2 = 0$, an exact solution, so all $x_3 = x_4 = \cdots = 0$.
We might then ask: where, between the initial estimates $x_1 = 1.4$ and $x_1 = 1.5$, does the sequence switch from approaching $x=1$, to approaching $x=0$?
We find that the the initial estimate $x_1 = 1.45$ behaves similarly to $1.5$: the sequence $x_n$ approaches the solution $x = 0$. On the other hand, taking $x_1 = 1.44$ behaves similarly to $1.4$: $x_n$ approaches the solution $x=1$. The outcome seems to switch somewhere between the initial estimates $x_1 = 1.44$ and $x_1 = 1.45$. With some more computations, we can narrow down further and find that the switch happens somewhere between $x_1 = 1.447$ and $x_1 = 1.448$. The computations (to 3 decimal places) from these initial values are shown in the table below.
So, if we try $x_1 = 1.4475$, will the $x_n$ converge to the solution $x=1$ or $x=0$? The answer is neither: as shown in the table, it converges to the solution $x=2$!
| $x_1$ | $1.4$ | $1.44$ | $1.447$ | $1.4475$ | $1.448$ | $1.45$ | $1.5$ |
| $x_2$ | $0.754$ | $0.594$ | $0.554$ | $0.551$ | $0.548$ | $0.536$ | $0$ |
| $x_3$ | $1.036$ | $1.266$ | $1.440$ | $1.458$ | $1.477$ | $1.567$ | $0$ |
| $x_4$ | $1.000$ | $0.952$ | $0.596$ | $0.484$ | $0.317$ | $-9.156$ | $0$ |
| $x_5$ | $1.000$ | $1.000$ | $1.260$ | $2.370$ | $-0.598$ | $-5.793$ | $0$ |
| $x_6$ | $1.000$ | $1.000$ | $0.956$ | $2.111$ | $-0.225$ | $-3.562$ | $0$ |
| $x_7$ | $1.000$ | $1.000$ | $1.000$ | $2.111$ | $-0.225$ | $-3.562$ | $0$ |
| $x_8$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $-0.003$ | $-1.135$ | $0$ |
| $x_9$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.536$ | $0$ |
| $x_{10}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.192$ | $0$ |
| $x_{11}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.038$ | $0$ |
| $x_{12}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.002$ | $0$ |
Furthermore, if we try $x_1 = 1 + \frac{1}{\sqrt{5}} \sim 1.447214$, we find different behaviour again! As it turns out,
\
so $x_1 = x_3$ and the $x_n$ alternate between these two values.
Exercise 12
Verify that if $f(x) = 2x – 3x^2 + x^3 = x(x-1)(x-2)$ and $x_1 = 1 + \frac{1}{\sqrt{5}}$, then $x_2 = 1 – \frac{1}{\sqrt{5}}$ and $x_3 = 1 + \frac{1}{\sqrt{5}} = x_1$.
So there is no simple transition from those values of $x_1$ which lead to the solution $x = 1$ and $x=0$. The behaviour of Newton’s method depends extremely sensitively on the initial $x_1$. Indeed, we have only tried only a handful of values for $x_1$, and have only seen the tip of the iceberg of this behaviour.
In the Links Forward section we examine this behaviour further, showing some pictures of this sensitive dependence on initial conditions, which is indicative of mathematical chaos. Pictures illustrating the behaviour of Newton’s method show the intricate detail of a fractal.
Getting Newton’s method to work
In general, it is difficult to state precisely when Newton’s method will provide good approximations to a solution of $f(x) = 0$. But we can make the following notes, summarising our previous observations.
- If $f'(x_n) = 0$ then Newton’s method immediately fails, as it attempts to divide by zero.
- The “approximations” $x_1, x_2, x_3, \ldots$ can cycle, rather than converging to a solution.
- The “approximate solutions” $x_1, x_2, x_3, \ldots$ can even diverge to infinity. This problem happens when $f'(x_n)$ is small, but not zero.
- The behaviour of Newton’s method can depend extremely sensitively on the choice of $x_1$, and lead to chaotic dynamics.
However, a useful rule of thumb is as follows:
- Suppose you can sketch a graph of $y=f(x)$, and you can see the approximate location of a solution, and $f'(x)$ is not too small near that solution. Then taking $x_1$ near that solution, and away from other solutions or critical points, Newton’s method will tend to produce $x_n$ which converge rapidly to the solution.
Next page – Links forward – Speed of the bisection algorithm
 |
These materials have been developed in collaboration with the Victorian Curriculum and Assessment Authority. © VCAA and The University of Melbourne on behalf of AMSI 2015 |
Contributors Term of use |