Abbiamo definito che la funzione logaritmica y = log b x è la funzione inversa della funzione esponenziale y = b x. Possiamo ora procedere al grafico di funzioni logaritmiche guardando la relazione tra funzioni esponenziali e logaritmiche.
Ma prima di saltare nell’argomento del grafico delle funzioni logaritmiche, è importante familiarizzare con i seguenti termini:
- Il dominio di una funzione
Il dominio di una funzione è un insieme di valori che si possono sostituire nella funzione per ottenere una risposta accettabile.
- L’intervallo di una funzione
Questo è l’insieme di valori che si ottiene dopo aver sostituito i valori nel dominio per la variabile.
- Asintoti
Ci sono tre tipi di asintoti, cioè: verticale, orizzontale e obliquo. L’asintoto verticale è il valore di x dove la funzione cresce senza limiti nelle vicinanze.
Gli asintoti orizzontali sono valori costanti a cui f(x) si avvicina al crescere di x senza limiti. Gli asintoti obliqui sono polinomi di primo grado a cui f(x) si avvicina man mano che x cresce senza limiti.
Come rappresentare graficamente le funzioni logaritmiche?
Il grafico di una funzione logaritmica può essere fatto esaminando il grafico della funzione esponenziale e poi scambiando x e y.
Il grafico di una funzione esponenziale f (x) = b x o y = b x contiene le seguenti caratteristiche:
- Il dominio di una funzione esponenziale è costituito da numeri reali (-infinito, infinito).
- Anche l’intervallo è costituito da numeri reali positivi (0, infinito)
- Il grafico di una funzione esponenziale passa normalmente per il punto (0, 1). Questo significa che la y – intercetta è nel punto (0, 1).
- Il grafico di una funzione esponenziale f(x) = b x ha un asintoto orizzontale in y = 0.
- Un grafico esponenziale diminuisce da sinistra a destra se 0 < b < 1, e questo caso è noto come decadimento esponenziale.
- Se la base della funzione f(x) = b x è maggiore di 1, allora il suo grafico aumenterà da sinistra a destra e si chiama crescita esponenziale.
Guardando le caratteristiche di cui sopra una alla volta, possiamo analogamente dedurre le caratteristiche delle funzioni logaritmiche come segue:
- Una funzione logaritmica avrà come dominio (0, infinito).
- L’intervallo di una funzione logaritmica è (-infinito, infinito).
- Il grafico della funzione logaritmica passa per il punto (1, 0), che è l’inverso di (0, 1) per una funzione esponenziale.
- Il grafico di una funzione logaritmica ha un asintoto verticale in x = 0.
- Il grafico di una funzione logaritmica diminuisce da sinistra a destra se 0 < b < 1.
- E se la base della funzione è maggiore di 1, b > 1, allora il grafico aumenterà da sinistra a destra.
Una funzione logaritmica di base è generalmente una funzione senza spostamento orizzontale o verticale.
Questi sono i passi per creare un grafico di una funzione logaritmica di base.
- Siccome tutte le funzioni logaritmiche passano per il punto (1, 0), individuiamo e mettiamo un punto nel punto.
- Per evitare che la curva tocchi l’asse y, disegniamo un asintoto in x = 0.
- Se la base della funzione è maggiore di 1, aumentate la vostra curva da sinistra a destra. Allo stesso modo, se la base è minore di 1, diminuisci la curva da sinistra a destra.
Ora guardiamo i seguenti esempi:
Esempio 1
Registra la funzione logaritmica f(x) = log 2 x e dichiara l’intervallo e il dominio della funzione.
Soluzione
- Ovviamente, una funzione logaritmica deve avere il dominio e l’intervallo di (0, infinito) e (-infinito, infinito)
- Siccome la funzione f(x) = log 2 x è maggiore di 1, aumenteremo la nostra curva da sinistra a destra, come mostrato sotto.
- Non possiamo vedere l’asintoto verticale a x = 0 perché è nascosto dall’asse y.
Esempio 2
Disegna un grafico di y = log 0.5 x
Soluzione
- Posiziona un punto nel punto (1, 0). Tutte le curve logaritmiche passano per questo punto.
- Disegna un asintoto in x = 0.
- Siccome la base della funzione y = log 5 x è minore di 1, diminuiremo la nostra curva da sinistra a destra.
- La funzione y = log 5 x avrà anche (0, infinito) e (-infinito, infinito) come dominio e intervallo.
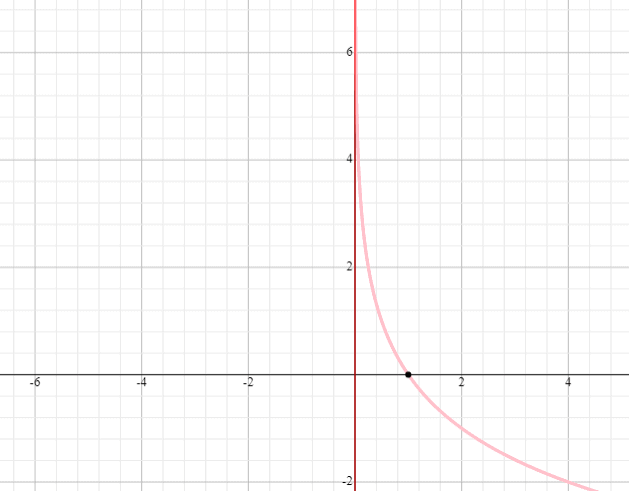
Grafico di una funzione logaritmica con spostamento orizzontale
Le funzioni logaritmiche con spostamento orizzontale sono della forma f(x) = log b (x + h) o f (x) = log b (x – h), dove h = lo spostamento orizzontale. Il segno dello spostamento orizzontale determina la direzione dello spostamento. Se il segno è positivo, lo spostamento sarà negativo, e se il segno è negativo, lo spostamento diventa positivo.
Applicando lo spostamento orizzontale, le caratteristiche di una funzione logaritmica sono influenzate nei seguenti modi:
- La x – intercetta si sposta a sinistra o a destra di una distanza fissa pari a h.
- L’asintoto verticale si sposta di una distanza uguale a h.
- Anche il dominio della funzione cambia.
Esempio 3
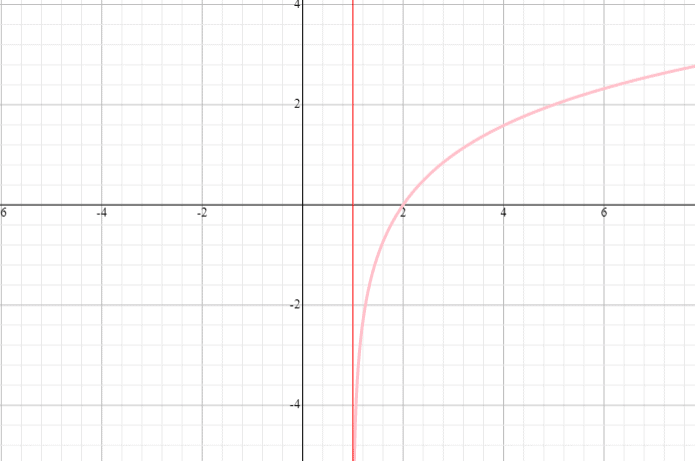
Disegna un grafico della funzione f(x) = log 2 (x + 1) e indica il dominio e l’intervallo della funzione.
Soluzione
⟹ Dominio: (- 1, infinito)
⟹ Campo: (-infinito, infinito)
Esempio 4
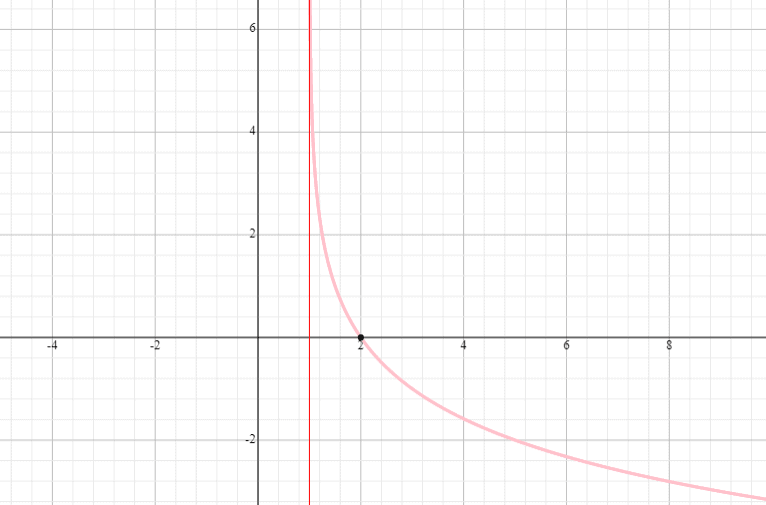
Grafico y = log 0.5 (x – 1) e indicare il dominio e l’intervallo.
Soluzione
⟹ Dominio: (1, infinito)
⟹ Intervallo: (-infinito, infinito)
Come rappresentare una funzione con una verticale?
Una funzione logaritmica con spostamento sia orizzontale che verticale è della forma f(x) = log b (x) + k, dove k = lo spostamento verticale.
Lo spostamento verticale influenza le caratteristiche di una funzione come segue:
- L’intercetta x si sposterà verso l’alto o verso il basso con una distanza fissa di k
Esempio 5
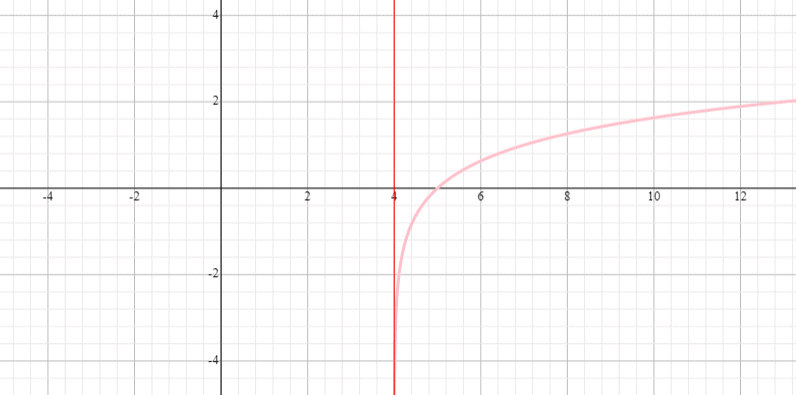
Grafica la funzione y = log 3 (x – 4) e indica l’intervallo e il dominio della funzione.
Soluzione
⟹ Dominio: (0, infinito)
⟹ Intervallo: (-infinito, infinito)
Funzioni con spostamento orizzontale e verticale
Una funzione logaritmica con spostamento orizzontale e verticale è della forma (x) = log b (x + h) + k, dove k e h sono rispettivamente gli spostamenti verticale e orizzontale.
Esempio 6
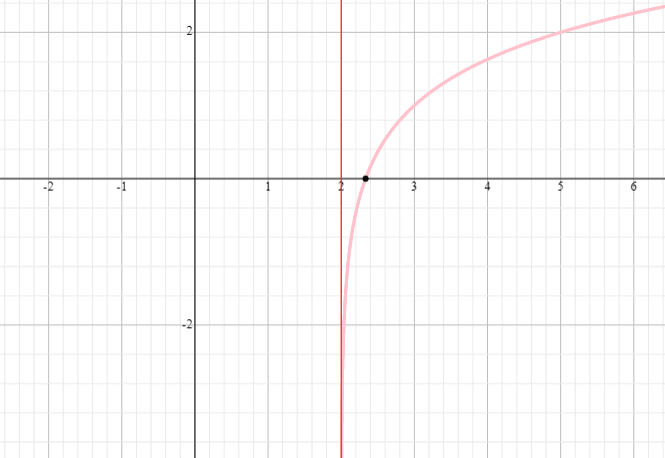
Registra la funzione logaritmica y = log 3 (x – 2) + 1 e trova il dominio e l’intervallo della funzione.
Soluzione
⟹ Dominio: (2,infinito)
⟹ Intervallo: (-infinito, infinito)
Esempio 7
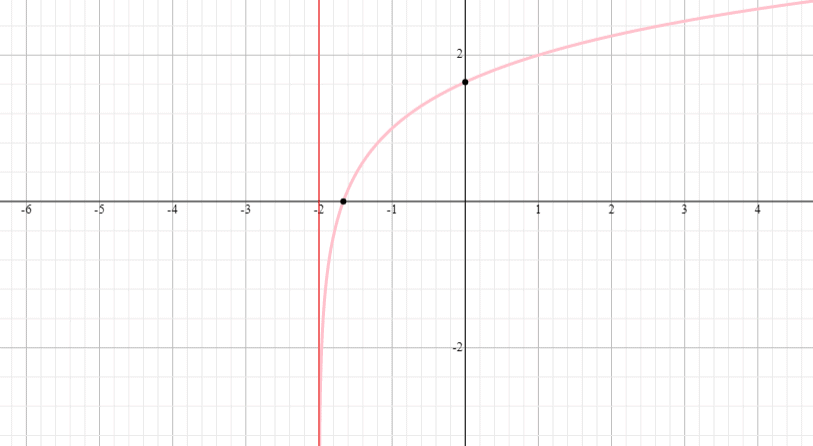
Grafica la funzione logaritmica y = log 3 (x + 2) + 1 e trova il dominio e l’intervallo della funzione.
Soluzione
⟹ Dominio: (- 2,infinito)
⟹ Intervallo: (-infinito, infinito)
Lezione precedente | Pagina principale | Lezione successiva