Regressione Probit
Nella regressione Probit, la funzione di distribuzione normale standard cumulativa \(\Phi(\cdot)\) è usata per modellare la funzione di regressione quando la variabile dipendente è binaria, cioè si assume
(\beta_0 + \beta_1 X\) in (11.4) gioca il ruolo di un quantile \(z\). Ricorda che \ tale che il coefficiente Probit \(\beta_1\) in (11.4) è il cambiamento di \(z\) associato ad un cambiamento di una unità in \(X\). Sebbene l’effetto su \(z) di una variazione di \(X) sia lineare, il legame tra \(z) e la variabile dipendente \(Y) è non lineare poiché \(\Phi\) è una funzione non lineare di \(X).
Siccome la variabile dipendente è una funzione non lineare dei regressori, il coefficiente su \(X) non ha una semplice interpretazione. Secondo il Concetto Chiave 8.1, il cambiamento atteso nella probabilità che \(Y=1\) dovuto a un cambiamento di \(P/I \ rapporto) può essere calcolato come segue:
- Computa la probabilità prevista che \(Y=1\) per il valore originale di \(X\).
- Computa la probabilità prevista che \(Y=1\) per \(X + \Delta X\).
- Computa la differenza tra le due probabilità previste.
Naturalmente possiamo generalizzare (11.4) alla regressione Probit con regressori multipli per mitigare il rischio di incorrere in errori di variabili omesse. Gli elementi essenziali della regressione Probit sono riassunti nel concetto chiave 11.2.
Modello Probit, probabilità previste ed effetti stimati
Assumiamo che \(Y\) sia una variabile binaria. Il modello
è il modello Probit della popolazione con regressori multipli \(X_1, X_2, \punti, X_k\) e \(\Phi(\cdot)\) è la funzione di distribuzione standard cumulativa.
La probabilità prevista che \(Y=1\) dato \(X_1, X_2, \punti, X_k\) può essere calcolata in due passi:
-
Computa \(z = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \punti + \beta_k X_k\)
-
Cerca \(\Phi(z)\) chiamando pnorm().
(\beta_j\) è l’effetto su \(z\) di un cambiamento di una unità nel regressore \(X_j\), mantenendo costanti tutti gli altri \(k-1\) regressori.
L’effetto sulla probabilità prevista di un cambiamento in un regressore può essere calcolato come nel concetto chiave 8.1.
In R, i modelli Probit possono essere stimati usando la funzione glm() dal pacchetto stats. Usando l’argomento family specifichiamo che vogliamo usare una funzione di collegamento Probit.
Stimiamo ora un semplice modello Probit della probabilità di rifiuto di un mutuo.
# estimate the simple probit modeldenyprobit <- glm(deny ~ pirat, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Il modello stimato è
Proprio come nel modello di probabilità lineare troviamo che la relazione tra la probabilità di rifiuto e il rapporto pagamenti/reddito è positiva e che il coefficiente corrispondente è altamente significativo.
Il seguente codice riproduce la figura 11.2 del libro.
# plot dataplot(x = HMDA$pirat, y = HMDA$deny, main = "Probit Model of the Probability of Denial, Given P/I Ratio", xlab = "P/I ratio", ylab = "Deny", pch = 20, ylim = c(-0.4, 1.4), cex.main = 0.85)# add horizontal dashed lines and textabline(h = 1, lty = 2, col = "darkred")abline(h = 0, lty = 2, col = "darkred")text(2.5, 0.9, cex = 0.8, "Mortgage denied")text(2.5, -0.1, cex= 0.8, "Mortgage approved")# add estimated regression linex <- seq(0, 3, 0.01)y <- predict(denyprobit, list(pirat = x), type = "response")lines(x, y, lwd = 1.5, col = "steelblue")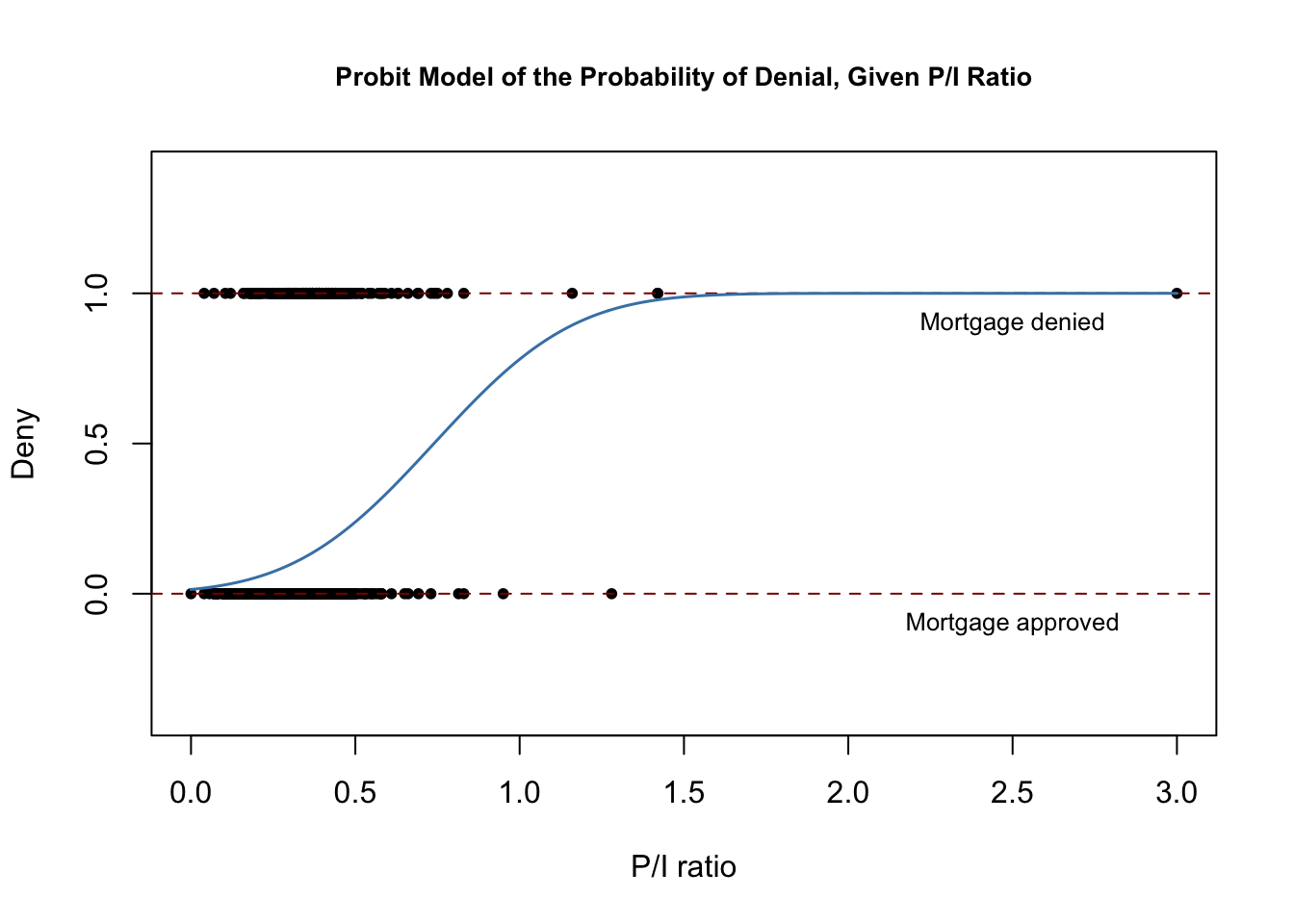
La funzione di regressione stimata ha una forma a “S” allungata che è tipica della CDF di una variabile casuale continua con PDF simmetrica come quella di una variabile casuale normale. La funzione è chiaramente non lineare e si appiattisce per valori grandi e piccoli del rapporto \(P/I \). La forma funzionale assicura quindi anche che le probabilità condizionali previste di un rifiuto siano comprese tra \(0\) e \(1\).
Utilizziamo predict() per calcolare il cambiamento previsto nella probabilità di rifiuto quando \(P/I rapporto \) viene aumentato da \(0..3\) a \0.4\).
# 1. compute predictions for P/I ratio = 0.3, 0.4predictions <- predict(denyprobit, newdata = data.frame("pirat" = c(0.3, 0.4)), type = "response")# 2. Compute difference in probabilitiesdiff(predictions)#> 2 #> 0.06081433Troviamo che un aumento del rapporto pagamento/reddito da \(0.3\) a \(0.4\) è previsto per aumentare la probabilità di rifiuto di circa \(6..
Continuiamo usando un modello Probit aumentato per stimare l’effetto della razza sulla probabilità di rifiuto di una richiesta di mutuo.
denyprobit2 <- glm(deny ~ pirat + black, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1L’equazione stimata del modello è
Mentre tutti i coefficienti sono altamente significativi, sia i coefficienti stimati sul rapporto pagamenti/reddito che l’indicatore di discendenza afroamericana sono positivi. Di nuovo, i coefficienti sono difficili da interpretare, ma indicano che, in primo luogo, gli afroamericani hanno una maggiore probabilità di rifiuto rispetto ai richiedenti bianchi, mantenendo costante il rapporto pagamenti/reddito e in secondo luogo, i richiedenti con un alto rapporto pagamenti/reddito affrontano un rischio maggiore di essere respinti.
Quanto è grande la differenza stimata nelle probabilità di rifiuto tra due ipotetici richiedenti con lo stesso rapporto pagamenti/reddito? Come prima, possiamo usare predict() per calcolare questa differenza.
# 1. compute predictions for P/I ratio = 0.3predictions <- predict(denyprobit2, newdata = data.frame("black" = c("no", "yes"), "pirat" = c(0.3, 0.3)), type = "response")# 2. compute difference in probabilitiesdiff(predictions)#> 2 #> 0.1578117In questo caso, la differenza stimata nelle probabilità di rifiuto è circa \(15.8\%\).