Calcolo dell’impedenza
Nei circuiti AC, la legge di Ohm assume la forma più generale: E = I⋅Z, dove E è la tensione e I è la corrente, come prima. Il nuovo termine, Z, è l’impedenza, una combinazione vettoriale di:
- Resistenza, R (in ohm), con cadute di tensione in fase con la corrente.
- Reattanza induttiva, XL (in ohm), con cadute di tensione che precedono la corrente di 90°.
- Reattanza capacitiva, XC (in ohm) con le gocce di tensione che seguono la corrente di 90°.
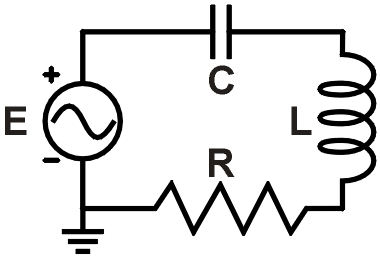
f = 6,4 kHz R = 120 Ω
L = 3,6 mH C = 0,38 μf
Figura 1. Esempio di circuito RLC

Figura 2. La somma vettoriale di R e
XL-XC produce Z
Dalle formule per XL e XC, si può vedere che le reattanze dipendono sia dai valori dei componenti L e C, sia dalla frequenza AC, f:
![]() e
e 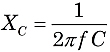
dove f è la frequenza inHertz (o sec-1), L è l’induttanza in Henries, e C è la capacità in farad. Poiché XL e XCare sono 180° diversi in fase, la reattanza totale X di un circuito in serie è XL-XC.
Gli usi familiari della legge di Ohm, come i calcoli dei circuiti in serie e in parallelo, si applicano ancora. Tuttavia, si devono ora considerare i contributi vettoriali concorrenti di resistenze e reattanze.
Angoli di fase e vettori
Troviamo l’impedenza totale del circuito in figura 1. Usando le formule precedenti:
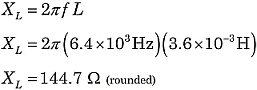 |
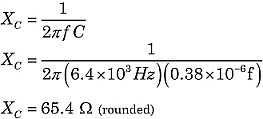 |
Costruendo l’impedenza Z, la resistenza contribuisce alla componente orizzontale. La componente verticale è la differenza delle reattanze: Quindi, Z è la somma vettoriale di R e XL-XC, come illustrato nella figura 2.
Nella figura 2, visto che Z è l’ipotenusa di un triangolo rettangolo, possiamo usare il teorema di Pitagora e la geometria del triangolo rettangolo per valutare Z.
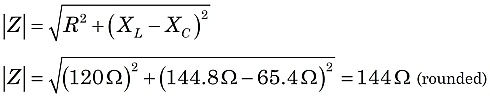
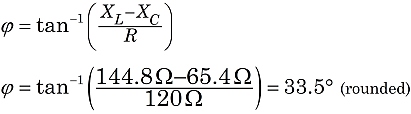
Quindi, in questo circuito, assisteremmo all’effetto di un’impedenza di144 ohm, con la corrente in ritardo rispetto alla tensione di alimentazione con un angolo di fase di 33.5°.
Come si può intuire dalla discussione precedente, è abbastanza possibile che le reattanze induttive e capacitive si annullino esattamente sotto la giusta combinazione di valori L, C e f. Questa è una condizione molto importante conosciuta come risonanza.