Em aplicações de engenharia, encontramos frequentemente funções cujos valores mudam abruptamente a valores especificados de tempo t. Um exemplo comum é quando uma tensão é ligada ou desligada num circuito eléctrico a um valor especificado de tempo t.
Later, nesta página…
Função de passo de unidade deslocada
P>Pulso retangular
O valor de t = 0 é normalmente tomado como um tempo conveniente para ligar ou desligar a tensão dada.
O processo de comutação pode ser descrito matematicamente pela função chamada Função Passo de Unidade (também conhecida como função Heaviside depois de Oliver Heaviside).
A Função Passo de Unidade
Definição: A função de passo unitário, `u(t)`, é definida como
`u(t)={: {(0, t < 0), (1, t > 0) :}`
Isto é, u é uma função do tempo t, e u tem valor zero quando o tempo é negativo (antes de virarmos o interruptor); e valor um quando o tempo é positivo (de quando virarmos o interruptor).
Gráfico de `f(t)=u(t)`, a função de passo da unidade.
Valor em t = 0?
Em alguns livros de texto verá a função de passo da unidade definida como tendo valor 1 em t = 0, como se segue:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
Indicamos a descontinuidade no nosso gráfico desta forma:
Gráfico de `f(t)=u(t)`, a função de passo da unidade, com `f(0) = 1`.
Também, por vezes veremos o valor dado como `f(0) = 0.5`.
Neste trabalho, não faz grande diferença nos nossos cálculos, pelo que continuaremos a utilizar a primeira interpretação, e a desenhar os nossos gráficos em conformidade.
Função de passo de unidade deslocada
Em muitos circuitos, as formas de onda são aplicadas a intervalos especificados que não `t=0`. Tal função pode ser descrita utilizando a função de passo de unidade deslocada (aka atrasada).
Definição da função de passo de unidade deslocada
É escrita uma função que tem o valor `0` até ao tempo `t = a` e, posteriormente, tem o valor `1`:
`u(t-a)={{: (0, if, t < a), (1, if, t > a) :}`
Exemplo 1 – Função do Passo da Unidade Deslocada
`f(t) = u(t – 3)`
The equação significa f(t) tem o valor de `0` quando `t < 3` e `1` quando `t > 3`.
O esboço da forma de onda é o seguinte:
Gráfico de `f(t)=u(t-3)`, uma função de passo de unidade deslocada.
Pulso rectangular
Uma situação comum num circuito é que uma tensão seja aplicada num determinado momento (digamos t = a) e removida mais tarde, em t = b (digamos). Escrevemos tal situação utilizando funções de passos de unidade como:
`V(t) = u(t – a) – u(t – b)`
Esta tensão tem força `1`, duração `(b – a)`.
Exemplo 2 – Pulso rectangular
O gráfico de `V(t) = u(t – 1.2) – u(t – 3.8)` é o seguinte. Aqui, a duração é `3.8 – 1.2 = 2.6`.
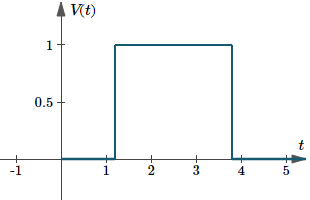
Gráfico de `V(t)=u(t-1.2)-u(t-3.8)-u(t-3.8)`, um exemplo de um impulso rectangular.
Exercícios
Papel gráfico de alimentação?
Escrever as seguintes funções em termos de função(ões) do passo da unidade. Esboçar cada forma de onda.
(a) Uma fonte 12-V é ligada a t = 4 s.
Resposta
p>Desde que a tensão é ligada a t = 4, precisamos de usar u(t – 4). Multiplicamos por 12, uma vez que é essa a voltagem.
Escrevemos a função da seguinte forma:
`V(t)=12-u(t-4)`.
Aqui está o gráfico:
Gráfico de `V(t)=12-u(t-4)`, uma função de passo deslocado.
(b) `V(t)={{: (1, 0 < t < a),(0, t > a) :}“
(Assumir a > 0.)
Resposta
Em palavras, a voltagem tem valor `1` até ao tempo `t = a`. Depois é desligada.
Temos uma situação de “pulso rectangular” e precisamos de utilizar esta fórmula:
`V(t) = u(t – a) – u(t – b)`
No nosso exemplo, o impulso começa em `t = 0`, por isso utilizamos `u(t)`, e termina em `t = a`, por isso utilizamos `u(t – a)`.
Assim, a função requerida é:
`V(t)=1-` `=u(t)-u(t-a)`
Gráfico de `V(t)=u(t)-u(t-a)`, uma função de passo de unidade deslocada.
(c) Um ciclo de uma onda quadrada, `f(0) = 4`, amplitude = “4`, período = “2` segundos.
Resposta
`f(0) = 4` significa que começamos no valor `4`.
Se toda a onda tem o período `2`, e é uma onda quadrada, então significa para metade do tempo, o valor é (positivo) `4` e a outra metade é `-4`.
Então para o primeiro segundo, tem o valor `4`, para o segundo, o valor da função é `-4`.
Escrevemos isto, utilizando a fórmula “pulso rectangular” de antes:
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
O gráfico deste primeiro ciclo é:
Gráfico de `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, uma onda quadrada.
(d) A unidade Função Rampa (isto é`f(t) = t` for `t > 0`)
Resposta
A função de rampa da unidade tem inclinação `1` , começando por `t = 0` , e passa por `(0, 0)`.
Assim a função de voltagem é dada por:
`V(t) = t – u(t)`
O gráfico da função é:
Gráfico de `V(t)=t – u(t)`, a função de rampa da unidade.
(e) Um ciclo de uma forma de onda de dente de serra (i.e. `f(t)=a/b t` for `0 < t < b`. Assumir `a > 0`.)
Resposta
O nosso gráfico começa em `t = 0` e tem inclinação `a / b`. Acaba em `t = b`.
Por isso a nossa função será:
`f(t)=a/b t – {u(t)-u(t-b)}`
O gráfico da nossa função:
Gráfico de `f(t)=a/b t – {u(t)-u(t-b)}`, uma forma de onda de dente de serra.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t 5) :}`
Resposta
Neste exemplo, a nossa função é `V(t) = 2t + 8` que tem inclinação `2` e `V`-intercepção `8`.
O sinal só é ligado entre `t = 3` e `t = 5`. O resto do tempo está desligado.
Por isso, a nossa função de voltagem será:
“V(t) ` `= (2t+8) -{u(t – 3)- u(t – 5)}`
O gráfico é o seguinte:
Gráfico de `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}“. A linha tracejada é `V(t) = (2t + 8`.
top
Procura IntMath
Solvente de cálculo em linha
Este solver de cálculo pode resolver uma vasta gama de problemas matemáticos.
Vai para: Solver calculus online