Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Définir les surfaces équipotentielles et les lignes équipotentielles
- Expliquer la relation entre les lignes équipotentielles et les lignes de champ électrique
- Mapper les lignes équipotentielles pour une ou deux charges ponctuelles
- Décrire le potentiel d’un conducteur
- Comparer et opposer les lignes équipotentielles et les lignes d’élévation sur les cartes topographiques
.
Nous pouvons représenter les potentiels électriques (tensions) de manière imagée,tout comme nous avons dessiné des images pour illustrer les champs électriques. Cela n’est pas surprenant, puisque les deux concepts sont liés. Considérez la figure\(\PageIndex{1}\), qui montre une charge ponctuelle positive isolée et ses lignes de champ électrique, qui rayonnent à partir d’une charge positive et se terminent sur des charges négatives. Nous utilisons des flèches bleues pour représenter l’amplitude et la direction du champ électrique, et des lignes vertes pour représenter les endroits où le potentiel électrique est constant. Ces surfaces sont appelées surfaces équipotentielles en trois dimensions, ou lignes équipotentielles en deux dimensions. Le terme équipotentiel est également utilisé comme substantif pour désigner une ligne ou une surface équipotentielle. Le potentiel d’une charge ponctuelle est le même partout sur une sphère imaginaire de rayon r entourant la charge. Ceci est vrai car le potentiel d’une charge ponctuelle est donné par \(V = kq/r\) et a donc la même valeur en tout point situé à une distance donnée de la charge. Une sphère équipotentielle est un cercle dans la vue bidimensionnelle de la figure \(\PageIndex{1}\). Les lignes de champ électrique étant radialement éloignées de la charge, elles sont perpendiculaires aux lignes équipotentielles.
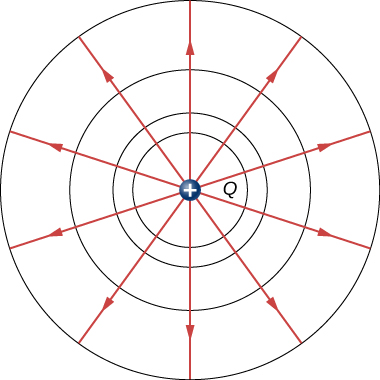
Il est important de noter que les lignes équipotentielles sont toujoursperpendiculaires aux lignes de champ électrique. Aucun travail n’est nécessaire pour déplacer une charge le long d’une équipotentielle, puisque \(\Delta V = 0\). Ainsi, le travail est
Le travail est nul si la direction de la force est perpendiculaire au déplacement. La force est dans la même direction que \(E\), un déplacement le long d’une équipotentielle doit être perpendiculaire à \(E\). Plus précisément, le travail est lié au champ électrique par
\ &= q\vec{E} \cdot \vec{d} &= qEd\, \cos \, \theta \nonumber \\\\N &= 0. \nonumber \end{align}\nonumber\]
Notez que dans l’équation \ref{eq5}, \(E\) et \(F\) symbolisent les magnitudes du champ électrique et de la force, respectivement. Ni \(q\) ni \(E\) ne sont nuls et \(d\) ne l’est pas non plus. Donc \(\cos \,\theta\) doit être 0, ce qui signifie que \(\theta\) doit être \(90^o\). En d’autres termes, le mouvement le long d’une équipotentielle est perpendiculaire àE.
L’une des règles concernant les champs électriques statiques et les conducteurs est que le champ électrique doit être perpendiculaire à la surface de toutconducteur. Cela implique qu’un conducteur est une surface équipotentielle en situation statique. Il ne peut y avoir de différence de tension à la surface d’un conducteur, sinon des charges circuleront.L’une des utilisations de ce fait est qu’un conducteur peut être fixé à ce que nous considérons comme zéro volt en le reliant à la terre avec un bon conducteur – un processus appelé mise à la terre. La mise à la terre peut être un outil de sécurité utile. Par exemple, la mise à la terre du boîtier métallique d’un appareil électrique permet de s’assurer qu’il est à zéro volt par rapport à la Terre.
Parce qu’un conducteur est un équipotentiel, il peut remplacer toute surface équipotentielle. Par exemple, sur la figure \(\PageIndex{2}\), un conducteur sphérique chargé peut remplacer la charge ponctuelle, et le champ électrique et les surfaces de potentiel à l’extérieur de celui-ci serontunchangés, confirmant l’affirmation selon laquelle une distribution sphérique de charges est équivalente à une charge ponctuelle en son centre.
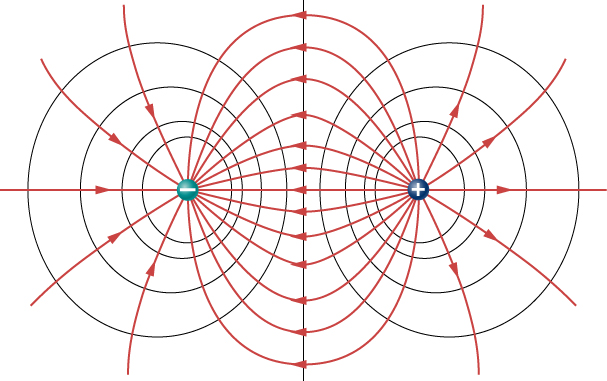
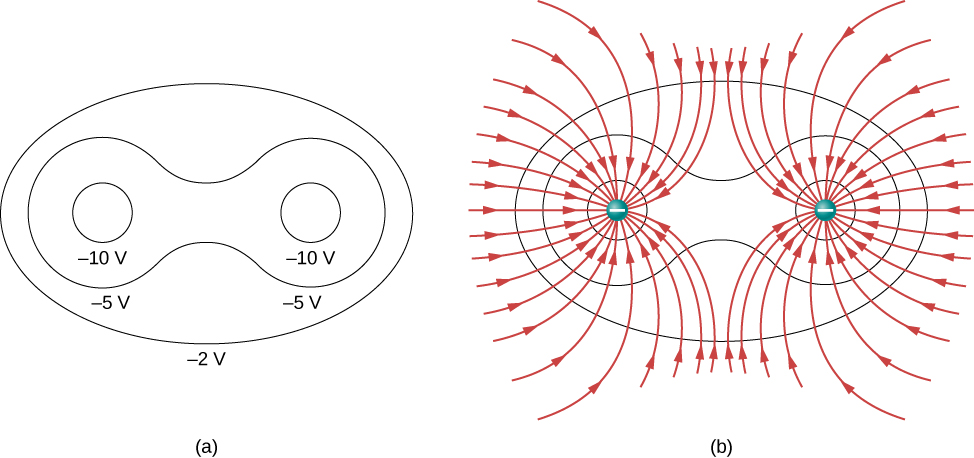
La figure \(\PageIndex{2}\) montre le champ électrique et les lignes équipotentielles pour deux charges égales et opposées. Étant donné les lignes de champ électrique, les lignes équipotentielles peuvent être tracées simplement en les rendant perpendiculaires aux lignes de champ électrique.Inversement, étant donné les lignes équipotentielles, comme dans la figure \(\PageIndex{2a}\), les lignes de champ électrique peuvent être tracées en les rendant perpendiculaires aux équipotentielles, comme dans la figure \(\PageIndex{2b}\).
Pour améliorer votre intuition, nous montrons une variante tridimensionnelle du potentiel dans un système avec deux charges opposées. La figure\(\PageIndex{4}\) présente une carte tridimensionnelle du potentiel électrique, où les lignes de la carte correspondent à des surfaces équipotentielles.La colline se trouve à la charge positive, et le creux à la charge négative. Le potentiel est nul loin des charges.Notez que la coupure à un potentiel particulier implique que les charges sont sur des sphères conductrices avec un rayon fini.
Figure\(\PageIndex{4}\) : Carte de potentiel électrique de deux charges opposées de même amplitude sur des sphères conductrices. Le potentiel est négatif près de la charge négative et positif près de la charge positive. Cette image dynamique est optimisée par CalcPlot3D et peut être visualisée ici.
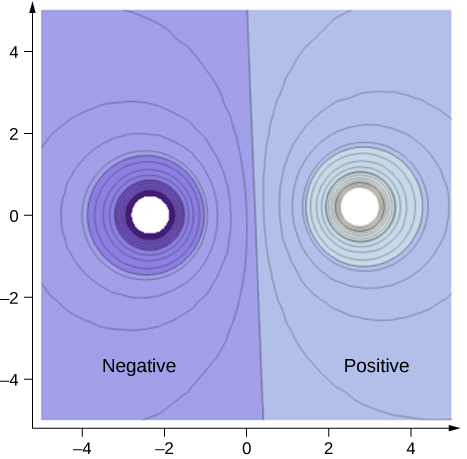
Une carte bidimensionnelle du plan de coupe transversale qui contient les deux charges est représentée sur la figure \(\PageIndex{5}\). La ligne équidistante des deux charges opposées correspond au potentiel zéro, car aux points de la ligne, le potentiel positif de la charge positive annule le potentiel négatif de la charge négative. Les lignes d’équipotentialité dans le plan de coupe sont des boucles fermées, qui ne sont pas nécessairement des cercles, puisqu’en chaque point, le potentiel net est la somme des potentiels de chaque charge.
Note
Voir cette simulation pour observer et modifier les surfaces équipotentielles et les champs électriques pour de nombreuses configurations de charges standard. Il y a beaucoup à explorer.
L’un des cas les plus importants est celui des plaques conductrices parallèles familières illustrées sur la figure \(\PageIndex{6}\). Entre les plaques, les équipotentielles sont uniformément espacées et parallèles. Le même champ pourrait être maintenu en plaçant des plaques conductrices aux lignes équipotentielles aux potentiels indiqués.
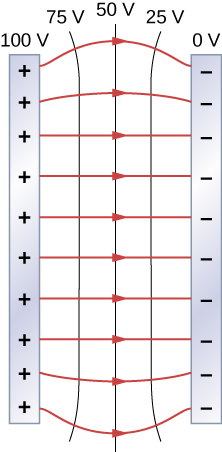
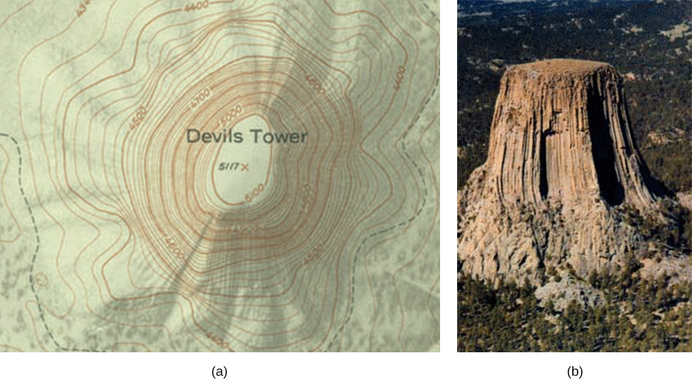
Prenez en considération les plaques parallèles Figure \(\PageIndex{6}\). Elles possèdent des lignes équipotentielles parallèles aux plaques dans l’espace entre elles et régulièrement espacées. La figure \(\PageIndex{6}\) en donne un exemple (avec des valeurs échantillons). Nous pouvons dessiner un ensemble similaire d’isolignes équipotentielles pour la gravité sur les collines. Si la colline a une certaine étendue à la même pente, les isolignes le long de cette étendue seront parallèles les unes aux autres. En outre, dans les régions à pente constante, les isolignes sont régulièrement espacées. Un exemple de lignes topographiques réelles est illustré sur la figure \(\PageIndex{7}\) .
Exemple \(\PageIndex{1}\) : Calcul des lignes équipotentielles
Vous avez vu les lignes équipotentielles d’une charge ponctuelle sur laFigure \(\PageIndex{1}\). Comment les calculer ? Par exemple, si nous avons une \(+10-nC\) charge à l’origine, quelles sont les surfaces équipotentielles auxquelles le potentiel est (a) 100 V, (b) 50 V, (c) 20 V, et (d) 10 V?
Stratégie
Régler l’équation du potentiel d’une charge ponctuelle égale à une constante et résoudre la ou les variables restantes. Calculez ensuite les valeurs si nécessaire.
Solution
Dans \(V = k\dfrac{q}{r}\), laissez V être une constante. La seule variable restante est r ; par conséquent, \(r = k\dfrac{q}{V} =constant\). Ainsi, les surfaces équipotentielles sont des sphères autour de l’origine. Leurs emplacements sont:
- \(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{100 \, V} = 0.90 \, m\);
- \(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{50 \, V} = 1.8 \, m\);
- \N(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{20 \, V} = 4.5 \, m\);
- \N(r = k\dfrac{q}{V} = \left(8.99 \times 10^9 \, Nm^2/C^2\right)\dfrac{(10 \times 10^{-9} C)}{10 \, V} = 9.0 \, m\).
Signification
Cela signifie que les surfaces équipotentielles autour d’une charge ponctuelle sont des sphères de rayon constant, comme montré précédemment, avec des localisations bien définies.
Exemple \(\PageIndex{2}\) : Différence de potentiel entre des plaques parallèles chargées de façon opposée
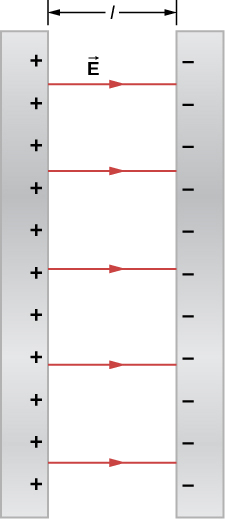
Deux grandes plaques conductrices portent des charges égales et opposées, avec une densité de charge de surface \(\sigma\) de l’ordre de \(6,81 \times10^{-7} C/m\), comme le montre la figure \(\PageIndex{8}\). La séparation entre les plaques est \(l = 6,50 \, mm\).
- Quel est le champ électrique entre les plaques ?
- Quelle est la différence de potentiel entre les plaques ?
- Quelle est la distance entre les plans équipotentiels qui diffèrent de 100 V?
Stratégie
- Puisque les plaques sont décrites comme « grandes » et que la distance entre elles ne l’est pas, nous allons approximer chacune d’elles comme un plan infini, et appliquer le résultat de la loi de Gauss du chapitre précédent.
- Utiliser \(\Delta V_{AB} = – \int_A^B \vec{E} \cdot d\vec{l}\).
- Puisque le champ électrique est constant, trouver le rapport de 100 V sur la différence de potentiel totale ; puis calculer cette fraction de la distance.
Solution
a. Le champ électrique est dirigé de la plaque positive vers la plaque négative comme indiqué sur la figure, et son amplitude est donnée par
&= \dfrac{6.81 \times 10^{-7} C/m^2}{8.85 \times 10^{-12} C^2/N\cdot m^2} \\N &= 7.69 \times 10^4 \, V/m. \end{align*}\]
b. Pour trouver la différence de potentiel \(\Delta V\) entre les plaques, nous utilisons un chemin de la plaque négative à la plaque positive qui est dirigé contre le champ. Le vecteur déplacement \(d\vec{l}\)et le champ électrique \(\vec{E}\) sont antiparallèles donc \(\vec{E}\cdot d\vec{l} = – E \, dl\). La différence de potentiel entre la plaque positive et la plaque négative est alors
&= E \int dl \\\\ &= El \\\\ &= (7.69 \times 10^4V/m)(6.50 \times 10^{-3}m) \\\ &= 500 \, V \end{align*}\]
c. La différence de potentiel totale est de 500 V, donc 1/5 de la distance entre les plaques sera la distance entre des différences de potentiel de 100 V. La distance entre les plaques est de 6,5 mm,il y aura donc 1,3 mm entre les différences de potentiel de 100 V.
Signification
Vous avez maintenant vu un calcul numérique des emplacements deséquipotentiels entre deux plaques parallèles chargées.
Exercice \(\PageIndex{1}\)
Quelles sont les surfaces équipotentielles pour une charge linéaire infinie ?
Réponse
Cylindres infinis de rayon constant, avec la charge linéaire comme axe
Distribution des charges sur les conducteurs
Dans l’exemple \(\PageIndex{1}\) avec une charge ponctuelle, nous avons constaté que les surfaces équipotentielles avaient la forme de sphères, avec la charge ponctuelle au centre. Étant donné qu’une sphère conductrice en équilibre électrostatique est une surface équipotentielle sphérique, nous devrions nous attendre à pouvoir remplacer l’une des surfaces de l’exemple (\PageIndex{2}\) par une sphère conductrice et obtenir une solution identique à l’extérieur de la sphère. L’intérieur sera cependant assez différent.
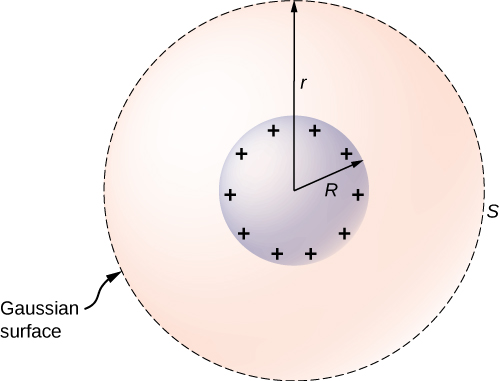
Pour étudier cela, considérez la sphère conductrice isolée de la figure \(\PageIndex{9}\) qui a un rayon R et une surcharge q. Pour trouver le champ électrique à l’intérieur et à l’extérieur de la sphère, notez que la sphère est isolée, donc sa distribution de changement de surface et le champ électrique de cette distribution sont sphériquement symétriques. Nous pouvons donc représenter le champ par \(\vec{E} = E(r)\hat{r}\). Pour calculer \(E(r)\), nous appliquons la loi de Gauss sur une surface sphérique fermée S de rayon r qui est concentrique à la sphère conductrice. Puisque \(r\) est constant et \(\hat{n} = \hat{r}\) sur la sphère,
&=E(r) 4\pi r^2. \end{align}\]
Pour \(r < R\), \(S\) est à l’intérieur du conducteur, donc rappelons-nous de notre étude précédente de la loi de Gauss que \(q_{enc} = 0\) et la loi de Gauss donne \(E(r) = 0\), comme attendu à l’intérieur d’un conducteur à l’équilibre. Si \(r > R\), S entoure le conducteur alors\(q_{enc} = q\). D’après la loi de Gauss,
\
Le champ électrique de la sphère peut donc s’écrire comme
et
Comme prévu, dans la région \(r \geq R\), le champ électrique dû à une charge q placée sur une sphère conductrice isolée de rayon R est identique au champ électrique d’une charge ponctuelle q située au centre de la sphère.
Pour trouver le potentiel électrique à l’intérieur et à l’extérieur de la sphère,notez que pour \(r \geq R\), le potentiel doit être le même que celui d’une charge ponctuelle isolée q située à \(r = 0\),
simplement à cause de la similitude du champ électrique.
Pour \(r < R, \, E = 0\), donc V(r) estconstant dans cette région. Puisque \(V(R) = q/4\pi \epsilon_0 R\),
Nous allons utiliser ce résultat pour montrer que
pour deux sphères conductrices de rayons \(R_1\) et \(R_2\), avec des densités de charge superficielles respectives \(\sigma_1\) et \(\sigma_2\), qui sont reliées par un fil fin, comme illustré sur la Figure\(\PageIndex{10}\). Les sphères sont suffisamment séparées pour que chacune d’elles puisse être traitée comme si elle était isolée (à part le fil).Notez que la connexion par le fil signifie que tout ce système doit être équipotentiel.

Nous venons de voir que le potentiel électrique à la surface d’une sphère conductrice isolée et chargée de rayon Ris
Maintenant, les sphères sont reliées par un conducteur et sont donc au même potentiel ; Par conséquent
\ et
La charge nette d’une sphère conductrice et sa densité de charge superficielle sont liées par \(q = \sigma (4\pi R^2)\). En substituant cette équation à la précédente, nous trouvons
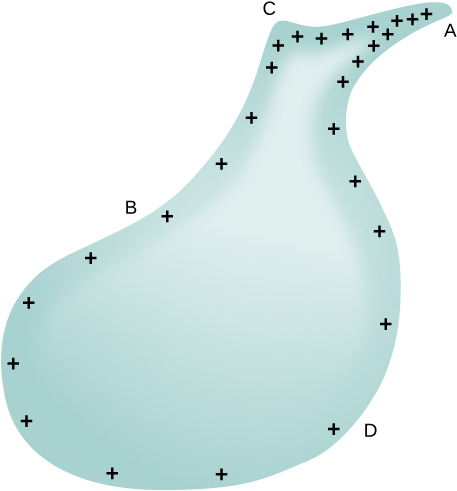
Evidemment, deux sphères reliées par un fil fin ne constituent pas un conducteur typique avec un rayon de courbure variable.Néanmoins, ce résultat fournit au moins une idée qualitativede la façon dont la densité de charge varie sur la surface d’un conducteur. L’équation indique que lorsque le rayon de courbure est grand(points B et D dans la \(\PageIndex{11}\)),\(\sigma\) et E sont petits.
De même, les charges ont tendance à être plus denses là où la courbure de la surface est plus grande, comme le montre la distribution des charges sur un métal de forme bizarre (figure \(\PageIndex{11}\)). La densité de charge de surface est plus élevée aux endroits ayant un petit rayon de courbure qu’aux endroits ayant un grand rayon de courbure.
Une application pratique de ce phénomène est le bâton d’éclairage,qui est simplement une tige métallique mise à la terre avec une extrémité pointue pointant vers le haut. Lorsque des charges positives s’accumulent dans le sol en raison de la présence d’un nuage chargé négativement au-dessus de la tête, le champ électrique autour de l’extrémité pointue devient très important. Lorsque le champ atteint une valeur d’environ \(3,0 \times 10^6 N/C\) (la rigidité diélectrique de l’air), les ions libres dans l’air sont accélérés à des énergies si élevées que leurs collisions avec les molécules d’air ionisent réellement ces dernières. Les électrons libres de l’air qui en résultent traversent alors la tige vers la Terre, neutralisant ainsi une partie de la charge positive. Cela empêche le champ électrique entre le nuage et le sol de devenir suffisamment important pour produire un éclair dans la région autour de la tige.
Une application importante des champs électriques et des équipotentielles concerne le cœur. Le cœur s’appuie sur des signaux électriques pour maintenir son rythme. Le mouvement des signaux électriques provoque la contraction et la relaxation des chambres du cœur. Lorsqu’une personne fait une crise cardiaque, le mouvement de ces signaux électriques peut être perturbé. Un stimulateur cardiaque artificiel et un défibrillateur peuvent être utilisés pour relancer le rythme des signaux électriques. Les lignes équipotentielles autour du cœur, de la région thoracique et de l’axe du cœur sont des moyens utiles pour surveiller la structure et les fonctions du cœur. Un électrocardiogramme (ECG) mesure les petits signaux électriques générés pendant l’activité du cœur.
PheT
Jouer avec cette simulationpour déplacer des charges ponctuelles sur le terrain de jeu, puis visualiser le champ électrique, les tensions, les lignes équipotentielles, etc.
Contributeurs et attributions
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) et Bill Moebs avec de nombreux auteurs collaborateurs. Ce travail est autorisé par OpenStax University Physics sous une licence Creative Commons Attribution License (by 4.0).
.