L’échantillonnage est défini comme suit , « Le processus de mesure des valeurs instantanées d’un signal à temps continu sous une forme discrète. »
L’échantillon est une donnée prise dans l’ensemble des données qui sont continues dans le domaine temporel.
Lorsqu’une source génère un signal analogique et si celui-ci doit être numérisé, ayant des 1 et des 0 c’est-à-dire , Haut ou Bas, le signal doit être discrétisé dans le temps. Cette discrétisation du signal analogique est appelée Echantillonnage.
La figure suivante indique un signal en temps continu x (t) et un signal échantillonné xs (t). Lorsque x (t) est multiplié par un train d’impulsions périodique, on obtient le signal échantillonné xs (t).
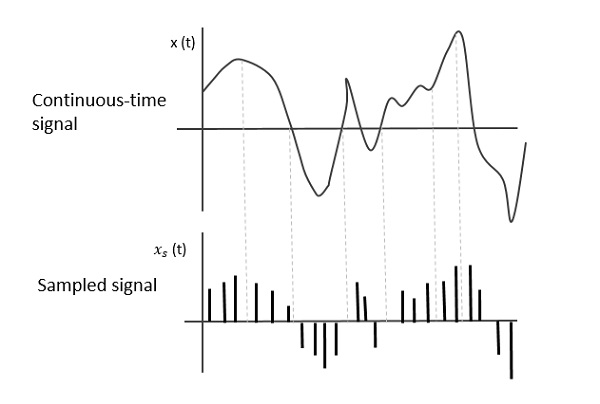
Taux d’échantillonnage
Pour discrétiser les signaux, il faut fixer l’écart entre les échantillons. Cet écart peut être qualifié de période d’échantillonnage Ts.
$Échantillonnage \ : Fréquence = \frac{1}{T_{s}} = f_s$
Où,
-
$T_{s}$ est le temps d’échantillonnage
-
$f_{s}$ est la fréquence d’échantillonnage ou le taux d’échantillonnage
La fréquence d’échantillonnage est l’inverse de la période d’échantillonnage. Cette fréquence d’échantillonnage, peut être appelée simplement Taux d’échantillonnage. Le taux d’échantillonnage désigne le nombre d’échantillons pris par seconde, ou pour un ensemble fini de valeurs.
Pour qu’un signal analogique puisse être reconstruit à partir du signal numérisé, le taux d’échantillonnage doit être fortement considéré. Le taux d’échantillonnage doit être tel que les données du signal de message ne doivent ni être perdues ni se chevaucher. D’où la fixation d’un taux pour cela, appelé taux de Nyquist.
Taux de Nyquist
Supposons qu’un signal soit à bande limitée, sans composante de fréquence supérieure à W Hertz. Autrement dit, W est la fréquence la plus élevée. Pour un tel signal, pour une reproduction efficace du signal original, la fréquence d’échantillonnage doit être égale à deux fois la plus haute fréquence.
Ce qui signifie,
$f_{S} = 2W$
Où,
-
$f_{S}$ est le taux d’échantillonnage
-
W est la plus haute fréquence
Ce taux d’échantillonnage est appelé taux de Nyquist.
Un théorème appelé, Théorème d’échantillonnage, a été énoncé sur la théorie de ce taux de Nyquist.
Théorème d’échantillonnage
Le théorème d’échantillonnage, qui est aussi appelé théorème de Nyquist, délivre la théorie du taux d’échantillonnage suffisant en termes de bande passante pour la classe des fonctions qui sont à bande limitée.
Le théorème d’échantillonnage stipule que, « un signal peut être exactement reproduit s’il est échantillonné à la fréquence fs qui est supérieure à deux fois la fréquence maximale W. »
Pour comprendre ce théorème d’échantillonnage, considérons un signal à bande limitée, c’est-à-dire, un signal dont la valeur est non nulle entre certains -W et W Hertz.
Un tel signal est représenté par $x(f) = 0 pour |f\lvert > W$
Pour le signal à temps continu x (t), le signal à bande limitée dans le domaine fréquentiel, peut être représenté comme le montre la figure suivante.
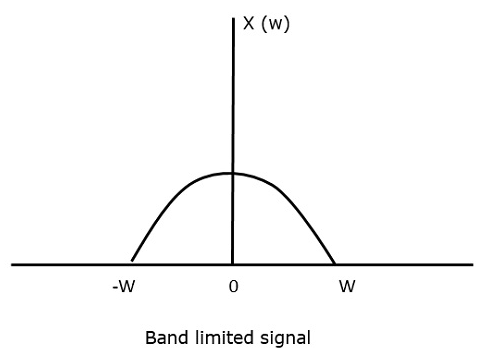
Il nous faut une fréquence d’échantillonnage, une fréquence à laquelle il ne doit pas y avoir de perte d’information, même après échantillonnage. Pour cela, nous avons le taux de Nyquist selon lequel la fréquence d’échantillonnage doit être égale à deux fois la fréquence maximale. C’est le taux critique d’échantillonnage.
Si le signal x(t) est échantillonné au-dessus du taux de Nyquist, le signal original peut être récupéré, et s’il est échantillonné en dessous du taux de Nyquist, le signal ne peut pas être récupéré.
La figure suivante explique un signal, s’il est échantillonné à un taux supérieur à 2w dans le domaine fréquentiel.
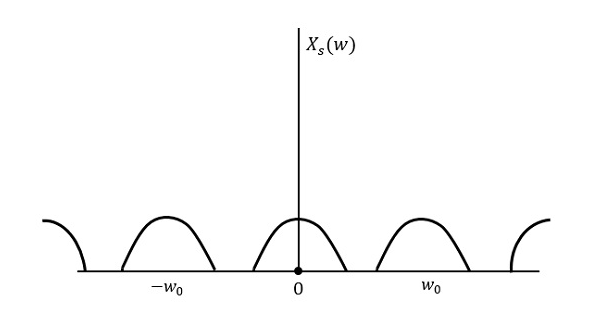
La figure ci-dessus montre la transformée de Fourier d’un signal $x_{s}(t)$. Ici, l’information est reproduite sans aucune perte. Il n’y a pas de mélange et donc la récupération est possible.
La transformée de Fourier du signal $x_{s}(t)$ est
$X_{s}(w) = \frac{1}{T_{s}}\sum_{n = – \infty}^\infty X(w-nw_0)$
Où $T_{s}$ = Période d’échantillonnage et $w_{0} = \frac{2 \pi}{T_s}$
Voyons ce qui se passe si la fréquence d’échantillonnage est égale à deux fois la fréquence la plus élevée (2W)
Ce qui signifie ,
$f_{s} = 2W$
Où,
-
$f_{s}$ est la fréquence d’échantillonnage
-
W est la fréquence la plus élevée
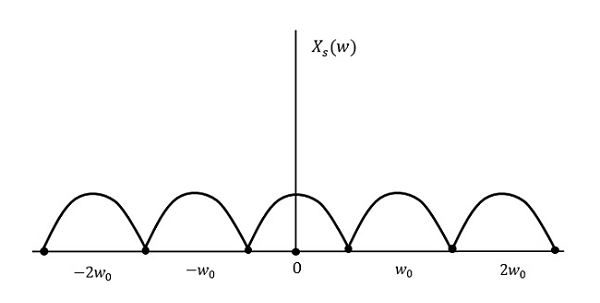
Le résultat sera celui de la figure ci-dessus. L’information est remplacée sans aucune perte. Par conséquent, il s’agit également d’un bon taux d’échantillonnage.
Maintenant, examinons la condition,
$f_{s} Le motif résultant ressemblera à la figure suivante.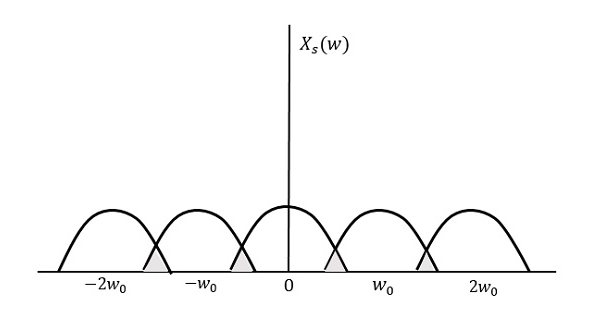
Nous pouvons observer à partir du motif ci-dessus que le chevauchement des informations se fait, ce qui entraîne un mélange et une perte d’informations. Ce phénomène indésirable de chevauchement est appelé Aliasing.
Aliasing
L’Aliasing peut être désigné comme « le phénomène d’une composante haute fréquence dans le spectre d’un signal, prenant l’identité d’une composante basse fréquence dans le spectre de sa version échantillonnée. »
Les mesures correctives prises pour réduire l’effet de l’Aliasing sont –
-
Dans la section d’émission du PCM, un filtre antialiasing passe-bas est employé, avant l’échantillonneur, pour éliminer les composantes haute fréquence, qui sont indésirables.
-
Le signal qui est échantillonné après le filtrage, est échantillonné à un taux légèrement supérieur au taux de Nyquist.
Ce choix d’avoir un taux d’échantillonnage supérieur au taux de Nyquist, permet également de concevoir plus facilement le filtre de reconstruction au niveau du récepteur.
Portée de la transformée de Fourier
On observe généralement que, nous recherchons l’aide des séries et des transformées de Fourier pour analyser les signaux et aussi pour prouver des théorèmes. C’est parce que –
-
La transformée de Fourier est l’extension de la série de Fourier pour les signaux non périodiques.
-
La transformée de Fourier est un outil mathématique puissant qui aide à visualiser les signaux dans différents domaines et aide à analyser les signaux facilement.
-
Tout signal peut être décomposé en termes de somme de sinus et de cosinus en utilisant cette transformée de Fourier.
Dans le prochain chapitre, abordons le concept de quantification.
.