Contenu
Méthode de Newton
La vérité est beaucoup trop compliquée pour permettre autre chose que des approximations.
– John Von Neumann
Trouver une solution avec la géométrie
La méthode de Newton pour résoudre les équations est une autre méthode numérique pour résoudre une équation $f(x) = 0$. Elle est basée sur la géométrie d’une courbe, en utilisant les lignes tangentes à une courbe. En tant que telle, elle nécessite du calcul, en particulier la différenciation.
En gros, l’idée de la méthode de Newton est la suivante . On cherche une solution à $f(x) = 0$. Autrement dit, nous voulons trouver le point en pointillé rouge dans l’image ci-dessous.
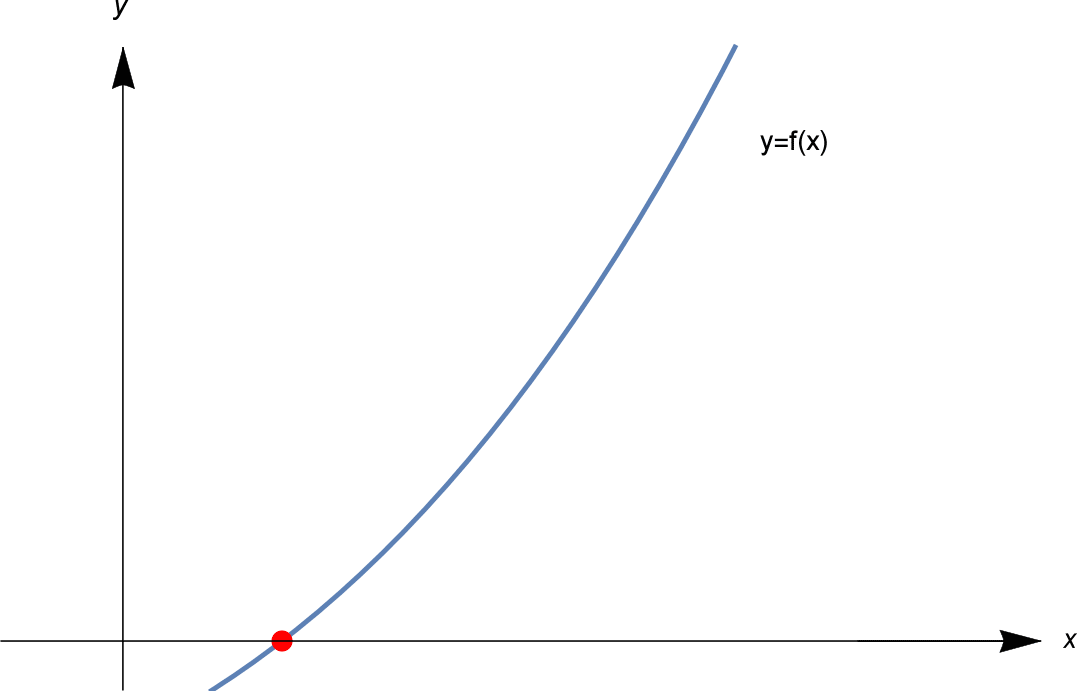
Nous commençons par une estimation initiale $x_1$. Nous calculons $f(x_1)$. Si $f(x_1) = 0$, nous avons beaucoup de chance, et nous avons une solution. Mais il est fort probable que $f(x_1)$ ne soit pas nul. Soit $f(x_1) = y_1$, comme indiqué.
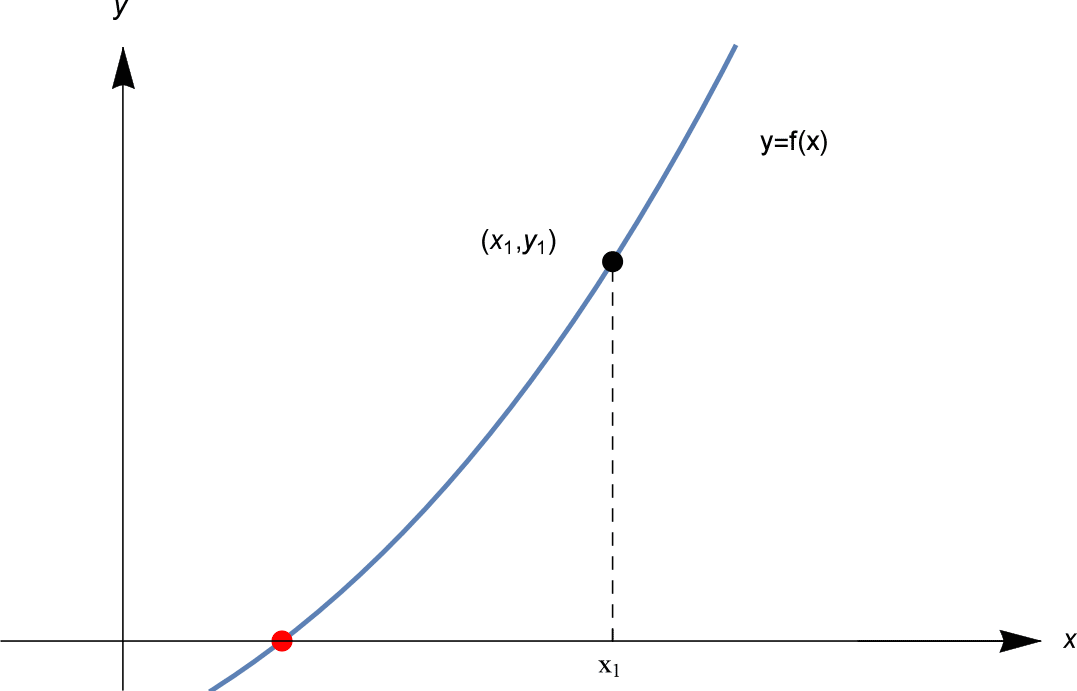
Nous essayons maintenant de trouver une meilleure approximation. Comment trouver cette meilleure estimation ? L’astuce de la méthode de Newton consiste à tracer une ligne tangente au graphique $y=f(x)$ au point $(x_1, y_1)$. Voir ci-dessous.
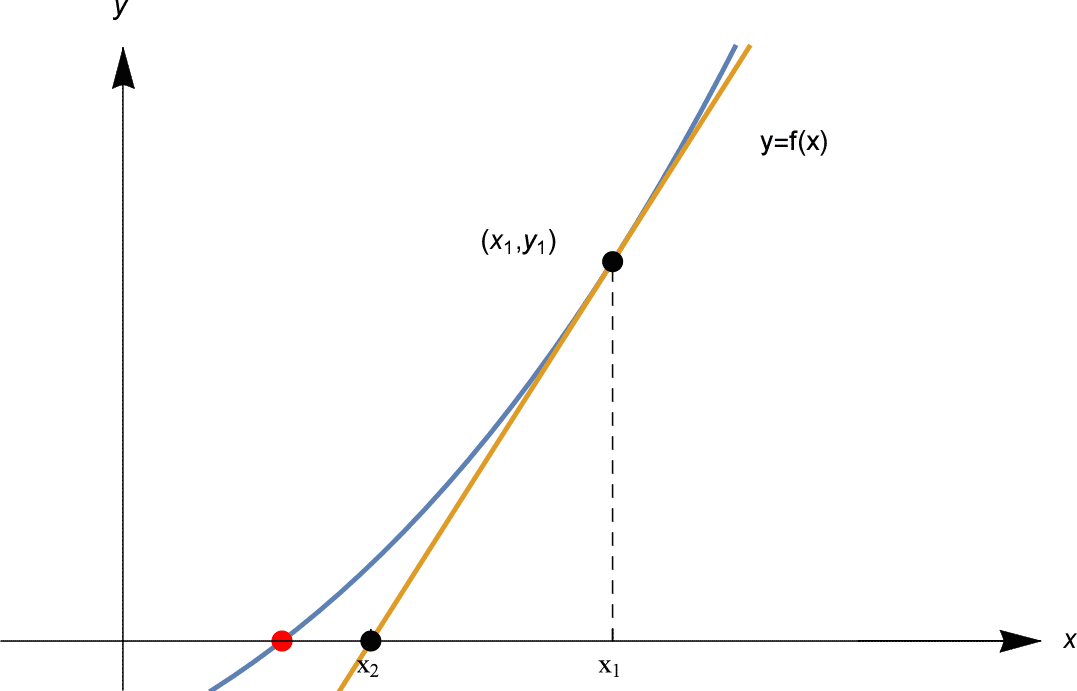
Cette ligne tangente est une bonne approximation linéaire de $f(x)$ près de $x_1$, donc notre prochaine estimation $x_2$ est le point où la ligne tangente coupe l’axe des $x$, comme indiqué ci-dessus.
Nous procédons ensuite en utilisant la même méthode. Nous calculons $y_2 = f(x_2)$ ; si elle est nulle, nous avons terminé. Si ce n’est pas le cas, nous traçons la ligne tangente à $y=f(x)$ à $(x_2, y_2)$, et notre prochaine estimation $x_3$ est le point où cette ligne tangente coupe l’axe $x$. Voir ci-dessous.
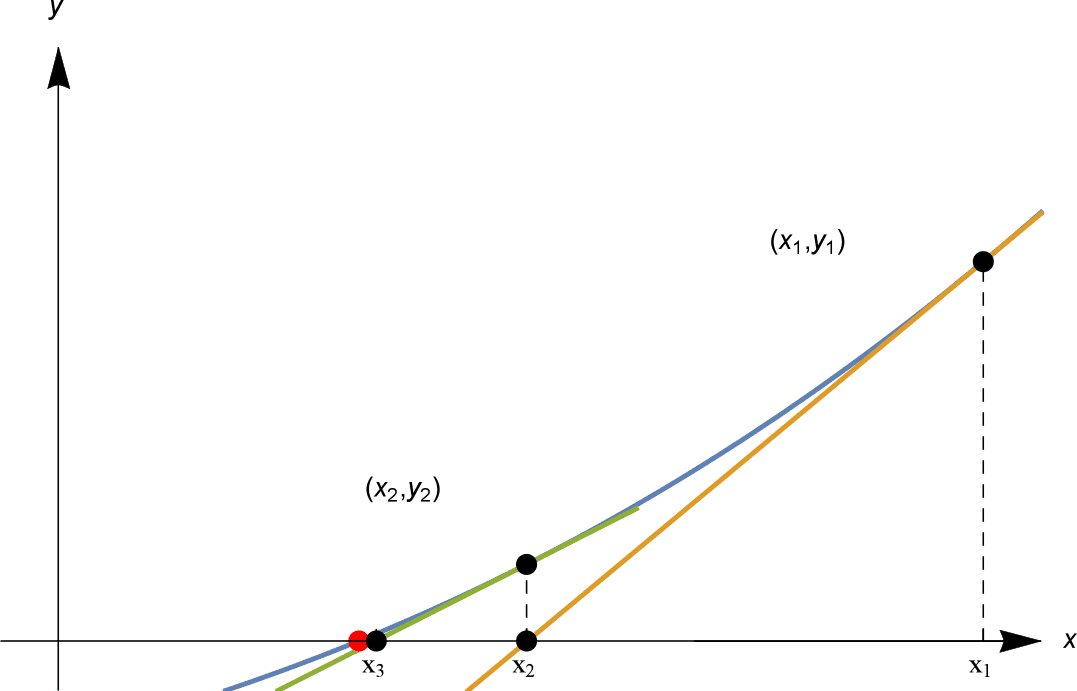
Dans la figure représentée, $x_1, x_2, x_3$ se rapprochent rapidement du point rouge de la solution !
En continuant ainsi, on trouve des points $x_1, x_2, x_3, x_4, \ldots$ approchant une solution. Cette méthode pour trouver une solution est la méthode de Newton.
Comme nous allons le voir, la méthode de Newton peut être une méthode très efficace pour approcher une solution à une équation – quand elle fonctionne.
Le calcul clé
Comme notre introduction ci-dessus vient de le montrer, le calcul clé de chaque étape de la méthode de Newton consiste à trouver où la ligne tangente à $y=f(x)$ au point $(x_1, y_1)$ coupe l’axe $x$.
Trouvons cette intersection $x$. La droite tangente que nous cherchons passe par le point $(x_1, y_1)$ et a pour gradient $f'(x_1)$.
Rappelons que, étant donné la pente $m$ d’une droite, et un point $(x_0, y_0)$ sur celle-ci, la droite a pour équation
\p>Dans notre situation, la droite a pour pente $f'(x_1)$, et passe par $(x_1, y_1)$, donc a pour équation\
Voir le schéma ci-dessous.
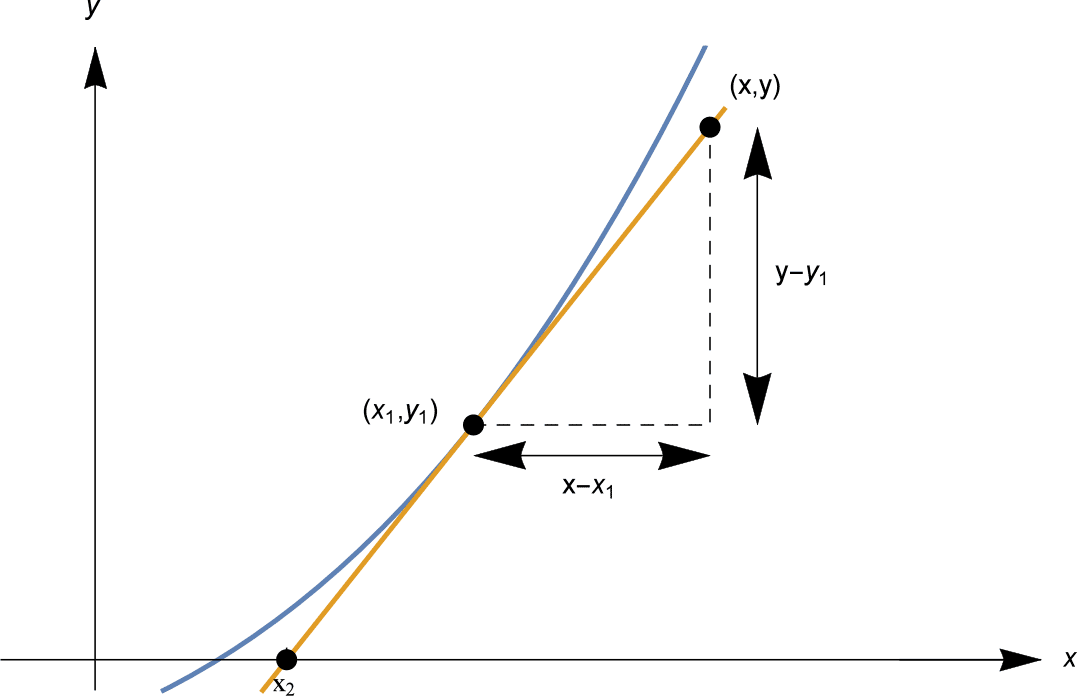
En fixant $y=0$, on trouve l’ordonnée à l’origine de $x$ sous la forme
\
L’algorithme
Nous pouvons maintenant décrire algébriquement la méthode de Newton. En partant de $x_1$, le calcul ci-dessus montre que si l’on construit la ligne tangente au graphe $y=f(x)$ à $x=x_1$, cette ligne tangente a pour $x$-intercept donné par
\
Puis, en partant de $x_2$ on effectue le même calcul, et on obtient l’approximation suivante $x_3$ comme
\p>Le même calcul s’applique à chaque étape : donc à partir de la $n
Méthode de Newton
Laissons $f : \mathbb{R} \rightarrow \mathbb{R}$ soit une fonction différentiable. On cherche une solution de $f(x) = 0$, à partir d’une estimation initiale $x = x_1$.
Au $n$ ème pas, étant donné $x_n$, calculer l’approximation suivante $x_{n+1}$ par
Quelques commentaires sur cet algorithme:
- Souvent, la méthode de Newton fonctionne extrêmement bien, et les $x_n$ convergent rapidement vers une solution. Cependant, il est important de noter que la méthode de Newton ne fonctionne pas toujours. Plusieurs choses peuvent mal tourner, comme nous allons le voir prochainement.
- Notez que si $f(x_n) = 0$, de sorte que $x_n$ est une solution exacte de $f(x) = 0$, alors l’algorithme donne $x_{n+1} = x_n$, et en fait tous les $x_n, x_{n+1}, x_{n+2}, x_{n+3}, \ldots$ seront égaux. Si vous avez une solution exacte, la méthode de Newton restera sur cette solution !
- Alors que la méthode de bissection exige seulement que $f$ soit continue, la méthode de Newton exige que la fonction $f$ soit différentiable. Ceci est nécessaire pour que $f$ ait une ligne tangente.
Utilisation de la méthode de Newton
Comme nous l’avons fait avec la méthode de bissection, approchons quelques constantes bien connues.
Exemple
Utilisez la méthode de Newton pour trouver une solution approchée de $x^2 – 2 = 0$, en partant d’une estimation initiale $x_1 =2$. Après 4 itérations, quelle est la distance entre l’approximation et $\sqrt{2}$ ?
Solution
Disons que $f(x) = x^2 – 2$, donc $f'(x) = 2x$. A l’étape 1, on a $x_1 = 2$ et on calcule $f(x_1) = 2^2 – 2 = 2$ et $f'(x_1) = 4$, donc
A l’étape 2, de $x_2 = \frac{3}{2}$ on calcule $f(x_2) = \frac{1}{4}$ et $f'(x_2) = 3$, donc
A l’étape 3, de $x_3 = \frac{17}{12}$ on a $f(x_3) = \frac{1}{144}$ et $f'(x_3) = \frac{17}{6}$, donc
Au stade 4, à partir de $x_4 = \frac{577}{408}$ on calcule $f(x_4) = \frac{1}{166,464}$ et $f'(x_4) = \frac{577}{204}$, donc
En fait, à 12 décimales près $\sqrt{2} \sim 1.414213562373$. Donc après 4 itérations, la solution approchée $x_5$ est en accord avec $\sqrt{2}$ à 11 décimales près. La différence entre $x_5$ et $\sqrt{2}$ est
\
La méthode de Newton dans l’exemple ci-dessus est beaucoup plus rapide que l’algorithme de bissection ! En seulement 4 itérations, nous avons 11 décimales de précision ! Le tableau suivant illustre le nombre de décimales de précision que nous avons pour chaque $x_n$.
| $n$ | 1$ | 2$ | 3$ | 4$ | $5$ | $6$ | $7$ |
| # précision en décimales | $0$ | 0$ | 2$ | 5$ | 11$ | 23$ | 47$ |
Le nombre de décimales de précision double approximativement à chaque itération !
Exercice 10
(Plus difficile.) Ce problème étudie ce doublement de la précision :
- Calculez d’abord que $x_{n+1} = \frac{x_n}{2}. + \frac{1}{x_n}$ et que, si $y_n = x_n – \sqrt{2}$, alors $y_{n+1} = \frac{y_n^2}{2(\sqrt{2} + y_n)}$.
- Montrer que, si $x_1 > 0$ (resp. $x_1 \sqrt{2}$ (resp. $x_n
- Montrer que si $0
- Montrer que, pour $n \geq 2$, si $x_n$ diffère de $\sqrt{2}$ de moins de $10^{-k}$, alors $x_{n+1}$ diffère de $\sqrt{2}$ de moins de $10^{-2k}$.
Exemple
Trouver une approximation de $\pi$ en utilisant la méthode de Newton pour résoudre $\sin x = 0$ pendant 3 itérations, en partant de $x_1=3$. A combien de décimales près la solution approchée est-elle exacte ?
Solution
Disons que $f(x) = \sin x$, donc $f'(x) = \cos x$. On calcule directement $x_2, x_3, x_4$ en utilisant la formule
\
On calcule directement chaque $x_n$ avec 25 décimales, pour 3 itérations :
\
Avec 25 décimales, $\pi = 3.1415926535897932384626433$ ; $x_4$ s’accorde à 24 décimales.
Dans l’exemple ci-dessus, la convergence est encore plus rapide que pour notre exemple de $\sqrt{2}$. Le nombre de précision des décimales triple grossièrement à chaque itération !
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | |
| # précision du nombre de décimales dans $x_n$ | 0$ | 2$ | $9$ | $24$ | $87$ |
Exercice 11
Trouver toutes les solutions de l’équation $\cos x = x$ jusqu’à 9 décimales en utilisant la méthode de Newton. Comparez la convergence à ce que vous avez obtenu avec la méthode de bissection dans l’exercice 5.
Ce qui peut mal tourner
Alors que la méthode de Newton peut donner des approximations fantastiquement bonnes d’une solution, plusieurs choses peuvent mal tourner. Nous examinons maintenant certains de ces comportements moins heureux.
Le premier problème est que le $x_n$ peut même ne pas être défini !
Exemple
Trouver une solution approchée de $\sin x = 0$ en utilisant la méthode de Newton à partir de $x_1 = \frac{\pi}{2}$.
Solution
On fixe $f(x) = \sin x$, donc $f'(x) = \cos x$. Or $x_2 = x_1 – \frac{f(x_1)}{f'(x_1)}$, mais $f'(x_1) = \cos \frac{\pi}{2} = 0$, donc $x_2$ n’est pas défini, donc aucun des $x_n$ suivants non plus.
Ce problème se pose à chaque fois que $f'(x_n) = 0$. Si $x_n$ est un point stationnaire de $f$, alors la méthode de Newton tente de diviser par zéro – et échoue.
L’exemple suivant illustre que même lorsque les « solutions approchées » $x_n$ existent, elles peuvent ne pas « approcher » très bien une solution.
Exemple
Approximer une solution de $-x^3 + 4x^2 – 2x + 2 = 0$ en utilisant la méthode de Newton à partir de $x_1 = 0$.
Solution
Laissez $f(x) = -x^3 + 4x^2 – 2x + 2$, donc $f'(x) = -3x^2 + 8x – 2$. En partant de $x_1 = 0$, on a
\
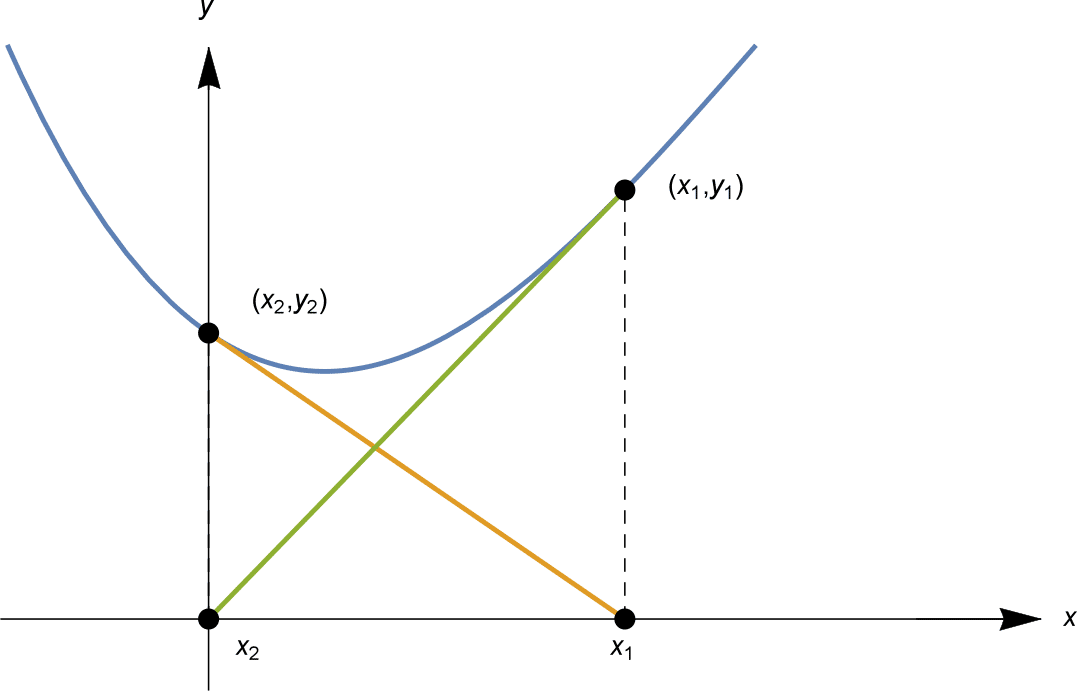
Nous avons maintenant trouvé que $x_3 = x_1 = 0$. Le calcul pour $x_4$ est alors exactement le même que pour $x_2$, donc $x_4 = x_2 = 1$. Ainsi $x_n = 0$ pour tout $n$ impair, et $x_n = 1$ pour tout $n$ pair. Les $x_n$ sont enfermés dans un cycle, alternant entre deux valeurs.
Dans l’exemple ci-dessus, il existe en fait une solution, $x = \frac{1}{3} \left( 4 + \sqrt{10} + \sqrt{100} \right) \sim 3.59867$. Nos « solutions approchées » $x_n$ ne parviennent pas à s’en approcher, faisant plutôt du vélo comme illustré ci-dessous.
Le troisième problème montre que tous les $x_n$ peuvent s’éloigner de plus en plus d’une solution !
Exemple
Trouver une solution approchée de $\arctan x = 0$, en utilisant la méthode de Newton à partir de $x_1 = 3$.
Solution
Laissez $f(x) = \arctan x$, donc $f'(x) = \frac{1}{1+x^2}$. A partir de $x_1 = 3$ on peut calculer successivement $x_2, x_3, \ldots$. On les écrit avec 2 décimales.
\begin{align*}x_2 &= x_1 – \frac{f(x_1)}{f'(x_1)} = 3 – \frac{\arctan 3}{\frac{1}{1+3^2}} = 3 – 10 \arctan 3 \sim -9.49. \x_3 &= x_2 – \frac{f(x_2)}{f'(x_2)} \sim 124.00 \x_4 &= x_3 – \frac{f(x_3)}{f'(x_3)} \sim -23 905,94\end{align*}
Les « approximations » $x_n$ divergent rapidement vers l’infini.

L’exemple ci-dessus peut sembler un peu idiot, car trouver une solution exacte à $\arctan x = 0$ n’est pas difficile : la solution est $x=0$ ! Mais des problèmes similaires se produiront en appliquant la méthode de Newton à toute courbe ayant une forme similaire. Le fait que $f'(x_n)$ soit proche de zéro signifie que la ligne tangente est proche de l’horizontale, et qu’elle peut donc voyager très loin pour arriver à son $x$-intercept de $x_{n+1}$.
Dépendance sensible aux conditions initiales
Parfois, le choix des conditions initiales peut être tout à fait minime, mais conduire à un résultat radicalement différent dans la méthode de Newton.
Pensez à résoudre $f(x) = 2x – 3x^2 + x^3 = 0$. Il est possible de factoriser le cubique, $f(x) = x(x-1)(x-2)$, de sorte que les solutions sont juste $x=0, 1$ et $2$.
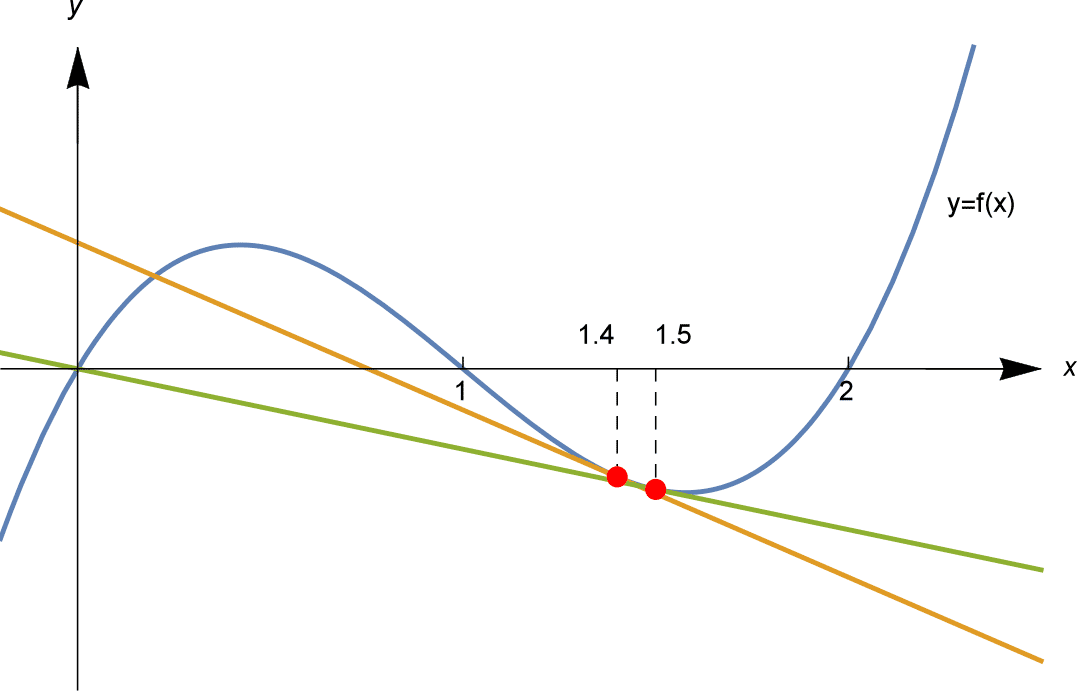
Si nous appliquons la méthode de Newton avec différentes estimations de départ $x_1$, nous pourrions nous retrouver à l’une de ces trois solutions…. ou ailleurs.
Comme illustré ci-dessus, nous appliquons la méthode de Newton en partant de $x_1 = 1,4$ et $x_1 = 1,5$. En partant de $x_1 = 1,4 = \frac{7}{5}$ on calcule, à 6 décimales près,
et les $x_n$ convergent vers la solution $x=1$. Et à partir de $x_1 = 1,5$ on calcule $x_2 = 0$, solution exacte, donc tous les $x_3 = x_4 = \cdots = 0$.
On peut alors se demander : où, entre les estimations initiales $x_1 = 1,4$ et $x_1 = 1.5$, la séquence passe-t-elle de l’approche de $x=1$, à l’approche de $x=0$ ?
Nous constatons que l’estimation initiale $x_1 = 1,45$ se comporte de manière similaire à 1,5$ : la séquence $x_n$ s’approche de la solution $x = 0$. D’autre part, la prise en compte de $x_1 = 1,44$ se comporte de manière similaire à $1,4$ : $x_n$ se rapproche de la solution $x=1$. Le résultat semble basculer quelque part entre les estimations initiales $x_1 = 1,44$ et $x_1 = 1,45$. En effectuant d’autres calculs, nous pouvons préciser davantage et trouver que le changement se produit quelque part entre $x_1 = 1,447$ et $x_1 = 1,448$. Les calculs (à 3 décimales près) à partir de ces valeurs initiales sont présentés dans le tableau ci-dessous.
Alors, si nous essayons $x_1 = 1.4475$, les $x_n$ convergeront-ils vers la solution $x=1$ ou $x=0$ ? La réponse est ni l’un ni l’autre : comme le montre le tableau, il converge vers la solution $x=2$ !
| $x_1$ | 1.4$ | 1,44$ | 1,447$ | 1,4475$ | 1,448$ | 1,45$ | 1.5$ | |
| $x_2$ | 0,754$ | 0,594$ | 0,554$ | 0,551$ | 0.548$ | 0,536$ | 0$ | |
| $x_3$ | 1,036$ | 1,266$ | 1,440$ | 1.458$ | 1,477$ | 1,567$ | 0$ | $x_4$ | 1,000$ | 0,952$ | 0.596$ | 0,484$ | 0,317$ | 9,156$ | 0$ | $x_5$ | 1.000$ | 1,000$ | 1,260$ | 2,370$ | $-0,598$ | $-5.793$ | 0$ |
| $x_6$ | 1,000$ | 1,000$ | 0,956$ | 2,111$ | -0,225$ | 3.562$ | 0$ | |
| $x_7$ | 1,000$ | 1,000$ | 1,000$ | 2,111$ | $-0.225$ | $-3,562$ | 0$ | |
| $x_8$ | 1,000$ | 1,000$ | 1,000$ | 2.000$ | $-0,003$ | $-1,135$ | $0$ | $x_9$ | $1,000$ | $1,000$ | $1.000$ | 2,000$ | 0,000$ | 0,536$ | 0$ | x_{10}$ | 1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.192$ | 0$ |
| $x_{11}$ | 1,000$ | 1,000$ | 1,000$ | 2,000$ | 0,000$ | -0.038$ | 0$ | |
| $x_{12}$ | 1,000$ | 1,000$ | 1,000$ | 2,000$ | 0.000$ | $-0.002$ | $0$ |
De plus, si on essaie $x_1 = 1 + \frac{1}{\sqrt{5}}. \sim 1.447214$, nous trouvons à nouveau un comportement différent ! Il se trouve que,
\
donc $x_1 = x_3$ et les $x_n$ alternent entre ces deux valeurs.
Exercice 12
Vérifier que si $f(x) = 2x – 3x^2 + x^3 = x(x-1)(x-2)$ et $x_1 = 1 + \frac{1}{\sqrt{5}}$, alors $x_2 = 1 – \frac{1}{\sqrt{5}}$ et $x_3 = 1 + \frac{1}{\sqrt{5}} = x_1$.
Il n’y a donc pas de transition simple entre ces valeurs de $x_1$ qui conduisent à la solution $x = 1$ et $x=0$. Le comportement de la méthode de Newton dépend de manière extrêmement sensible de la valeur initiale de $x_1$. En effet, nous n’avons essayé qu’une poignée de valeurs de $x_1$, et n’avons vu que la partie émergée de l’iceberg de ce comportement.
Dans la section Liens vers l’avant, nous examinons ce comportement plus en profondeur, en montrant quelques images de cette dépendance sensible aux conditions initiales, qui est révélatrice du chaos mathématique. Les images illustrant le comportement de la méthode de Newton montrent les détails complexes d’une fractale.
Faire fonctionner la méthode de Newton
En général, il est difficile d’affirmer précisément quand la méthode de Newton fournira de bonnes approximations d’une solution de $f(x) = 0$. Mais nous pouvons faire les remarques suivantes, en résumant nos observations précédentes.
- Si $f'(x_n) = 0$ alors la méthode de Newton échoue immédiatement, car elle tente de diviser par zéro.
- Les « approximations » $x_1, x_2, x_3, \ldots$ peuvent effectuer des cycles, plutôt que de converger vers une solution.
- Les « solutions approximatives » $x_1, x_2, x_3, \ldots$ peuvent même diverger vers l’infini. Ce problème se produit lorsque $f'(x_n)$ est petit, mais pas nul.
- Le comportement de la méthode de Newton peut dépendre de manière extrêmement sensible du choix de $x_1$, et conduire à une dynamique chaotique.
Cependant, une règle empirique utile est la suivante :
- Supposons que vous puissiez esquisser un graphique de $y=f(x)$, et que vous puissiez voir l’emplacement approximatif d’une solution, et que $f'(x)$ ne soit pas trop petit près de cette solution. Alors en prenant $x_1$ près de cette solution, et en s’éloignant des autres solutions ou des points critiques, la méthode de Newton aura tendance à produire $x_n$ qui convergent rapidement vers la solution.
Page suivante – Liens en avant -. Vitesse de l’algorithme de bissection
 |
Ces documents ont été élaborés en collaboration avec la Victorian Curriculum and Assessment Authority. © VCAA et l’Université de Melbourne au nom de l’AMSI 2015 |
Contributeurs Condition d’utilisation |
.ième approximation $x_n$, l’approximation suivante est donnée par\
Formellement, l’algorithme de Newton est le suivant.
Newton’s method
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable function. We seek a solution of $f(x) = 0$, starting from an initial estimate $x = x_1$.
At the $n$’th step, given $x_n$, compute the next approximation $x_{n+1}$ by
\
Some comments about this algorithm:
- Often, Newton’s method works extremely well, and the $x_n$ converge rapidly to a solution. However, it’s important to note that Newton’s method does not always work. Several things can go wrong, as we will see shortly.
- Note that if $f(x_n) = 0$, so that $x_n$ is an exact solution of $f(x) = 0$, then the algorithm gives $x_{n+1} = x_n$, and in fact all of $x_n, x_{n+1}, x_{n+2}, x_{n+3}, \ldots$ will be equal. If you have an exact solution, Newton’s method will stay on that solution!
- While the bisection method only requires $f$ to be continuous, Newton’s method requires the function $f$ to be differentiable. This is necessary for $f$ to have a tangent line.
Using Newton’s method
As we did with the bisection method, let’s approximate some well-known constants.
Example
Use Newton’s method to find an approximate solution to $x^2 – 2 = 0$, starting from an initial estimate $x_1 =2$. After 4 iterations, how close is the approximation to $\sqrt{2}$?
Solution
Let $f(x) = x^2 – 2$, so $f'(x) = 2x$. At step 1, we have $x_1 = 2$ and we calculate $f(x_1) = 2^2 – 2 = 2$ and $f'(x_1) = 4$, so
\
At step 2, from $x_2 = \frac{3}{2}$ we calculate $f(x_2) = \frac{1}{4}$ and $f'(x_2) = 3$, so
\
At step 3, from $x_3 = \frac{17}{12}$ we have $f(x_3) = \frac{1}{144}$ and $f'(x_3) = \frac{17}{6}$, so
\
At step 4, from $x_4 = \frac{577}{408}$ we calculate $f(x_4) = \frac{1}{166,464}$ and $f'(x_4) = \frac{577}{204}$, so
\
In fact, to 12 decimal places $\sqrt{2} \sim 1.414213562373$. So after 4 iterations, the approximate solution $x_5$ agrees with $\sqrt{2}$ to 11 decimal places. The difference between $x_5$ and $\sqrt{2}$ is
\
Newton’s method in the above example is much faster than the bisection algorithm! In only 4 iterations we have 11 decimal places of accuracy! The following table illustrates how many decimal places of accuracy we have in each $x_n$.
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
| # decimal places accuracy in | $0$ | $0$ | $2$ | $5$ | $11$ | $23$ | $47$ |
The number of decimal places of accuracy approximately doubles with each iteration!
Exercise 10
(Harder.) This problem investigates this doubling of accuracy:
- First calculate that $x_{n+1} = \frac{x_n}{2} + \frac{1}{x_n}$ and that, if $y_n = x_n – \sqrt{2}$, then $y_{n+1} = \frac{y_n^2}{2(\sqrt{2} + y_n)}$.
- Show that, if $x_1 > 0$ (resp. $x_1 \sqrt{2}$ (resp. $x_n
- Show that if $0
- Show that, for $n \geq 2$, if $x_n$ differs from $\sqrt{2}$ by less than $10^{-k}$, then $x_{n+1}$ differs from $\sqrt{2}$ by less than $10^{-2k}$.
Example
Find an approximation to $\pi$ by using Newton’s method to solve $\sin x = 0$ for 3 iterations, starting from $x_1=3$. To how many decimal places is the approximate solution accurate?
Solution
Let $f(x) = \sin x$, so $f'(x) = \cos x$. We compute $x_2, x_3, x_4$ directly using the formula
\
We compute directly each $x_n$ to 25 decimal places, for 3 iterations:
\
To 25 decimal places, $\pi = 3.1415926535897932384626433$; $x_4$ agrees to 24 places.
In the above example, convergence is even more rapid than for our $\sqrt{2}$ example. The number of decimal places accuracy roughly triples with each iteration!
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ |
| # decimal places accuracy in $x_n$ | $0$ | $2$ | $9$ | $24$ | $87$ |
Exercise 11
Find all solutions to the equation $\cos x = x$ to 9 decimal places using Newton’s method. Compare the convergence to what you obtained with the bisection method in exercise 5.
What can go wrong
While Newton’s method can give fantastically good approximations to a solution, several things can go wrong. We now examine some of this less fortunate behaviour.
The first problem is that the $x_n$ may not even be defined!
Example
Find an approximate solution to $\sin x = 0$ using Newton’s method starting from $x_1 = \frac{\pi}{2}$.
Solution
We set $f(x) = \sin x$, so $f'(x) = \cos x$. Now $x_2 = x_1 – \frac{f(x_1)}{f'(x_1)}$, but $f'(x_1) = \cos \frac{\pi}{2} = 0$, so $x_2$ is not defined, hence nor are any subsequent $x_n$.
This problem occurs whenever when $f'(x_n) = 0$. If $x_n$ is a stationary point of $f$, then Newton’s method attempts to divide by zero — and fails.
The next example illustrates that even when the « approximate solutions » $x_n$ exist, they may not « approximate » a solution very well.
Example
Approximate a solution to $-x^3 + 4x^2 – 2x + 2 = 0$ using Newton’s method from $x_1 = 0$.
Solution
Let $f(x) = -x^3 + 4x^2 – 2x + 2$, so $f'(x) = -3x^2 + 8x – 2$. Starting from $x_1 = 0$, we have
\
We have now found that $x_3 = x_1 = 0$. The computation for $x_4$ is then exactly the same as for $x_2$, so $x_4 = x_2 = 1$. Thus $x_n = 0$ for all odd $n$, and $x_n = 1$ for all even $n$. The $x_n$ are locked into a cycle, alternating between two values.
In the above example, there is actually a solution, $x = \frac{1}{3} \left( 4 + \sqrt{10} + \sqrt{100} \right) \sim 3.59867$. Our « approximate solutions » $x_n$ fail to approximate it, instead cycling as illustrated below.

The third problem shows that all $x_n$ can get further and further away from a solution!
Example
Find an approximate solution to $\arctan x = 0$, using Newton’s method starting at $x_1 = 3$.
Solution
Let $f(x) = \arctan x$, so $f'(x) = \frac{1}{1+x^2}$. From $x_1 = 3$ we can compute successively $x_2, x_3, \ldots$. We write them to 2 decimal places.
\begin{align*}x_2 &= x_1 – \frac{f(x_1)}{f'(x_1)} = 3 – \frac{\arctan 3}{\frac{1}{1+3^2}} = 3 – 10 \arctan 3 \sim -9.49. \\x_3 &= x_2 – \frac{f(x_2)}{f'(x_2)} \sim 124.00 \\x_4 &= x_3 – \frac{f(x_3)}{f'(x_3)} \sim -23,905.94\end{align*}
The « approximations » $x_n$ rapidly diverge to infinity.

The above example may seem a little silly, since finding an exact solution to $\arctan x = 0$ is not difficult: the solution is $x=0$! But similar problems will happen applying Newton’s method to any curve with a similar shape. The fact that $f'(x_n)$ is close to zero means the tangent line is close to horizontal, and so may travel far away to arrive at its $x$-intercept of $x_{n+1}$.
Sensitive dependence on initial conditions
Sometimes the choice of initial conditions can be ever so slight, yet lead to a radically different outcome in Newton’s method.
Consider solving $f(x) = 2x – 3x^2 + x^3 = 0$. It’s possible to factorise the cubic, $f(x) = x(x-1)(x-2)$, so the solutions are just $x=0, 1$ and $2$.

If we apply Newton’s method with different starting estimates $x_1$, we might end up at any of these three solutions… or somewhere else.
As illustrated above, we apply Newton’s method starting from $x_1 = 1.4$ and $x_1 = 1.5$. Starting from $x_1 = 1.4 = \frac{7}{5}$ we compute, to 6 decimal places,
\
and the $x_n$ converge to the solution $x=1$. And starting from $x_1 = 1.5$ we compute $x_2 = 0$, an exact solution, so all $x_3 = x_4 = \cdots = 0$.
We might then ask: where, between the initial estimates $x_1 = 1.4$ and $x_1 = 1.5$, does the sequence switch from approaching $x=1$, to approaching $x=0$?
We find that the the initial estimate $x_1 = 1.45$ behaves similarly to $1.5$: the sequence $x_n$ approaches the solution $x = 0$. On the other hand, taking $x_1 = 1.44$ behaves similarly to $1.4$: $x_n$ approaches the solution $x=1$. The outcome seems to switch somewhere between the initial estimates $x_1 = 1.44$ and $x_1 = 1.45$. With some more computations, we can narrow down further and find that the switch happens somewhere between $x_1 = 1.447$ and $x_1 = 1.448$. The computations (to 3 decimal places) from these initial values are shown in the table below.
So, if we try $x_1 = 1.4475$, will the $x_n$ converge to the solution $x=1$ or $x=0$? The answer is neither: as shown in the table, it converges to the solution $x=2$!
| $x_1$ | $1.4$ | $1.44$ | $1.447$ | $1.4475$ | $1.448$ | $1.45$ | $1.5$ |
| $x_2$ | $0.754$ | $0.594$ | $0.554$ | $0.551$ | $0.548$ | $0.536$ | $0$ |
| $x_3$ | $1.036$ | $1.266$ | $1.440$ | $1.458$ | $1.477$ | $1.567$ | $0$ |
| $x_4$ | $1.000$ | $0.952$ | $0.596$ | $0.484$ | $0.317$ | $-9.156$ | $0$ |
| $x_5$ | $1.000$ | $1.000$ | $1.260$ | $2.370$ | $-0.598$ | $-5.793$ | $0$ |
| $x_6$ | $1.000$ | $1.000$ | $0.956$ | $2.111$ | $-0.225$ | $-3.562$ | $0$ |
| $x_7$ | $1.000$ | $1.000$ | $1.000$ | $2.111$ | $-0.225$ | $-3.562$ | $0$ |
| $x_8$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $-0.003$ | $-1.135$ | $0$ |
| $x_9$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.536$ | $0$ |
| $x_{10}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.192$ | $0$ |
| $x_{11}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.038$ | $0$ |
| $x_{12}$ | $1.000$ | $1.000$ | $1.000$ | $2.000$ | $0.000$ | $-0.002$ | $0$ |
Furthermore, if we try $x_1 = 1 + \frac{1}{\sqrt{5}} \sim 1.447214$, we find different behaviour again! As it turns out,
\
so $x_1 = x_3$ and the $x_n$ alternate between these two values.
Exercise 12
Verify that if $f(x) = 2x – 3x^2 + x^3 = x(x-1)(x-2)$ and $x_1 = 1 + \frac{1}{\sqrt{5}}$, then $x_2 = 1 – \frac{1}{\sqrt{5}}$ and $x_3 = 1 + \frac{1}{\sqrt{5}} = x_1$.
So there is no simple transition from those values of $x_1$ which lead to the solution $x = 1$ and $x=0$. The behaviour of Newton’s method depends extremely sensitively on the initial $x_1$. Indeed, we have only tried only a handful of values for $x_1$, and have only seen the tip of the iceberg of this behaviour.
In the Links Forward section we examine this behaviour further, showing some pictures of this sensitive dependence on initial conditions, which is indicative of mathematical chaos. Pictures illustrating the behaviour of Newton’s method show the intricate detail of a fractal.
Getting Newton’s method to work
In general, it is difficult to state precisely when Newton’s method will provide good approximations to a solution of $f(x) = 0$. But we can make the following notes, summarising our previous observations.
- If $f'(x_n) = 0$ then Newton’s method immediately fails, as it attempts to divide by zero.
- The « approximations » $x_1, x_2, x_3, \ldots$ can cycle, rather than converging to a solution.
- The « approximate solutions » $x_1, x_2, x_3, \ldots$ can even diverge to infinity. This problem happens when $f'(x_n)$ is small, but not zero.
- The behaviour of Newton’s method can depend extremely sensitively on the choice of $x_1$, and lead to chaotic dynamics.
However, a useful rule of thumb is as follows:
- Suppose you can sketch a graph of $y=f(x)$, and you can see the approximate location of a solution, and $f'(x)$ is not too small near that solution. Then taking $x_1$ near that solution, and away from other solutions or critical points, Newton’s method will tend to produce $x_n$ which converge rapidly to the solution.
Next page – Links forward – Speed of the bisection algorithm
 |
These materials have been developed in collaboration with the Victorian Curriculum and Assessment Authority. © VCAA and The University of Melbourne on behalf of AMSI 2015 |
Contributors Term of use |