La règle de Cramer est une autre méthode qui permet de résoudre des systèmes d’équations linéaires en utilisant des déterminants.
En termes de notations, une matrice est un tableau de nombres entouré de crochets tandis que le déterminant est un tableau de nombres entouré de deux barres verticales.
Notations
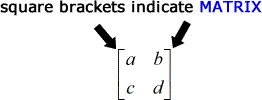
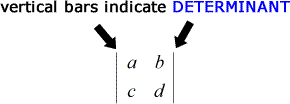
La formule pour trouver le déterminant d’une matrice 2 x 2 est très simple.
Faisons un rapide tour d’horizon :
Le déterminant d’une matrice 2 x 2
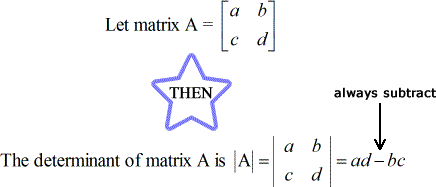
Exemples rapides de la façon de trouver les déterminants d’une matrice 2 x 2
Exemple 1 : Trouvez le déterminant de la matrice A ci-dessous.
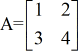
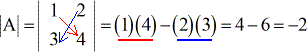
Exemple 2 : Trouvez le déterminant de la matrice B ci-dessous.
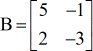
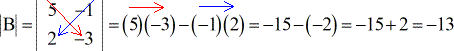
Exemple 3 : Trouvez le déterminant de la matrice C ci-dessous.
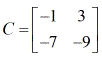
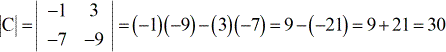
Après avoir su comment trouver le déterminant d’une matrice 2 x 2, vous êtes maintenant prêt à apprendre les procédures ou les étapes sur la façon d’utiliser la règle de Cramer. C’est parti !
Règle de Cramer pour les systèmes d’équations linéaires à deux variables
- Donné un système linéaire

- Attribuer des noms pour chaque matrice
matrice de coefficients :
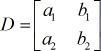
X – matrice :
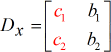
Y – matrice :
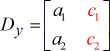
Pour résoudre la variable x.
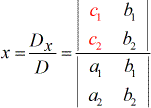
Pour résoudre la variable y.
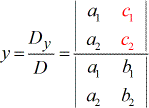
Quelques points à considérer en regardant la formule :
1) Les colonnes de \large{x}, \large{y}, et les termes constants \large{c} sont obtenus comme suit :
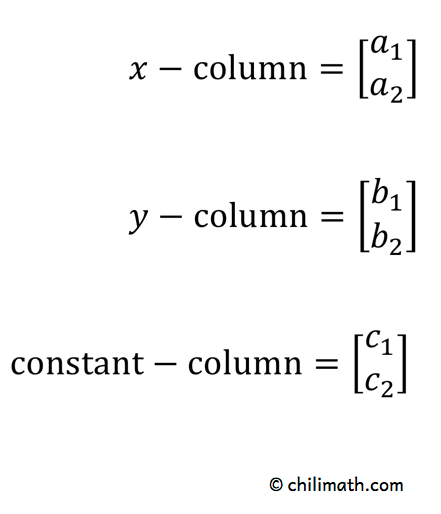
2) Les deux dénominateurs dans la résolution de \large{x} et \large{y} sont les mêmes. Ils proviennent des colonnes de \large{x} et \large{y}.
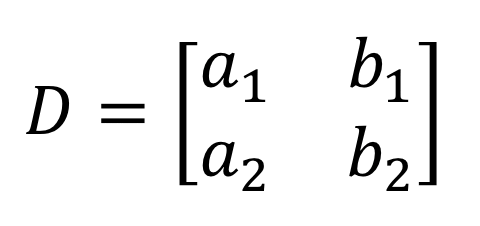
3) En regardant le numérateur dans la résolution de \large{x}, les coefficients de la colonne \large{x} sont remplacés par la colonne constante (en rouge).
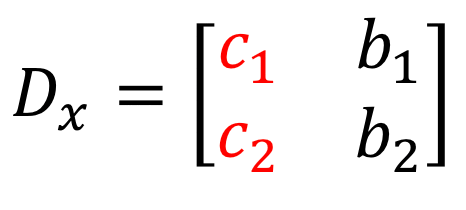
4) De la même manière, pour résoudre \large{y}, on remplace les coefficients de \large{y}-colonne par la colonne constante (en rouge).
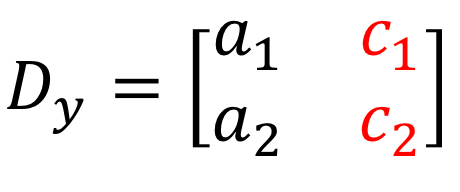
Exemples de la façon de . Résoudre des systèmes d’équations linéaires à deux variables en utilisant la règle de Cramer
Exemple 1 : Résoudre le système à deux variables par la règle de Cramer
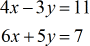
Commencez par extraire les trois matrices pertinentes : coefficient, \large{x}, et \large{y}. Résolvez ensuite chaque déterminant correspondant.
- Pour la matrice de coefficient
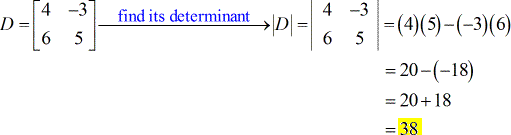
- Pour X – matrice

- Pour Y – matrice

Une fois les trois déterminants calculés, il est temps de résoudre les valeurs de \large{x} et \large{y} en utilisant la formule ci-dessus.
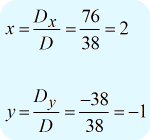
Je peux écrire la réponse finale sous la forme \large{\left( {x,y} \right) = \left( {2, – 1} \right)}.
Exemple 2 : Résoudre le système à deux variables par la règle de Cramer
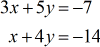
Établissez vos matrices de coefficients, \large{x} et \large{y} à partir du système d’équations linéaires donné. Calculez ensuite leurs déterminants en conséquence.
Rappellez-vous que nous soustrayons toujours les produits des entrées diagonales.
- Pour la matrice des coefficients (utilisez les coefficients des variables x et y)
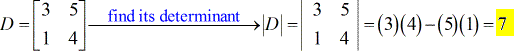
- Pour la matrice X – (remplacer la colonne x par la colonne constante)
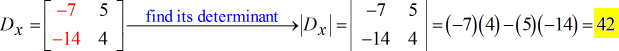
- Pour la matrice Y – (remplacer la colonne y par la colonne constante)
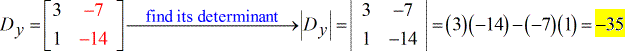
J’espère que vous êtes à l’aise pour calculer le déterminant d’une matrice à 2 dimensions. Pour finalement résoudre les variables requises, j’obtiens les résultats suivants…
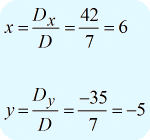
En écrivant la réponse finale en notation ponctuelle, j’ai obtenu \large{\left( {x,y} \right) = \left( {6, – 5} \right)}.
Exemple 3 : Résoudre le système à deux variables par la règle de Cramer
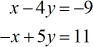
Ce problème peut en fait être résolu assez facilement par la méthode d’élimination. En effet, les coefficients de la variable x sont » les mêmes » mais seulement de signes opposés ( +1 et -1 ). Pour résoudre ce problème à l’aide de la méthode d’élimination, vous ajoutez les colonnes correspondantes et la variable x disparaît, ce qui vous laisse avec une équation à une étape dans \large{y}. Je mentionne ceci parce que chaque technique a ses défauts et qu’il est préférable de choisir la plus efficace. Clarifiez toujours auprès de votre professeur si vous pouvez utiliser une autre approche lorsque la méthode n’est pas spécifiée sur un problème donné.
En tout cas, puisque nous apprenons à résoudre par la règle de Cramer, allons-y et travaillons avec cette méthode.
Je vais construire trois matrices ( coefficient, \large{x} et \large{y}) et évaluer leurs déterminants correspondants.
- Pour la matrice coefficient
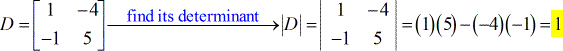
- Pour la matrice X – ( écrite en majuscule D avec l’indice x )
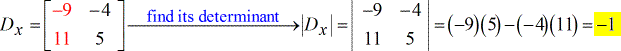
- Pour la matrice Y – (écrite en majuscule D avec l’indice y)
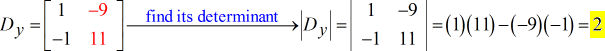
Après avoir obtenu les valeurs des trois déterminants requis, je vais calculer \large{x} et \large{y} comme suit.
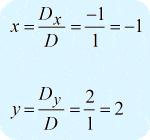
La réponse finale sous forme ponctuelle est \large{\left( {x,y} \right) = \left( { – 1,2} \right)} .
Exemple 4 : Résoudre par la règle de Cramer le système à deux variables
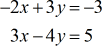
Puisque nous avons déjà parcouru quelques exemples, je vous suggère d’essayer ce problème par vous-même. Ensuite, comparez vos réponses à la solution ci-dessous.
Si vous y arrivez du premier coup, cela signifie que vous êtes en train de devenir un » pro » en ce qui concerne la règle de Cramer. Si ce n’est pas le cas, essayez de comprendre ce qui n’a pas fonctionné et apprenez à ne pas commettre la même erreur la prochaine fois. C’est ainsi que vous deviendrez meilleur en mathématiques. Étudiez de nombreux types de problèmes et surtout, faites beaucoup de pratique indépendante.
- Pour la matrice des coefficients
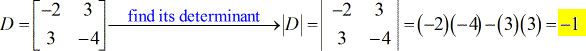
- Pour X – matrice
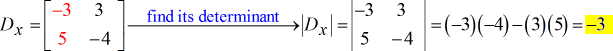
- Pour la matrice Y
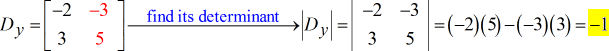
Vous devriez obtenir la réponse ci-dessous…
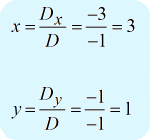
Exemple 5 : Résoudre le système à deux variables par la règle de Cramer
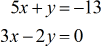
Pour notre dernier exemple, j’ai inclus un zéro dans la colonne des constantes. Chaque fois que vous voyez le nombre zéro dans la colonne constante, je recommande vivement d’utiliser la règle de Cramer pour résoudre le système d’équations linéaires. Pourquoi ? Parce que le calcul des déterminants des matrices \large{x} et \large{y} devient drastiquement super facile. Vérifiez vous-même !
- Pour la matrice des coefficients
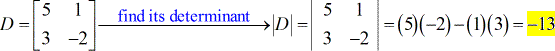
- Pour X – matrice
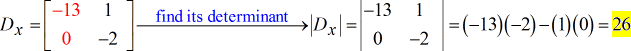
- Pour la matrice Y
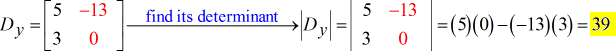
La solution finale de ce problème est
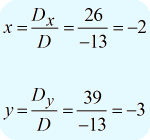
Pratique avec les feuilles de travail
Vous pourriez également être intéressé par:
La règle de Cramer 3×3
.