Introduction
Les propriétés élastiques jouent un rôle important dans un certain nombre de processus membranaires, comme par exemple la fusion membranaire (Chernomordik et Kozlov, 2008) et les modulations des activités des canaux membranaires (Schmidt et MacKinnon, 2008 ; Sansom et Biggin, 2010 ; Mashaghi et al., 2013b). Dans les cellules, les membranes externes sont soutenues par les réseaux d’actine sous-jacents. La contrainte mécanique est alors dominée par le cytosquelette d’actine associé à des échelles de longueur supérieures à la taille des mailles du réseau d’actine (30-300 nm) (Morone et al., 2006). Sur les petites échelles de longueur, cependant, la contribution de la bicouche lipidique sera dominante. A ce titre, des efforts ont été faits pour étudier les propriétés mécaniques de patchs bicouches de dimensions proches du maillage du cytosquelette d’actine (Claesson et al., 2011).
Lorsqu’on considère une membrane comme un corps bidimensionnel, c’est-à-dire en négligeant son épaisseur, ses propriétés mécaniques en l’absence d’anisotropies peuvent être caractérisées par deux constantes élastiques selon la théorie de l’élasticité continue. Dans la pratique courante de la caractérisation des matériaux, ces paramètres sont généralement le module d’Young et le coefficient de Poisson. Des estimations du module de Young des membranes ont été fournies par des expériences (Tierney et al., 2005 ; Popescu et al., 2006). Cependant, la mesure du coefficient de Poisson n’est pas simple, en raison de la faible épaisseur des membranes de l’ordre du nanomètre (Mitchell et al., 2003 ; Martins et al., 2009). D’un point de vue théorique, les propriétés mécaniques des membranes lipidiques sont généralement étudiées sur la base du Hamiltonien de Helfrich. La principale quantité physique obtenue à partir de ces études est la rigidité en flexion. Le module de Young et le coefficient de Poisson sont liés par des formules qui intègrent la rigidité en flexion, mais ni le module de Young ni le coefficient de Poisson n’ont été déterminés séparément jusqu’à présent.
Des simulations et des modèles théoriques ont été utilisés pour fournir des informations importantes sur les propriétés élastiques (Goetz et Lipowsky, 1998 ; Lindahl et Edholm, 2001 ; Ayton et al., 2002) et visqueuses des bicouches lipidiques (Jeon et Voth, 2005). L’étude des propriétés mécaniques des films minces ne se limite pas aux biomembranes et représente un domaine de recherche actif en science des matériaux. Des efforts ont été déployés pour prédire le coefficient de Poisson de films constitués de divers matériaux au moyen de simulations informatiques. Par exemple, Galvao et al. ont utilisé des simulations de dynamique moléculaire utilisant des potentiels d’ordre de liaison empiriques réactifs pour étudier les propriétés mécaniques des nanorubans de graphène (Martins et Galvao, 2010). Baughman et al. ont proposé un modèle pour estimer le coefficient de Poisson des réseaux de fibres et l’ont appliqué avec succès aux feuilles de nanotubes de carbone (buckypaper) (Hall et al., 2008).
Dans ce travail, nous introduisons une méthode pour déterminer le coefficient de Poisson ν dans les simulations et l’appliquons au modèle de membrane lipidique à gros grains, qui a été introduit par Lenz et Schmid (2005). Cette méthode est générale et applicable à toute autre surface. Après avoir déterminé la rigidité à la flexion kc à partir du spectre de puissance des fluctuations de la hauteur de la membrane, nous sommes en mesure de calculer le module d’Young E.
Matériaux et méthodes
Des simulations Monte Carlo de bicouches lipidiques avec des conditions limites périodiques dans les directions latérales ont été effectuées pour le modèle à gros grains introduit par Lenz et Schmid (2005). Dans ce modèle, on considère des amphiphiles à queue unique, qui sont représentés par six billes de queue et une bille de tête légèrement plus grande (avec un rapport de taille de 1-1,1). Les perles appartenant à une même molécule sont reliées par des ressorts non linéaires élastiques finiment extensibles (FENE) (Grest et Kremer, 1986) avec un potentiel d’étirement des liaisons Figure 1 :
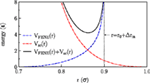
Figure 1. Interactions appliquées dans le modèle.
Ici r est la distance entre les billes adjacentes, νFENE caractérise la force du ressort, r0 est la longueur de liaison optimale (pas d’étirement), et Δrm est la distance d’étirement maximale. La rigidité des queues est prise en compte par un potentiel harmonique d’angle de liaison
où θijk est l’angle de liaison associé à trois perles adjacentes. Les billes non liées appartenant à la même molécule et les billes appartenant à des molécules différentes interagissent via un potentiel de noyau mou :
où θ(.) est la fonction de pas de Heaviside. Les molécules de solvant sont représentées par un modèle fantôme de billes qui interagissent avec les billes lipidiques via VSC(r) (avec les mêmes paramètres que les billes de tête) mais n’interagissent pas avec elles-mêmes. Tous les paramètres du modèle ont été choisis en fonction du modèle référencé (Lenz et Schmid, 2005) et sont résumés dans le tableau 1.

Tableau 1. Potentiels d’interaction du modèle référencé et paramètres correspondants.
Les bicouches lipidiques présentent un riche spectre de structures et de transitions de phase (Nagle et Tristram-Nagle, 2000 ; Illya et al., 2005 ; Seto et al., 2008 ; Thakkar et al., 2011). L’état fluide à haute température est caractérisé par un arrangement désordonné des queues de lipides et une mobilité lipidique comparativement élevée. Lors du refroidissement, cet état fluide subit une transition de phase vers un état de gel, où les molécules lipidiques sont plus ordonnées et ont une mobilité plus faible. D’autres phases possibles sont la phase interdigitée, dans laquelle les queues lipidiques de monocouches opposées s’interpénètrent.
En balayant le diagramme de phase du modèle référencé (Lenz, 2007), nous avons d’abord équilibré des bicouches lipidiques pendant environ deux millions d’étapes de Monte Carlo (MC) pour produire différentes phases pour le but de ce travail, voir la figure 2. Dans les unités réduites, ϵ/kB pour la température T et ϵ/σLJ3 pour la pression P, les variables thermodynamiques correspondantes sont : P = 2 et T = 1,08 pour la phase gel, P = 1 et T = 1,3 pour la phase fluide, P = 0,5 et T = 1,16 pour la phase interdigitée. Les paramètres caractéristiques des différentes phases, notamment la longueur moyenne des chaînes l¯, l’épaisseur de la bicouche d, la surface par lipide A et le paramètre d’ordre des chaînes Sz, sont résumés dans le tableau 2.

Figure 2. Instantanés de la membrane lipidique simulée dans la phase (A) gel, (B) fluide et (C) interdigitée. Les billes de tête et de queue du lipide sont représentées en rouge et en vert, respectivement.
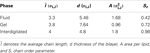
Tableau 2. Paramètres caractéristiques des bicouches lipidiques.
Des simulations ont été réalisées dans des conditions de température et de pression constantes (ensemble NPT) pour des bicouches lipidiques de différentes tailles. Pour étudier le spectre de puissance des fluctuations de hauteur des surfaces, nous avons simulé une bicouche dont les feuillets supérieur et inférieur sont constitués de 64 × 64 molécules lipidiques. Environ 17000-72000 billes ont été choisies pour le modèle de solvant (le nombre précis dépend de la phase simulée). Pour effectuer l’analyse du coefficient de Poisson, nous avons équilibré des bicouches rectangulaires composées de 12 × 24 molécules lipidiques par feuillet à trois phases différentes.
Pour déterminer à la fois E et ν, nous devons déterminer une de ces constantes élastiques séparément. En utilisant les conditions limites périodiques, nous introduisons une méthode pour calculer le coefficient de Poisson pour la surface (Abedpour et al., 2010). Le coefficient de Poisson est le rapport négatif des changements de déformation transversale divisés par les changements de déformation axiale dans un corps lorsqu’il est étiré ou comprimé dans la direction axiale sous une tension inférieure à la limite proportionnelle. Pour les déformations diagonales infinitésimales, le coefficient de Poisson peut être remplacé par le rapport des variations de longueur relatives sous la forme νij = -ΔLi/ηjLi, où ηj ≡ ΔLj/Lj est défini comme la fraction de la variation de longueur axiale. Ici, i ≠ j et i = x, y et z. Dans la méthode que nous présentons ici, la longueur entre les lipides voisins est redimensionnée par un facteur de (1 + η) dans la direction axiale, disons dans la direction y, et la modification ultérieure de la taille de la boîte de simulation dans les directions perpendiculaires, dans ce cas dans les directions x et z, est contrôlée. Tout en maintenant constante la longueur de la boîte réévaluée (1 + η) Ly, pour fixer la pression dans les simulations, les dimensions de la boîte sont maintenant autorisées à fluctuer uniquement dans les directions x et z. Lorsque les longueurs moyennes initiales dans les directions x et z étaient Lx et Lz, de nouvelles valeurs moyennes de Lx + ΔLx et Lz + ΔLz sont atteintes après la remise à l’échelle, en rééquilibrant le système pour un petit nombre de pas MC, voir la figure 3.

Figure 3. Instantanés de la membrane lipidique en phase fluide comme (A) configuration initiale, (B) après avoir augmenté la taille de la bicouche dans la direction y par un facteur de (1 + η), et (C) la bicouche relaxée fixant la taille de la membrane dans la direction y et variable dans la direction x. En conséquence d’un coefficient de Poisson positif pour la bicouche dans cette phase, la taille de la membrane dans la direction x est réduite et équilibrée après un petit nombre d’étapes de MC. Les perles de tête et de queue du lipide sont représentées en rouge et en vert, respectivement.
Pendant la simulation, pour accélérer la procédure de thermalisation après avoir étendu la boîte le long de la direction axiale, nous avons légèrement augmenté la température dans le système, ce qui a pour résultat de produire la plus grande mobilité pour les particules. Pour la phase fluide, nous avons fixé la température initiale à T = 1,3, puis nous l’avons modifiée à T = 1,4 pendant environ 400 étapes supplémentaires, avant de revenir à la valeur initiale. De même, pour les phases gel et interdigitée, les températures initiales étaient T = 1,08 et T = 1,16 et ont été commutées à T = 1,2 et T = 1,3, respectivement.
Une analyse courante des propriétés élastiques d’une membrane repose sur le Hamiltonien de Helfrich (Helfrich, 1973), qui décrit le coût de l’enthalpie libre élastique associé aux fluctuations de la hauteur de la membrane (écarts par rapport à la surface plane). Lorsque l’on paramètre la membrane en coordonnées cartésiennes (x,y) →(x,y,h(x,y)) (jauge de Monge), l’hamiltonien de Helfrich est, pour de petites fluctuations, donné par
où kc est la rigidité en flexion et σ est la tension superficielle. L’équation (4) est appliquée lorsque la membrane est considérée comme un corps d’épaisseur nulle. Une théorie élastique généralisée pour les membranes avec des épaisseurs finies a été suggérée par Brannigan et Brown (2006) et appliquée au modèle de Lenz-Schmid récemment (West et al., 2009 ; Neder et al…,
Pour déterminer h(x, y) à partir des simulations, nous avons discrétisé le plan (x, y) en une grille régulière avec un espacement de 2σLJ, déterminé dans chaque cellule (i, j) les coordonnées z moyennes z+(i, j) et z-(i, j) des perles de tête dans le feuillet supérieur et inférieur, respectivement, et calculé la hauteur h(i, j) – /2 (la moyenne h¯ a été soustraite par la suite). Pour une membrane de taille latérale L × L, Eq. (4) prédit :
pour le spectre de puissance des fluctuations, où ĥ(q) est la transformée de Fourier de h(x, y) au vecteur d’onde q, q = |q|, et <> désigne une moyenne d’équilibre. Dans le numérique, ĥ(q) est calculé à partir d’une transformée de Fourier discrète de h(i, j). Il est clair que l’équation (5) ne peut être vraie que pour une plage q 2π/L ≪ q ≪ 2π/σLJ, où ni la taille finie du système ni la taille (atomistique) des billes n’affectent les fluctuations. La gamme q correspondante pour les tailles de système accessibles dans un temps de calcul raisonnable n’est malheureusement pas grande, mais les ajustements de < |ĥ(q)|2 > ∕kBTL2 en fonction de q2 dans une gamme 0.5 ≤ q2 ≤ 1 donnent un bon accord avec l’équation (5) pour nos grandeurs.
Résultats et discussions
Dans le tableau 3, les rapports de Poisson obtenus νyx, νzx, et νxy ainsi que νzy pour différentes phases sont résumés. Comme le montre la figure 4, le coefficient de Poisson obtenu de cette manière est indépendant du facteur de remise à l’échelle η tant que η n’est ni trop grand, ce qui conduit à détruire la structure de la membrane, ni trop petit, ce qui ne dose pas assez d’espace libre pour le déplacement des particules. D’après le tableau 3 et la figure 4, les phases fluide et interdigitée ont le même coefficient de Poisson mesuré pour les directions x et y. Cela signifie que ces deux phases sont identiques. Cela signifie que ces deux phases sont isotropes dans le plan de la bicouche. En revanche, ce n’est plus le cas pour la phase gel. Les mesures montrent que, une bicouche en phase gel se comporte comme un matériau anisotrope, qui a deux valeurs distinctement différentes pour les deux directions différentes dans le plan de la bicouche.

Tableau 3. Constantes élastiques obtenues à partir de simulations de membranes lipidiques dans différentes phases.

Figure 4. Relaxation de -ΔLi/ηjLi en (A) phase fluide, (B) phase interdigitée et (C) phase gel. La valeur de plateau atteinte après environ 5000 pas MC, indépendante de la valeur de η, donne le coefficient de Poisson ν. Dans la phase gel, le coefficient de Poisson a des valeurs différentes pour νxy et νyx et cette phase agissant comme une surface anisotrope.
À l’inverse, lorsque la bicouche a été étendue dans la direction perpendiculaire au plan d’inclinaison, les lipides se réorganisent de telle sorte que la bicouche se rétrécit latéralement. Pour le présent travail, les longueurs de liaison des lipides dans la direction z (perpendiculaire au plan de la bicouche) n’ont pas été réévaluées. La raison en est que, pour observer l’effet de Poisson, la longueur entre les billes doit être rééchelonnée par un facteur, ce qui produit suffisamment d’espace pour que les particules puissent se réarranger. Cependant, dans la direction z, cette augmentation devrait se produire entre les billes liées à l’intérieur d’un lipide, ce qui provoque une rupture de liaison. Les valeurs rapportées pour νzx et νzy sont les changements de longueur relative résultants dans la longueur moyenne de la bicouche en raison de l’extension latérale des bicouches dans la direction x et y, respectivement.
Les valeurs obtenues pour la rigidité de flexion kc sont 5,2ϵ pour la phase fluide, et 7,6ϵ pour la phase interdigitée. Pour les phases gel et fluide, les résultats sont en accord avec les précédents rapports de calcul (West, 2008 ; West et al., 2009) et les résultats expérimentaux (Falcioni et al., 1997 ; Liu et Zhang, 2009). La densité spectrale pour la phase interdigitée a été calculée selon la même méthode. Nous rapportons ici la rigidité à la flexion pour la phase interdigitée. La figure 5 illustre les spectres de fluctuation de la hauteur pour les trois phases étudiées et les ajustements à l’Eq. (5).
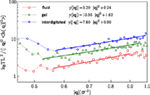
Figure 5. Spectres de fluctuation pour les phases fluide, gel et interdigitée et ajustements à l’Eq. (5).
Dans la théorie de l’élasticité bidimensionnelle, la rigidité en flexion kc est liée au coefficient de Poisson ν et au module d’Young E selon (Landau et al, 1986)
où d est l’épaisseur moyenne de la membrane, pour laquelle on obtient, 5,48σLJ, et 4,86σLJ pour le fluide, et les phases interdigitées, respectivement. En substituant les valeurs fondées pour les coefficients de Poisson et les rigidités de flexion pour les bicouches dans deux phases isotropes dans l’équation (6), on peut obtenir les modules d’Young correspondants. Les modules d’Young ainsi calculés sont de 0,28 et 0,67 en unités de ϵ/σ3 pour les états fluide et interdigité, respectivement. Évidemment, l’anisotropie observée dans la dose de gel ne permet pas d’utiliser le théorème ci-dessus pour la bicouche dans cette phase.
L’approche présentée dans cet article pourrait être appliquée aux membranes avec des compositions lipidiques plus complexes, étant donné que les modèles d’interaction vérifiés expérimentalement existent pour ces lipides. L’approche pourrait également être combinée avec une simulation plus précise des bicouches. Les simulations atomistiques complètes, et en particulier les simulations ab initio, pourraient en principe fournir des descriptions plus précises du système, mais s’accompagnent d’une énorme charge de calcul (Mashaghi et al., 2012, 2013a).
Conclusion
Nous avons réalisé des simulations Monte Carlo du modèle de bicouche lipidique à gros grains pour mieux comprendre les propriétés mécaniques des membranes lipidiques planes. En utilisant une méthode de remise à l’échelle, nous avons pu déterminer le coefficient de Poisson ν pour différentes phases, en plus de la rigidité en flexion déterminée à partir d’une analyse des fluctuations de la hauteur de la membrane basée sur le Hamiltonien de Helfrich. Cela nous permet de calculer également le module d’Young E pour différentes phases. Cette approche est précise, facile à mettre en œuvre et peut être appliquée à d’autres membranes telles que le graphène (Abedpour et al., 2010), afin de prédire la dépendance en température de son coefficient de Poisson et de son module d’Young. D’autres systèmes intéressants à étudier sont les nanofils métalliques cristallins où le module élastique contrôle leur performance structurelle et leur comportement fonctionnel tel que leur fréquence de résonance sous une charge oscillatoire typiquement appliquée pendant l’actionnement et la détection (Chen et al., 2006 ; McDowell et al, 2008).
Déclaration de conflit d’intérêts
Les auteurs déclarent que la recherche a été menée en l’absence de toute relation commerciale ou financière pouvant être interprétée comme un conflit d’intérêts potentiel.
Remerciements
Nous tenons à remercier Philipp Maass pour ses discussions utiles.
Abedpour, N, Asgari, R., et Tabar, M. R. R. (2010). Irréversibilité en réponse aux forces agissant sur les feuilles de graphène. Phys. Rev. Lett. 104, 196804. doi:10.1103/PhysRevLett.104.196804
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Ayton, G., Smondyrev, A., Bardenhagen, S., McMurtry, P., et Voth, G. (2002). Calcul du module de masse pour une bicouche lipidique avec une simulation de dynamique moléculaire sans équilibre. Biophys. J. 82, 1226-1238. doi:10.1016/S0006-3495(02)75479-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Brannigan, G., et Brown, F. L. H. (2006). Un modèle cohérent pour les fluctuations thermiques et les déformations induites par les protéines dans les bicouches lipidiques. Biophys. J. 90, 1501. doi:10.1529/biophysj.105.075838
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chen, C., Shi, Y., Zhang, Y., Zhu, J., and Yan, Y. (2006). Size dependence of Young’s modulus in ZnO nanowires. Phys. Rev. Lett. 96, 075505. doi:10.1103/PhysRevLett.96.075505
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Chernomordik, L. V., et Kozlov, M. M. (2008). Mécanique de la fusion des membranes. Nat. Struct. Mol. Biol. 15, 675-683. doi:10.1038/nsmb.1455
CrossRef Full Text
Claesson, M., Frost, R., Svedhem, S., and Andersson, M. (2011). Bicouches lipidiques couvrant les pores sur de la silice mésoporeuse dont la taille des pores varie. Langmuir 27, 8974-8982. doi:10.1021/la201411b
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Falcioni, M., Bowick, M. J., Guitter, E., et Thorleifsson, G. (1997). Le coefficient de Poisson des surfaces cristallines. Europhys. Lett. 38, 67-72. doi:10.1016/j.jhazmat.2010.12.101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Goetz, R., et Lipowsky, R. (1998). Simulations par ordinateur de membranes bicouches : auto-assemblage et tension interfaciale. J. Chem. Phys. 108, 7397-7409. doi:10.1063/1.476160
CrossRef Full Text
Grest, G. S., et Kremer, K. (1986). Simulation de la dynamique moléculaire pour les polymères en présence d’un bain de chaleur. Phys. Rev. A 33, 3628-3631. doi:10.1103/PhysRevA.33.3628
CrossRef Full Text
Hall, L., Coluci, V., Galvao, D., Kozlov, M., Zhang, M., Dantas, S., et al. (2008). Sign change of Poisson’s ratio for carbon nanotube sheets. Science 320, 504-507. doi:10.1126/science.1149815
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Helfrich, W. (1973). Propriétés élastiques des bicouches lipidiques – théorie et expériences possibles. Z. Naturforsch. C 28, 693.
Illya, G., Lipowsky, R., et Shillcock, J. C. (2005). Effet de la longueur de la chaîne et de l’asymétrie sur les propriétés matérielles des membranes bicouches. J. Chem. Phys. 122, 1-6. doi:10.1063/1.1917794
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Jeon, J., et Voth, G. (2005). Les réponses dynamiques de contrainte au changement de zone dans les membranes bicouches lipidiques planes. Biophys. J. 88, 1104-1119. doi:10.1529/biophysj.104.052183
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Landau, L. D., Pitaevskii, L. P., Lifshitz, E. M., and Kosevich, A. M. (1986). Theory of Elasticity, Volume 7, 3rd Edn. Oxford : Butterworth-Heinemann.
Lenz, O. (2007). Simulation par ordinateur des bicouches lipidiques. Thèse de doctorat, Université de Bielefeld, Bielefeld.
Lenz, O., et Schmid, F. (2005). Un modèle informatique simple pour les bicouches lipidiques liquides. J. Mol. Liq. 117, 147-152. doi:10.1016/j.molliq.2004.08.008
CrossRef Full Text
Lindahl, E., et Edholm, O. (2001). Simulation par dynamique moléculaire des taux de relaxation RMN et de la dynamique lente dans les bicouches lipidiques. J. Chem. Phys. 115, 4938-4950. doi:10.1529/biophysj.107.121806
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Liu, P., et Zhang, Y. W. (2009). Rigidité de flexion du graphène en fonction de la température. Appl. Phys. Lett. 94, 231912. doi:10.1063/1.3155197
CrossRef Full Text
Martins, B., et Galvao, D. (2010). Nanorubans de graphène incurvés : structure et dynamique des nanobelts de carbone. Nanotechnology 21, 075710. doi:10.1088/0957-4484/21/7/075710
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Martins, P., Malhaire, C., Brida, S., et Barbier, D. (2009). Sur la détermination du coefficient de Poisson de films épais submicroniques monocouches et bicouches sous contrainte. Microsyst. Technol. 15, 1343-1348. doi:10.1007/s00542-009-0822-5
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Nafari, N., Esfarjani, K., Maass, P., et al. (2012). L’eau interfaciale facilite le transfert d’énergie en induisant des vibrations étendues dans les lipides membranaires. J. Phys. Chem. B 116, 6455-6460. doi:10.1021/jp302478a
CrossRef Full Text
Mashaghi, A., Partovi-Azar, P., Jadidi, T., Anvari, M., Panahian, J. S., Nafari, N., et al. (2013a). Amélioration de l’autoionisation de l’eau aux interfaces des phospholipides. J. Phys. Chem. C 117, 510-514. doi:10.1021/jp3119617
CrossRef Full Text
Mashaghi, S., Jadidi, T., Koenderink, G., et Mashaghi, A. (2013b). La nanotechnologie des lipides. Int. J. Mol. Sci. 14, 4242-4282. doi:10.3390/ijms14024242
CrossRef Full Text
McDowell, M., Leach, A. et Gall, K. (2008). Sur le module élastique des nanofils métalliques. Nano Lett. 8, 3613-3618. doi:10.1021/nl801526c
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Mitchell, J. S., Zorman, C. A., Kicher, T., Roy, S., et Mehregany, M. (2003). Examination of bulge test for determining residual stress, Young’s modulus, and Poisson’s ratio of 3c-sic thin films. J. Aerosp. Eng. 16, 46-54. doi:10.1061/(ASCE)0893-1321(2003)16:2(46)
CrossRef Full Text
Morone, N., Fujiwara, T., Murase, K., Kasai, R. S., Ike, H., Yuasa, S., et al. (2006). Reconstruction tridimensionnelle du squelette de la membrane à l’interface de la membrane plasmique par tomographie électronique. J. Cell Biol. 174, 851-862. doi:10.1083/jcb.200606007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Nagle, J. F., et Tristram-Nagle, S. (2000). Structure of lipid bilayers. Biochim. Biophys. Acta 1469, 159-195. doi:10.1016/S0304-4157(00)00016-2
CrossRef Full Text
Neder, J., West, B., Nielaba, P., et Schmid, F. (2010). Simulations à gros grains de membranes sous tension. J. Chem. Phys. 132, 115101. doi:10.1063/1.3352583
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Popescu, G., Ikeda, T., Goda, K., Best-Popescu, C. A., Laposata, M., Manley, S., et al. (2006). Optical measurement of cell membrane tension. Phys. Rev. Lett. 97, 218101. doi:10.1103/PhysRevLett.97.218101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Sansom, D. M. S. P., et Biggin, P. C. (2010). Simulations moléculaires et biomembranes : From Biophysics to Function, 1st Edn. Cambridge, UK : Royal Society of Chemistry.
Schmidt, D., et MacKinnon, R. (2008). Le gating du canal k+ dépendant de la tension et la sensibilité à la toxine du capteur de tension dépendent de l’état mécanique de la membrane lipidique. Proc. Natl. Acad. Sci. U.S.A. 105, 19276-19281. doi:10.1073/pnas.0810187105.
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Seto, H., Yamada, N., Nagao, M., Hishida, M., et Takeda, T. (2008). Module de flexion des bicouches lipidiques dans une phase liquide-cristalline incluant un régime de gonflement anormal estimé par des expériences d’écho de spin neutronique. Eur. Phys. J. E Soft Matter 26, 217-223. doi:10.1140/epje/i2007-10315-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
Thakkar, F. M., Maiti, P., Kumarana, V., and Ayappa, K. (2011). Vérification des mises à l’échelle de la rigidité à la flexion des membranes bicouches à l’aide de modèles à méso-échelle. Soft Matter 7, 3963-3966. doi:10.1039/c0sm00876a
CrossRef Full Text
Tierney, K. J., Block, D. E., and Longo, M. L. (2005). Elasticité et comportement de phase de la membrane DPPC modulée par le cholestérol, l’ergostérol et l’éthanol. Biophys. J. 89, 2481-2493. doi:10.1529/biophysj.104.057943
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text
West, B. (2008). Interactions lipides-protéines dans les membranes lipidiques. Thèse de doctorat, Université de Bielefeld, Bielefeld.
West, B., Brown, F. L. H., et Schmid, F. (2009). Interactions membrane-protéine dans un modèle générique à gros grains pour les bicouches lipidiques. Biophys. J. 96, 101. doi:10.1529/biophysj.108.138677
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text