Ayant défini que, la fonction logarithmique y = log b x est la fonction inverse de la fonction exponentielle y = b x. Nous pouvons maintenant procéder à la représentation graphique des fonctions logarithmiques en examinant la relation entre les fonctions exponentielles et logarithmiques.
Mais avant de sauter dans le sujet de la représentation graphique des fonctions logarithmiques, il est important que nous nous familiarisions avec les termes suivants :
- Le domaine d’une fonction
Le domaine d’une fonction est un ensemble de valeurs que vous pouvez substituer dans la fonction pour obtenir une réponse acceptable.
- L’étendue d’une fonction
C’est l’ensemble des valeurs que vous obtenez après avoir substitué les valeurs du domaine à la variable.
- Asymptotes
Il existe trois types d’asymptotes, à savoir ; verticale, horizontale et oblique. L’asymptote verticale est la valeur de x où la fonction croît sans limite à proximité.
Les asymptotes horizontales sont des valeurs constantes que f(x) approche lorsque x croît sans limite. Les asymptotes obliques sont des polynômes du premier degré dont f(x) se rapproche au fur et à mesure que x croît sans limite.
Comment tracer le graphique des fonctions logarithmiques ?
Le graphique d’une fonction logarithmique peut être réalisé en examinant le graphique de la fonction exponentielle, puis en échangeant x et y.
Le graphique d’une fonction exponentielle f (x) = b x ou y = b x contient les caractéristiques suivantes :
- Le domaine d’une fonction exponentielle est constitué de nombres réels (-infini, infini).
- L’étendue est également constituée de nombres réels positifs (0, infini)
- Le graphique d’une fonction exponentielle passe normalement par le point (0, 1). Cela signifie que l’ordonnée à l’origine est au point (0, 1).
- Le graphique d’une fonction exponentielle f(x) = b x a une asymptote horizontale à y = 0.
- Un graphique exponentiel diminue de gauche à droite si 0 < b < 1, et ce cas est appelé décroissance exponentielle.
- Si la base de la fonction f(x) = b x est supérieure à 1, alors son graphique augmente de gauche à droite et est appelé croissance exponentielle.
En examinant les caractéristiques ci-dessus une par une, nous pouvons de la même manière déduire les caractéristiques des fonctions logarithmiques comme suit :
- Une fonction logarithmique aura pour domaine (0, infini).
- L’étendue d’une fonction logarithmique est (-infini, infini).
- Le graphique de la fonction logarithmique passe par le point (1, 0), qui est l’inverse de (0, 1) pour une fonction exponentielle.
- Le graphique d’une fonction logarithmique possède une asymptote verticale en x = 0.
- Le graphique d’une fonction logarithmique décroît de gauche à droite si 0 < b < 1.
- Et si la base de la fonction est supérieure à 1, b > 1, alors le graphique augmentera de gauche à droite.
Comment représenter graphiquement une fonction logarithmique de base ?
Une fonction logarithmique de base est généralement une fonction sans décalage horizontal ou vertical.
Voici les étapes pour créer le graphique d’une fonction logarithmique de base.
- Puisque toutes les fonctions logarithmiques passent par le point (1, 0), on repère et on place un point au point.
- Pour éviter que la courbe ne touche l’axe des y, nous traçons une asymptote à x = 0.
- Si la base de la fonction est supérieure à 1, augmentez votre courbe de gauche à droite. De même, si la base est inférieure à 1, diminuez votre courbe de gauche à droite.
Voyons maintenant les exemples suivants :
Exemple 1
Graphiez la fonction logarithmique f(x) = log 2 x et indiquez l’étendue et le domaine de la fonction.
Solution
- Evidemment, une fonction logarithmique doit avoir pour domaine et étendue (0, infini) et (-infini, infini)
- Puisque la fonction f(x) = log 2 x est supérieure à 1, nous allons augmenter notre courbe de gauche à droite, a montré ci-dessous.
- Nous ne pouvons pas voir l’asymptote verticale à x = 0 car elle est cachée par l’axe des y.
Exemple 2
Dessinez un graphique de y = log 0,5 x
Solution
- Placez un point au point (1, 0). Toutes les courbes logarithmiques passent par ce point.
- Dessinez une asymptote en x = 0.
- Puisque la base de la fonction y = log 5 x est inférieure à 1, nous allons diminuer notre courbe de gauche à droite.
- La fonction y = log 5 x aura également (0, infini) et (-infini, infini) comme domaine et étendue.
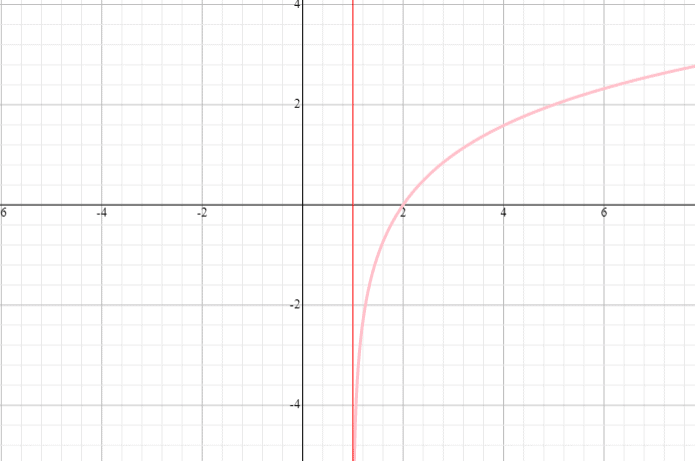
Graphie d’une fonction logarithmique avec un décalage horizontal
Les fonctions logarithmiques avec un décalage horizontal sont de la forme f(x) = log b (x + h) ou f (x) = log b (x – h), où h = le décalage horizontal. Le signe du décalage horizontal détermine la direction du décalage. Si le signe est positif, le décalage sera négatif, et si le signe est négatif, le décalage devient positif.
En appliquant le décalage horizontal, les caractéristiques d’une fonction logarithmique sont affectées de la manière suivante :
- L’interception x – se déplace vers la gauche ou la droite d’une distance fixe égale à h.
- L’asymptote verticale se déplace d’une distance égale à h.
- Le domaine de la fonction change également.
Exemple 3
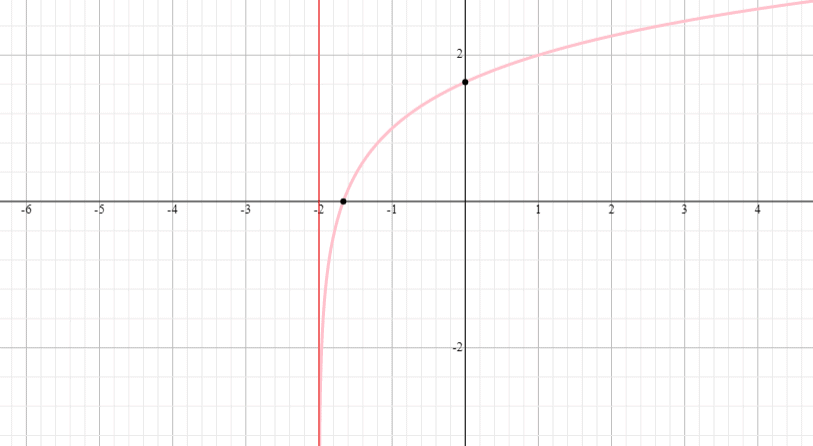
Dessinez un graphique de la fonction f(x) = log 2 (x + 1) et indiquez le domaine et l’étendue de la fonction.
Solution
⟹ Domaine : (- 1, infini)
⟹ Domaine : (-infini, infini)
Exemple 4
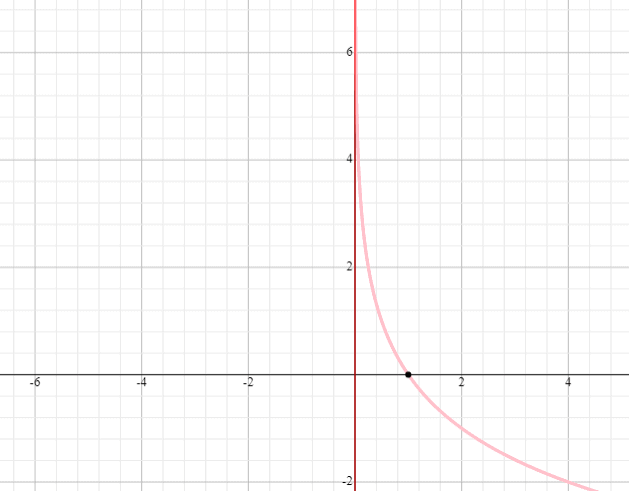
Graphiez y = log 0,5 (x – 1) et indiquez le domaine et l’étendue.
Solution
⟹ Domaine : (1, infini)
⟹ Domaine : (-infini, infini)
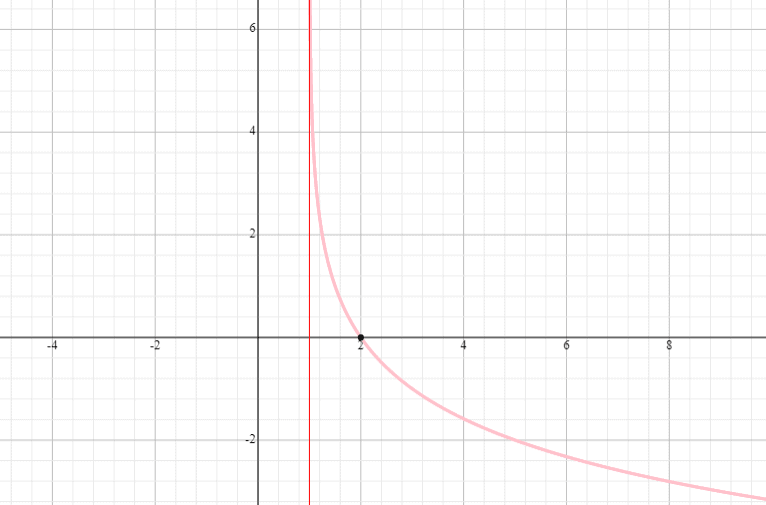
Comment représenter graphiquement une fonction avec une verticale ?
Une fonction logarithmique avec un décalage horizontal et vertical est de la forme f(x) = log b (x) + k, où k = le décalage vertical.
Le décalage vertical affecte les caractéristiques d’une fonction comme suit :
- L’ordonnée à l’origine des x se déplacera soit vers le haut, soit vers le bas avec une distance fixe de k
Exemple 5
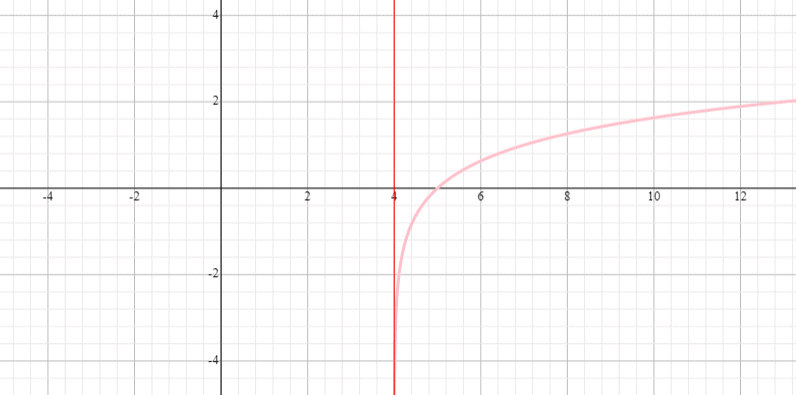
Graphiez la fonction y = log 3 (x – 4) et indiquez l’étendue et le domaine de la fonction.
Solution
⟹ Domaine : (0, infini)
⟹ Domaine : (-infini, infini)
Fonctions à décalage horizontal et vertical
Une fonction logarithmique à décalage horizontal et vertical est de la forme (x) = log b (x + h) + k, où k et h sont respectivement les décalages vertical et horizontal.
Exemple 6
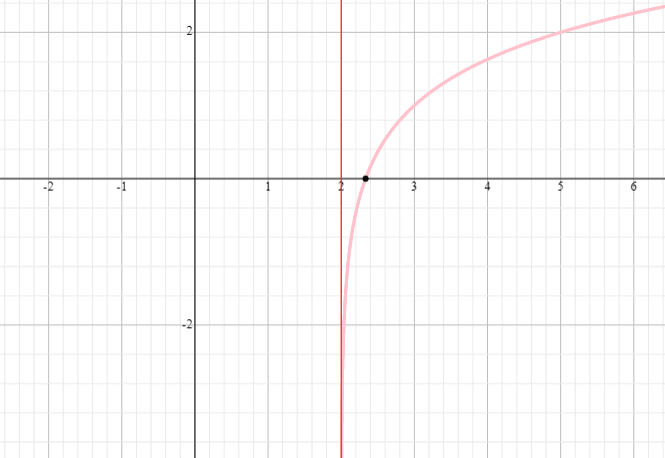
Graphiez la fonction logarithmique y = log 3 (x – 2) + 1 et trouvez le domaine et l’étendue de la fonction.
Solution
⟹ Domaine : (2,infini)
⟹ Domaine : (-infini, infini)
Exemple 7
Graphier la fonction logarithmique y = log 3 (x + 2) + 1 et trouver le domaine et l’étendue de la fonction.
Solution
⟹ Domaine : (- 2,infini)
⟹ Domaine : (-infini, infini)