Régression Probit
Dans la régression Probit, la fonction de distribution normale standard cumulative \(\Phi(\cdot)\) est utilisée pour modéliser la fonction de régression lorsque la variable dépendante est binaire, c’est-à-dire que nous supposons que\
\(\beta_0 + \beta_1 X\) dans (11.4) joue le rôle d’un quantile \(z\). Rappelez-vous que \ tel que le coefficient Probit \(\beta_1\) dans (11. 4) est le changement de \(z\) associé à un changement d’une unité de \(X\). Bien que l’effet sur \(z\) d’un changement de \(X\) soit linéaire, le lien entre \(z\) et la variable dépendante \(Y\) est non linéaire puisque \(\Phi\) est une fonction non linéaire de \(X\).
Puisque la variable dépendante est une fonction non linéaire des régresseurs, le coefficient sur \(X\) n’a pas d’interprétation simple. Selon le concept clé 8.1, la modification attendue de la probabilité que \(Y=1\) due à une modification de \(P/I \ ratio\) peut être calculée comme suit:
- Calculer la probabilité prédite que \(Y=1\) pour la valeur initiale de \(X\).
- Calculer la probabilité prédite que \(Y=1\) pour \(X + \Delta X\).
- Calculer la différence entre les deux probabilités prédites.
Bien sûr, nous pouvons généraliser (11.4) à la régression Probit avec des régresseurs multiples pour atténuer le risque de faire face à un biais de variable omise. Les éléments essentiels de la régression Probit sont résumés dans le concept clé 11.2.
Modèle Probit, probabilités prédites et effets estimés
Supposons que \(Y\) soit une variable binaire. Le modèle
\with\ est le modèle Probit de population avec plusieurs régresseurs \(X_1, X_2, \cdot, X_k\) et \(\Phi(\cdot)\) est la fonction de distribution normale standard cumulative.
La probabilité prédite que \(Y=1\) étant donné \(X_1, X_2, \dots, X_k\) peut être calculée en deux étapes :
-
Calculer \(z = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k\)
-
Rechercher \(\Phi(z)\) en appelant pnorm().
\(\beta_j\) est l’effet sur \(z\) d’une variation d’une unité du régresseur \(X_j\), en maintenant constants tous les autres \(k-1\) régresseurs.
L’effet sur la probabilité prédite d’un changement dans un régresseur peut être calculé comme dans le concept clé 8.1.
En R, les modèles Probit peuvent être estimés à l’aide de la fonction glm() du package stats. En utilisant l’argument famille, nous spécifions que nous voulons utiliser une fonction de liaison Probit.
Nous estimons maintenant un modèle Probit simple de la probabilité d’un refus de prêt hypothécaire.
# estimate the simple probit modeldenyprobit <- glm(deny ~ pirat, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.19415 0.18901 -11.6087 < 2.2e-16 ***#> pirat 2.96787 0.53698 5.5269 3.259e-08 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Le modèle estimé est
Tout comme dans le modèle de probabilité linéaire, nous constatons que la relation entre la probabilité de refus et le ratio paiements/revenus est positive et que le coefficient correspondant est hautement significatif.
Le morceau de code suivant reproduit la figure 11.2 du livre.
# plot dataplot(x = HMDA$pirat, y = HMDA$deny, main = "Probit Model of the Probability of Denial, Given P/I Ratio", xlab = "P/I ratio", ylab = "Deny", pch = 20, ylim = c(-0.4, 1.4), cex.main = 0.85)# add horizontal dashed lines and textabline(h = 1, lty = 2, col = "darkred")abline(h = 0, lty = 2, col = "darkred")text(2.5, 0.9, cex = 0.8, "Mortgage denied")text(2.5, -0.1, cex= 0.8, "Mortgage approved")# add estimated regression linex <- seq(0, 3, 0.01)y <- predict(denyprobit, list(pirat = x), type = "response")lines(x, y, lwd = 1.5, col = "steelblue")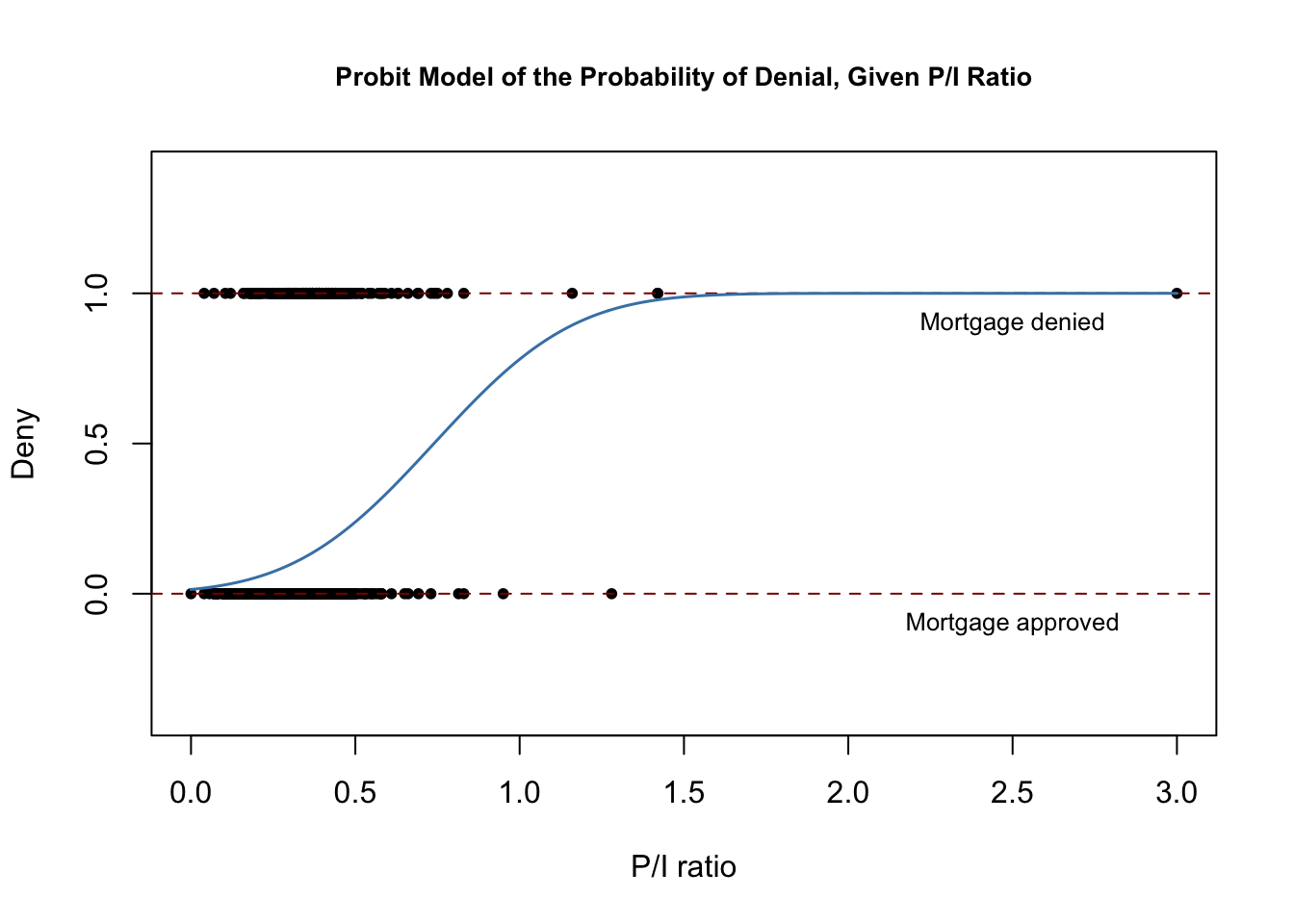
La fonction de régression estimée a une forme étirée en « S », ce qui est typique de la CDF d’une variable aléatoire continue avec une PDF symétrique comme celle d’une variable aléatoire normale. La fonction est clairement non linéaire et s’aplatit pour les grandes et petites valeurs de \(P/I \ ratio\). La forme fonctionnelle garantit donc également que les probabilités conditionnelles prédites d’un refus se situent entre \(0\) et \(1\).
Nous utilisons predict() pour calculer le changement prédit de la probabilité de refus lorsque \(P/I \ ratio\) est augmenté de \(0.3\) à \(0,4\).
# 1. compute predictions for P/I ratio = 0.3, 0.4predictions <- predict(denyprobit, newdata = data.frame("pirat" = c(0.3, 0.4)), type = "response")# 2. Compute difference in probabilitiesdiff(predictions)#> 2 #> 0.06081433Nous constatons qu’une augmentation du ratio paiement/revenu de \(0,3\) à \(0,4\) est prédite pour augmenter la probabilité de refus d’environ \(6.2\%\).
Nous poursuivons en utilisant un modèle Probit augmenté pour estimer l’effet de la race sur la probabilité de refus d’une demande de prêt hypothécaire.
denyprobit2 <- glm(deny ~ pirat + black, family = binomial(link = "probit"), data = HMDA)coeftest(denyprobit2, vcov. = vcovHC, type = "HC1")#> #> z test of coefficients:#> #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -2.258787 0.176608 -12.7898 < 2.2e-16 ***#> pirat 2.741779 0.497673 5.5092 3.605e-08 ***#> blackyes 0.708155 0.083091 8.5227 < 2.2e-16 ***#> ---#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1L’équation du modèle estimé est
Bien que tous les coefficients soient hautement significatifs, les coefficients estimés sur le ratio paiements/revenus et l’indicateur d’ascendance afro-américaine sont tous deux positifs. Encore une fois, les coefficients sont difficiles à interpréter mais ils indiquent que, premièrement, les Afro-Américains ont une probabilité de refus plus élevée que les demandeurs blancs, en maintenant constant le ratio paiements-revenus et, deuxièmement, les demandeurs ayant un ratio paiements-revenus élevé font face à un risque plus élevé d’être rejetés.
Quelle est l’importance de la différence estimée dans les probabilités de refus entre deux demandeurs hypothétiques ayant le même ratio paiements-revenus ? Comme précédemment, nous pouvons utiliser predict() pour calculer cette différence.
# 1. compute predictions for P/I ratio = 0.3predictions <- predict(denyprobit2, newdata = data.frame("black" = c("no", "yes"), "pirat" = c(0.3, 0.3)), type = "response")# 2. compute difference in probabilitiesdiff(predictions)#> 2 #> 0.1578117Dans ce cas, la différence estimée des probabilités de refus est d’environ \(15,8\%\).